P3830 隨機樹

坑題，別人的題解我看了一個下午沒一個看得懂的，我還是太弱了。

題目鏈接 P3830 [SHOI2012]隨機樹

題目描述

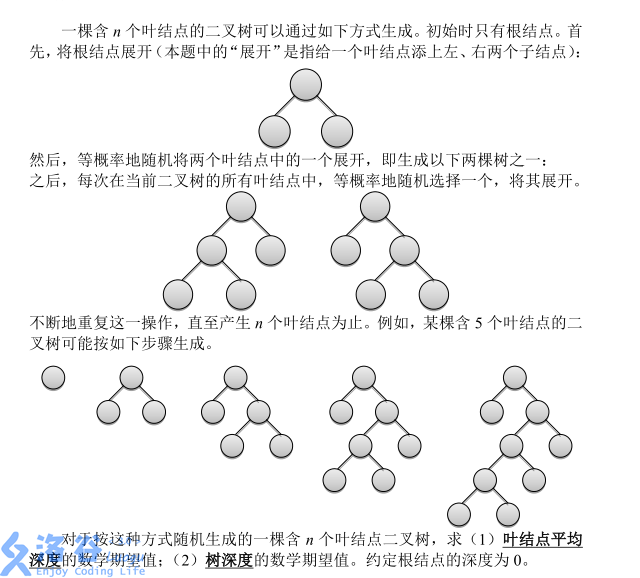
輸入輸出格式

輸入格式：

輸入僅有一行，包含兩個正整數 q, n，分別表示問題編號以及葉結點的個數。

輸出格式：

輸出僅有一行，包含一個實數 d，四舍五入精確到小數點後 6 位。如果 q = 1，則 d 表示葉結點平均深度的數學期望值；如果 q = 2，則 d 表示樹深度的數學期望值。

說明

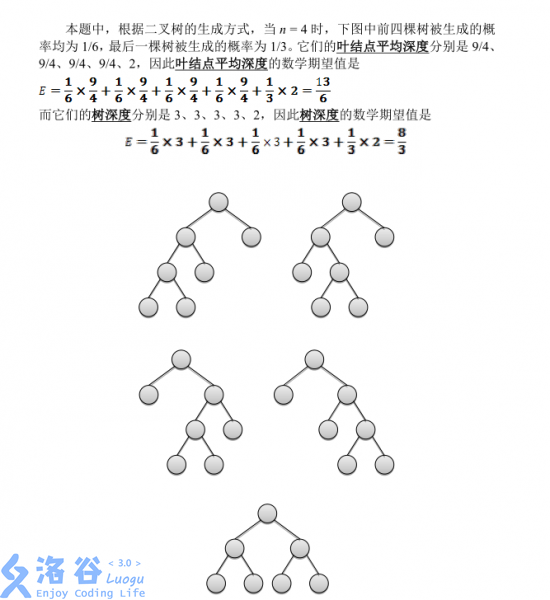
第一問很水，考慮每次新拓展節點就是讓樹的總深度加上 2

也就是: $$f[i]= \dfrac{f[i-1]*(i-1) + f[i-1] + 2 }{i}

意思就是原來 i-1 個節點的平均深度，乘上 (i-1) 變成深度和，然後再加一次 平均深度，然後加 2 ，除以 i 個葉子結點得到當前答案。

化簡後式子就變成了: $$f[i]=f[i-1] + \dfrac{2} {i} $$

然後來到第二問（關鍵問題）。

首先這是概率期望 dp ，於是我們考慮設計狀態。

那麽我們讓 $f[i][j]$ 表示 i 個葉子節點，深度為 j 的概率（是概率）。

那麽轉移就是： $$ f[i][j] = \dfrac{ f[k][j-1] + f[i-k][j-1]-f[k][j-1] \times f[i-k][j-1] } {i-1} $$

其中 f[i][j] 表示新樹狀態，f[k][j-1] 為左子樹狀態，f[i-k][j-1] 為右子樹狀態。

很多題解到這兒就沒了，就沒了！也不解釋一下的說（尤其 i-1 解釋的是真草率）。

最後我自己口胡了一下大概可能也許想通了。

首先 f[i][j] 是我們現在構造出的樹的狀態，也就是說我們用兩個子樹拼湊出了一棵新樹，而根是新加節點（新加節點會使得左右子樹所有葉子結點深度均增加 1 ）。

所以這點很重要，也是尤其關鍵的一步，在強調一遍，f[i][j] 只是代表了新樹的形態，且是已經確定了的形態。

那麽形成這棵樹的概率也就是上面的轉移式了，左子樹有 j-1 個節點的概率 + 右子樹有 j-1 個節點的概率 - 左右子樹同時有 j-1 個節點的概率（容斥）。

接著呢？ 我們考慮除去 i-1 的意義（自己的想法而已）：

我們讓當前的這棵樹回到上一個狀態，也就是說我們令這棵樹最後一次葉子結點的擴展取消，回到 i-1 的狀態。 （請腦補）

然後聰明的你已經想出來了，這時候要達到當前狀態的概率是？ 當然是 1/(i-1) 。因為當前這棵樹刪除的節點擴展回來的概率就是 1/(i-1)。

然後問題就解決了，放代碼（非常短啊）。

 1 //by Judge
 2 #include<iostream>
 3 #include<cstdio>
 4 using namespace std;
 5 int q,n; double ans,f[111][111];
 6 int main(){ scanf("%d%d",&q,&n);
 7     if(q==1){
 8         for(int i=2;i<=n;++i) ans+=2.0/i;
 9         return printf("%.6lf\n",ans),0;
10     } f[1][0]=f[2][1]=f[3][2]=1;
11     for(int i=4;i<=n;++i) for(int j=1;j<=n;++j)
12         for(int k=0;k<j;++k) for(int l=0;l<i-j;++l)
13             f[i][max(k,l)+1]+=(f[j][k]*f[i-j][l])/(i-1);
14     for(int i=1;i<n;++i) ans+=f[n][i]*i; return printf("%.6lf\n",ans),0;
15 }

P3830 [SHOI2012]隨機樹 題解