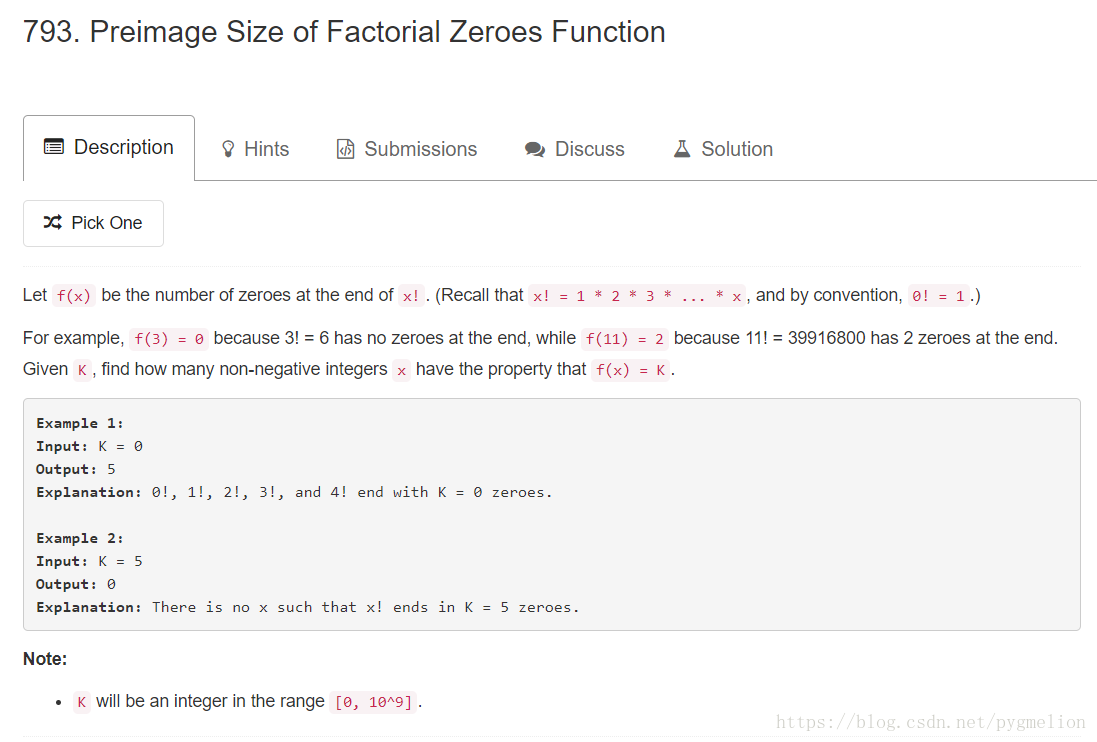
題目描述

這道題的題目名稱非常的難懂，但是讀了題目內容以後，就不難理解了，定義函式f(x)為x!的末尾0的個數，現在給了我們一個非負整數K，問使得f(x)=K成立的非負整數的個數。

問題分析

之前做過一道有關階乘末尾零的個數的題，從那道里知道了末尾0其實是由2和5相乘為10得到的，而階乘中2的數量遠多於5的個數，所以10的個數就只取決於5的個數。

需要注意的一點就是，像25，125，這樣的不只含有一個5的數字需要考慮進去。比如，24的階乘末尾有4個0，分別是5，10，15，20中的四個5組成的，而25的階乘末尾就有6個0，分別是5，10，15，20中的各一個5，還有25中的兩個5，所以共有六個5，那麼就不存在其階乘數末尾有5個0的數。

除此之外，我們知道20，21，22，23，24，這五個數的階乘數末尾零的個數其實是相同的，都是有4個，因為它們包含的5的個數相同。而19，18，17，16，15，這五個數末尾零個數相同，均為3。那麼我們其實可以發現，每五個數，必會至少多出1個5，有可能更多。所以階乘末尾零個數均為K個的x值，只有兩種情況，要麼是5，要麼是0。

演算法設計

演算法1

基於之前那道題的解法，我們有了如何快速求一個給定的數字階乘末尾零的個數，那麼我們只要找到了一個這樣的數，其階乘末尾零的個數等於K的話，那麼就說明總共有5個這樣的數，返回5，反之，如果找不到這樣的數字，就返回0。那麼像這種選一個candidate數字，再用二分搜尋進行驗證的操作。首先要確定二分搜尋法的範圍，左邊界為0，關鍵是來確定右邊界。

我們來分析一下，一個數字的階乘末尾零個數為K，那麼這個數字能有多大，就拿前面舉的例子來說吧，末尾有4個0的最大數字是24，有六個0的最大是29，那麼我們發現它們都不會超過5*(K+1)這個範圍，所以這就是我們的右邊界。然後進行二分搜尋法。

注意：右邊界可能會超過整型數範圍，所以要用長整型來表示。

class Solution {
public:
    int preimageSizeFZF(int K) {
        long left = 0, right = 5L * (K + 1);
        while (left < right) {
            long mid = left + (right - left) / 2;
            long cnt = numOfTrailingZeros(mid);
            if (cnt == K) return 5;
            else if (cnt < K) left = mid + 1;
            else right = mid;
        }
        return 0;
    }
    long numOfTrailingZeros(long x) {
        long res = 0;
        for (; x > 0; x /= 5) {
            res += x / 5;
        }
        return res;
    }
};
 

演算法2

在演算法1 的基礎上進行程式碼模組整合，將while迴圈柔和進去即可，程式碼減少了30%。

class Solution {
public:
    int preimageSizeFZF(int K) {
        long left = 0, right = 5L * (K + 1);
        while (left < right) {
            long mid = left + (right - left) / 2, cnt = 0;
            for (long i = 5; mid / i > 0; i *= 5) {
                cnt += mid / i;
            }
            if (cnt == K) return 5;
            else if (cnt < K) left = mid + 1;
            else right = mid;
        }
        return 0;
    }
};

演算法3

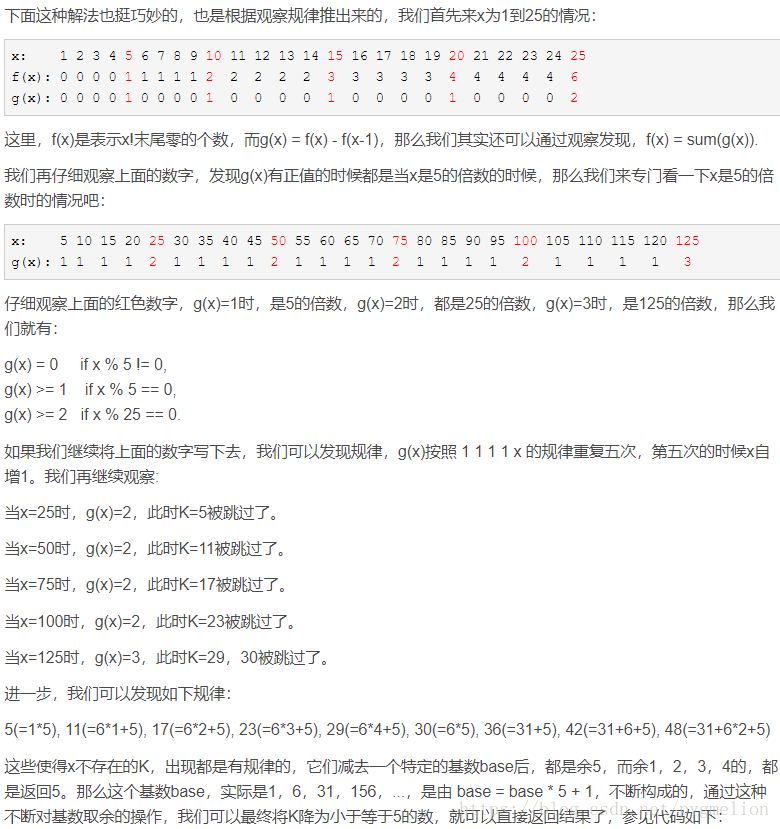
通過後續的資料查詢，我發現有博主通過規律尋找的方法，找出了其中蘊含的規律，順利解決該問題。不過我以為，這樣的解法不具有演算法設計的巧妙性，有一點運氣的程式在裡面。所以，我在這裡不做贅述，截圖供參考，豐富思維，同時，我也按照他的思路實現了他的演算法。

class Solution {
public:
    int preimageSizeFZF(int K) {
        if (K < 5) return 5;
        int base = 1;
        while (base * 5 + 1 <= K) {
            base = base * 5 + 1;
        }
        if (K / base == 5) return 0;
        return preimageSizeFZF(K % base);
    }
};