BZOJ1808: [Ioi2007]training 訓練路徑
阿新 • • 發佈:2018-11-02
題面
題意
給出一棵樹和幾條非樹邊,每條非樹邊有一個權值,表示去掉它的代價,樹邊不能被去掉,問若要讓圖中沒有偶環,至少要付出多少代價。
每個點的度數小於等於10
做法
首先與樹組成偶環的邊直接去掉,然後我們可以將非樹邊看作樹上兩點間的路徑,然後可以發現如果兩條路徑邊的交集非空,則這兩條非樹邊一定能與一些樹邊組成偶環。
然後問題就轉化為了:在一棵樹上有一些路徑,每條路徑有一個權值,從中選擇一些沒有邊重合的路徑,最大權值是多少。
因為每個點的度數小於等於10,因此我們可以用狀壓dp來做,記
表示在以
點為根節點的子樹中,
點的所有邊(除了向父節點連的邊)中不考慮邊集
內的邊所指向的子樹的最大權值。
然後考慮一條路徑對答案的貢獻,發現對於一條
為
的邊
,它會讓
少選兩條邊,貢獻為
鏈上除了
的所有點
鏈上的邊
該路徑的權值。
例:
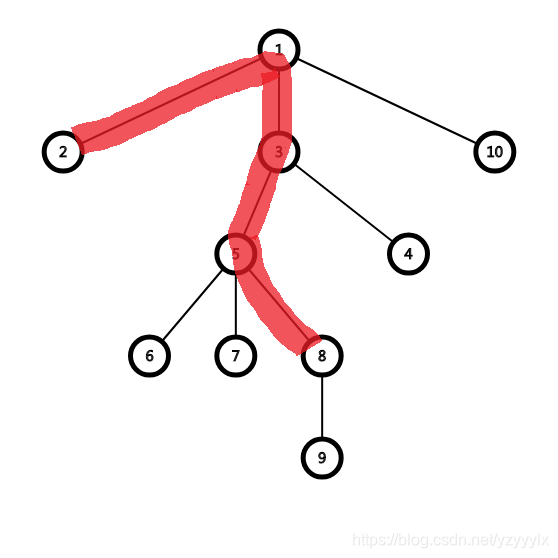
對於紅色的這條路徑,其貢獻為8的整棵子樹+5去掉8這棵子樹後的子樹+3去掉5這棵子樹後的子樹+1去掉2,3這兩棵子樹後的子樹+2的整棵子樹(雖然為空)。
程式碼
#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
#define P pair<int,int>
#define mp make_pair
#define fi first
#define se second
#define INF 0x3f3f3f3f
#define N 1100
#define M 5010
using namespace std;
int n,m,ans,ds[N],fa[N],deep[N],LCA[N][N],mx,a[M],b[M],c[M],dp[N][N],bh[N],tt;
vector<int>son[N],have[N];
inline void Max(int &u,int v){if(v>u) u=v;}
int lca(int u,int v)
{
if(u==v) return u;
if(deep[u]<deep[v]) swap(u,v);
if(LCA[u][v]) return LCA[u][v];
return LCA[u][v]=lca(fa[u],v);
}
void dfs(int now,int last)
{
int i,j,t,d=-1;
for(i=0; i<son[now].size(); i++)
{
t=son[now][i];
if(t==last)
{
d=i;
continue;
}
bh[t]=i-(d!=-1);
deep[t]=deep[now]+1;
fa[t]=now;
dfs(t,now);
}
if(d!=-1)
{
for(i=d;i<son[now].size()-1;i++) son[now][i]=son[now][i+1];
son[now].pop_back();
}
}
void Dfs(int now)
{
int i,j,p,q,o,sum,t,tmp;
for(i=0;i<son[now].size();i++) Dfs(son[now][i]);
for(i=0;i<(1 << son[now].size());i++)
{
sum=0;
for(j=0;j<son[now].size();j++)
{
if((1 << j)&i) continue;
sum+=dp[son[now][j]][0];
}
dp[now][i]=sum;
}
for(i=0;i<have[now].size();i++)
{
o=have[now][i];
sum=c[o];
p=a[o],q=b[o];
t=0;
if(p!=now)
{
sum+=dp[p][0];
for(;fa[p]!=now;p=fa[p]) sum+=dp[fa[p]][(1 << bh[p])];
t|=(1 << bh[p]);
}
if(q!=now)
{
sum+=dp[q][0];
for(;fa[q]!=now;q=fa[q]) sum+=dp[fa[q]][(1 << bh[q])];
t|=(1 << bh[q]);
}
tmp=(t^((1 << son[now].size())-1));
for(j=tmp;;j=(j-1)&tmp)
{
Max(dp[now][j],dp[now][j|t]+sum);
if(!j) break;
}
}
}
int main()
{
int i,j,p,q,o,l,t;
cin>>n>>m;
for(i=1; i<=m; i++)
{
scanf("%d%d%d",&p,&q,&o);
if(!o)
{
son[p].push_back(q);
son[q].push_back(p);
ds[p]++,ds[q]++;
mx=max(mx,max(ds[p],ds[q]));
}
else a[++tt]=p,b[tt]=q,c[tt]=o;
}
deep[1]=1;
dfs(1,-1);
for(i=1; i<=tt; i++)
{
l=lca(a[i],b[i]);
if((deep[a[i]]+deep[b[i]]-2*deep[l])%2==0)
have[l].push_back(i);
ans+=c[i];
}
Dfs(1);
cout<<ans-dp[1][0];
}
