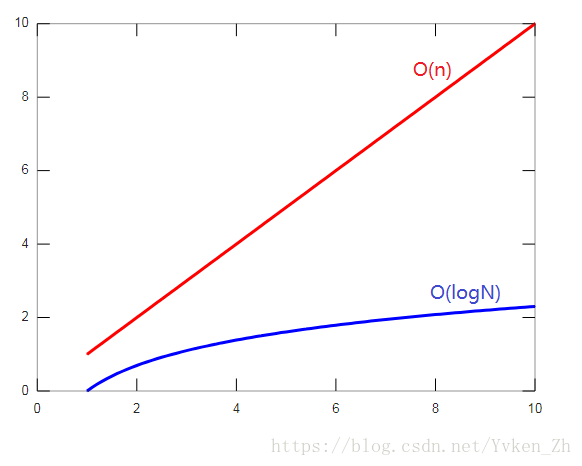
快速冪就是快速的求底數的整數次方，比起樸素的方法O(n)的時間複雜度，其時間複雜度是O(log2n)。這是很不錯的一個效率提升。

通常要求一個數X的Y次方，記做X^Y，樸素的計算方法是把X乘Y次得到這個結果。

而快速冪計算的過程是，對於指數Y進行奇偶性的判斷。為了方便解釋，記做：

ans = base ^exp

如果exp為奇數，那麼ans = ans * base;

如果exp為偶數，那麼ans = ans

然後每次base = base * base；並且每次迴圈指數減半，直到指數為0迴圈結束，ans就是所求結果。

例如求4^9

初始各成員的值分別為：ans = 1, base = 4,  exp = 9

1、第一次迴圈：指數exp=9為奇數，那麼

ans = ans * base = 4 

base = base * base = 4 ^ 2

指數減半，exp = 4

2、第二次迴圈：指數exp=4為偶數，那麼

ans = ans  = 4 

base = base * base = 4 ^ 4

指數減半，exp = 2

3、第三次迴圈：指數exp=2為偶數，那麼

ans = ans  = 4 

base = base * base = 4 ^ 8

指數減半，exp = 1

4、第四次迴圈：指數exp=1為奇數，那麼

ans = ans * base = 4^9 

base = base * base = 4 ^ 16

指數減半，exp = 0

迴圈結束，返回ans即所求結果。

可以看出，快速冪在求指數問題的時候，這裡只進行了4次的迴圈，Log2N加1向下取整，而普通的方法是迴圈9次進行乘法，當指數非常大的時候，這個差距是越來越大的，O(n)顯然是比不上O(log2N)。

快速冪在計算的時候， 指數是成半的減少，並且底數同時也是成倍增加，如果這樣：base^1，base^2,base^4,base^8,.....。從兩個方面同時計算冪次方。而樸素求冪則是底數線性的增加base^1,base^2,base^3,base^4,.....。底數的增加速度就遠不及快速冪，並且指數的減少也是逐一減少。

double Power(double base, int exponent) {
    if(exponent >= 0) {
		double ans = 1.0;
		while(exponent) {
			// 判斷是偶數還是奇數 和1進行與運算
			if(exponent & 1) {
				// 如果此時的指數 為1則為奇數 
				ans = ans * base;
			}
			base = base *base;         //底數進行乘方
			exponent = exponent >> 1;  //指數減半
		}
 
		return ans;
	}else {
		return 1.0 / Power(base, -1 * exponent); //指數為負數的情況 結果是一個分數
	}   
}