github部落格傳送門
csdn部落格傳送門

本章所需知識:

1. numpy

2. matplotlib

   資料下載連結:

3. 深度學習基礎網路模型(mnist手寫體識別資料集)

   梯度下降 BP 演算法手動實現

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(1, 100, 100)  # 造出一些100個偽資料 範圍在 1,100之間
y = 2 * x + np.random.randn(*x.shape) * 10  # 將x資料乘以2 再加上一些噪點

step = 0.00001  # 學習率 步長
diff = [0, 0]  # 梯度
cnt = 0  # 計數

b = 0  # b值初始化
w = 0  # w值初始化

error0 = 0  # 第一次誤差
error1 = 0  # 下一次誤差

epsilon = 0.000001  # 兩次誤差差值


def h(ax):
    return w * ax + b  # 定義一個主函式


while True:
    # cnt = cnt+1  # 計數 檢視訓練了多少次
    diff = [0, 0]
    for i in range(len(x)):  # 遍歷ax資料個數這麼多次
        diff[0] += h(x[i]) - y[i]  # 預測的y值 減去 原本的y的值 求和
        diff[1] += (h(x[i]) - y[i]) * x[i]  # 預測的y值 減去 原本的y值 乘以x的值 求和
    b = b - step / len(x) * diff[0]  # 更新b值 現在的 b 值 減去 學習率/x的個數*diff[0]的梯度
    w = w - step / len(x) * diff[1]  # 更新w值 現在的 w 值 減去 學習率/x的個數*diff[1]的梯度

    error1 = 0  # 重置本次擬合誤差為 0

    for i in range(len(x)):  # 計算本次 擬合誤差
        error1 += (y[i] - (b + w * x[i])) ** 2 / 2  # 均方差

    if abs(error1 - error0) < epsilon:  # 如果 本次擬合誤差 與 上次擬合誤差 小於設定閾值 則可跳出擬合迴圈
        break  # 跳出整個 擬合迴圈網路
    else:
        error0 = error1  # 否則將 本次誤差賦給 error0 以便下次迴圈擬合誤差相比較

    plt.ion()  # 開啟動態畫圖
    plt.clf()  # 清除畫板上的圖
    plt.plot(x, [h(x) for x in x])  # 畫出原本的x值 和 預測的y值 預測線
    plt.plot(x, y, 'bo')  # 再畫出 原本的x, y對應的點(樣本)
    print(w, b)  # 打印出當前訓練好的 w, b 的值
    plt.pause(0.1)  # 暫停 0.1 秒
    plt.ioff()  # 關閉所有畫板
 

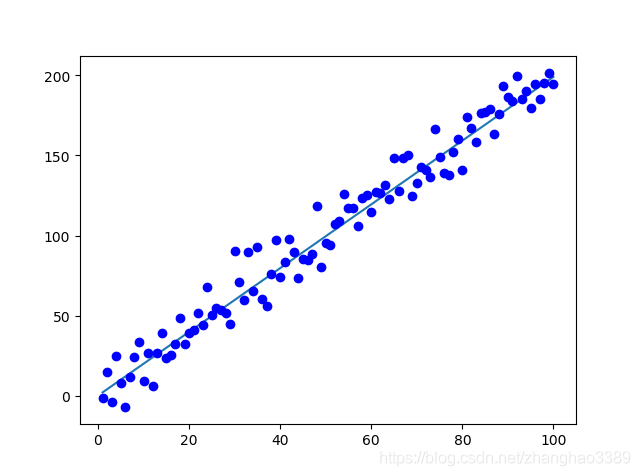
最後附上截圖訓練截圖: