kNN演算法

kNN演算法概述

kNN演算法和kmeans演算法的比較

knn工作原理:

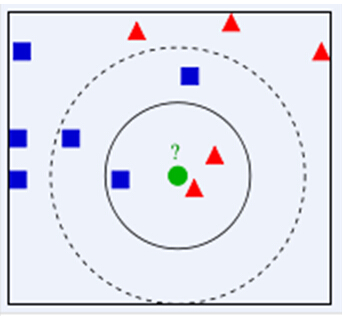
存在一個樣本資料集合(訓練樣本集),並且每個樣本都具有標籤,輸入新的樣本後,我們將樣本的特徵與訓練樣本集中的資料特徵比較,演算法提取特徵最相似的k個樣本的標籤,採用少數服從多數的形式,認為新樣本的標籤就是最相似的k個樣本中的主要標籤.

def classify0(inX,dataSet,labels,k):
    '''
    inX 待分類元素,是一個list
    dataset 訓練樣本集,是一個array物件
    labels 訓練樣本集標籤
    k kNN中的取前幾相近資料判斷
    '''
 

    dataSetSize = dataSet.shape[0]
    diffMat = tile(inX,(dataSetSize,1)) - dataSet
    # 下面三句其實就是做了個求待測資料到所有訓練樣本集資料的歐式距離
    sqdiffMat = diffMat**2
    sqDistances = sqdiffMat.sum(axis=1)
    distances = sqDistances**0.5
    # argsort是對distance進行排序(升序),返回的是元素的index 類似桶排序?
    sortedDistIndicies = distances.argsort()
    classCount = {}
    for
 
 i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse = True)
    # 第一次見到operator.itemgetter(i) 顧名思義返回的是一個方法(函式),用來獲取輸入引數的第i+1個值
    # 在sorted函式中給key賦值,使得key作為一個表示式,以item的第2個元素為索引排序
 

    # 3.x中用items返回一個list,元素是鍵值對構成的元組,同時keys返回一個所有鍵的list,value返回一個所有值的list
    return sortedClassCount[0][0]

def createSet():
    group = array([[1,1.1],[1,1],[0,0],[0,0.1]])
    labels = ['A','A','B','B']
    return group,labels

group,labels = createSet()
classify0([0,0.14],group,labels,3)

[('B', 2), ('A', 1)]


'B'

tile(item,dim)–tile函式用於將item按照dim複製成一個更大的向量,返回一個array
operator.itemgetter(i)– 顧名思義返回的是一個方法(函式),用來獲取輸入引數的第i+1個值

以上實現了一個簡單的knn分類器,完成了knn演算法的核心部分,但並不實用.
書中通過兩個例項,提高約會網站配對和?完整的演示機器學習演算法的流程

例1 實用knn演算法改進約會網站的配對效果

準備資料 從文字解析資料

資料是1000行約會網站的男性資訊,包括
- 每年獲得的飛行常客里程數
- 玩視訊遊戲所耗的時間百分比
- 每週消費的冰淇淋公升數

首先對資料進行處理和初步的觀察

def file2matrix(filename):
    fr = open(filename)
    arrayOLines = fr.readlines()
    numberOfLines = len(arrayOLines)
    returnMat = zeros((numberOfLines,3))
    classLableVector = []
    index = 0
    for line in arrayOLines:
        line = line.strip()
        listFromLine = line.split('\t')
        returnMat[index,:] = listFromLine[0:3]
        classLableVector.append(int(listFromLine[-1]))
        index += 1
    return returnMat,classLableVector

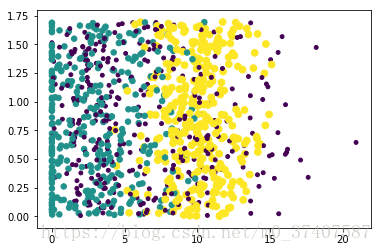
datingDataMat, datingLabels = file2matrix('/home/caid/mycode/MachineLearningInAction/MLIA_self/ch_02/datingTestSet2.txt')
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datingDataMat[:,1],datingDataMat[:,2],15.0*array(datingLabels),15.0*array(datingLabels))

<matplotlib.collections.PathCollection at 0x7f4001515898>

準備資料:歸一化資料

為了避免特徵之間,差值大的特徵對結果影響大,差值小的資料對結果影響小,需要對資料進行歸一化.歸一化的幾種方式,和標準化的區別.

歸一化的原理:

def autoNorm(DataSet):
    Maxval = DataSet.max(0)
    Minval = DataSet.min(0)
    ranges = Maxval - Minval
    NormDataSet = zeros(shape(DataSet))
    m = DataSet.shape[0]
    NormDataSet = DataSet - tile(Minval,(m,1))
    NormDataSet = NormDataSet/tile(ranges,(m,1))
    return NormDataSet,ranges,Minval

normMat,ranges,minVals = autoNorm(datingDataMat)
normMat
ranges
minVals

array([[ 0.44832535, 0.39805139, 0.56233353],
       [ 0.15873259, 0.34195467, 0.98724416],
       [ 0.28542943, 0.06892523, 0.47449629],
       ..., 
       [ 0.29115949, 0.50910294, 0.51079493],
       [ 0.52711097, 0.43665451, 0.4290048 ],
       [ 0.47940793, 0.3768091 , 0.78571804]])

array([ 9.12730000e+04, 2.09193490e+01, 1.69436100e+00])

array([ 0. , 0. , 0.001156])

def datingClassTest():
    hoRatio = 0.10
    datingDataMat,datingLabels = \
    file2matrix('/home/caid/mycode/MachineLearningInAction/MLIA_self/ch_02/datingTestSet2.txt')
    m = datingDataMat.shape[0]
    numTestVecs = int(m*hoRatio)
    NormDataMat,ranges,minvals = autoNorm(datingDataMat)
    errorCount = 0.0
    for i in range(numTestVecs):
        label = classify0(NormDataMat[i,:],\
                          NormDataMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
        # print("hte classifier came back with: %d, the real answer is %d" %(label,datingLabels[i]))
        if label != datingLabels[i]:errorCount += 1.0
    print("the total error rate is %.3f%%" %(errorCount/float(numTestVecs)*100.0))

datingClassTest()

the total error rate is 5.000%

通過測試演算法,可以看出這個分類器的結果的錯誤率在5%左右.為了使用演算法,需要提供一個介面

使用演算法:構建可用的系統

def classifyPerson():
    resultList = ['not at all','in small doses','in large doses']
    percentTats = float(input("percentage of time spent playing video game?"))
    ffMiles = float(input("ffmiles:"))
    iceCream = float(input("iceCream:"))
    datingDataMat,datingLabels = file2matrix('/home/caid/mycode/MachineLearningInAction/MLIA_self/ch_02/datingTestSet2.txt')
    normMat,ranges,minVals = autoNorm(datingDataMat)
    inArr = array([ffMiles,percentTats,iceCream])
    label = classify0((inArr-minVals)/ranges,datingDataMat,datingLabels,3)
    print("you will probably like this person:",\
         resultList[label-1])

classifyPerson()

percentage of time spent playing video game?10
ffmiles:10000
iceCream:0.5
you will probably like this person: in small doses

上例介紹瞭如何在資料中使用kNN分類器,下面這個例子將介紹如何在二進位制資料中利用kNN

例2 手寫識別系統

def img2vector(filename):
    returnVector = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVector[0,32*i+j] = int(lineStr[j])
    return returnVector

這是一個將測試資料轉換為資料集的一部分的函式,將一個32*32的方陣轉化為一個1*1024的行向量
接下來測試一下這個函式

testVector = img2vector('MLIA_self/ch_02/testDigits/0_13.txt')
testVector[0:32]

array([[ 0., 0., 0., ..., 0., 0., 0.]])

from os import listdir
def handWritingClassTest():
    hwLabels = []
    trainingFileList = listdir('MLIA_self/ch_02/trainingDigits')
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        filenameStr = trainingFileList[i]
        fileStr = filenameStr.split('.')[0]
        classLabel = int(fileStr.split('_')[0])
        hwLabels.append(classLabel)
        trainingMat[i,:] = img2vector('MLIA_self/ch_02/trainingDigits/%s' %filenameStr)

    testFileList = listdir('MLIA_self/ch_02/testDigits')
    n = len(testFileList)
    errorcount = 0.0
    for i in range(n):
        filenameStr = testFileList[i]
        fileStr = filenameStr.split('.')[0]
        classLabel = int(fileStr.split('_')[0])
        #hwLabels.append(classLabel)
        testImg = img2vector('MLIA_self/ch_02/trainingDigits/%s' %filenameStr)
        classifyResult = classify0(testImg,trainingMat,hwLabels,3) 
        # 第一次做計算還是沒有想清楚k是什麼,是最鄰近範圍,而不是測試集大小,也不是分成幾類
        if classifyResult != classLabel:
            errorcount += 1.0
    print("the number of error is : %f" % errorcount)
    print("the error rate is : %f " %(errorcount/float(n)))

handWritingClassTest()

the number of error is : 11.000000
the error rate is : 0.011628 

之所以kNN演算法能夠用在手寫數字識別上,並且能夠得到較好的結果,我認為從影象的角度看,同一個數字在影象中存在畫素的位置是相近的,如果兩個手寫數字的影象,有畫素的位置重合最多(即計算出來的距離最小)那麼它們就應該是同一個數字,對字母的識別相類似,另一方面,訓練集的數量足夠多,也是能夠達到較好效果的關鍵.

kNN演算法總結

kNN是分類資料最有效最簡單的演算法之一,但是使用演算法時,knn需要儲存全部資料集,並且對資料集中的每個資料計算距離,實際上需要大量的空間和時間開銷,另一個缺陷是無法給出任何資料的基礎結構資訊(什麼是基礎結構資訊?)因此,也無法知曉平均例項樣本和典型例項樣本具有什麼特徵.