題目描述

多米諾骨牌有上下2個方塊組成，每個方塊中有1~6個點。現有排成行的

上方塊中點數之和記為S1，下方塊中點數之和記為S2，它們的差為|S1-S2|。例如在圖8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每個多米諾骨牌可以旋轉180°，使得上下兩個方塊互換位置。 程式設計用最少的旋轉次數使多米諾骨牌上下2行點數之差達到最小。

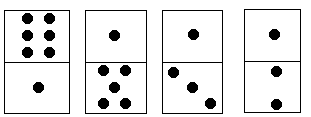
對於圖中的例子，只要將最後一個多米諾骨牌旋轉180°，可使上下2行點數之差為0。

輸入輸出格式

輸入格式：
輸入檔案的第一行是一個正整數n(1≤n≤1000)，表示多米諾骨牌數。接下來的n行表示n個多米諾骨牌的點數。每行有兩個用空格隔開的正整數，表示多米諾骨牌上下方塊中的點數a和b，且1≤a，b≤6。

輸出格式：
輸出檔案僅一行，包含一個整數。表示求得的最小旋轉次數。

輸入輸出樣例

輸入樣例#1： 複製
4
6 1
1 5
1 3
1 2
輸出樣例#1： 複製
1

這題就是一個揹包，揹包的本質就是對某一個元素的選取or不選。那麼對於這題也同樣適用，對於某一塊骨牌都有翻或者不翻兩種選擇。

我們設f[i][j]為前i塊骨牌上下差值為j時的最小翻轉次數，那麼狀態轉移就跟揹包差不多了。我們可以考慮對於j，必定是由前面的j+d或者j-d（d為上下差值）轉移過來的。那麼回到我們初始的說法，對於不翻，差值為j必定是由j-d轉移過來的，因為我們找到了第i塊，差值被強行加上來了，那麼當然是由j-d轉移了，翻轉了也同理，翻轉的時候記得把翻轉次數+1即可。最後找的時候ans<=1000就直接輸出即可，因為差值最小的時候遇到符合條件的就可以立刻輸出了。那為什麼是1000呢？因為我們最多翻轉1000次，n最大才1000，不存在翻超過1000次的可能，如果翻到了1001次，必定有重複的做法，不懂的話可以自己想想。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int f[1005][6010*3],a[1005],b[1005],cha,n,ans;
const int N=5000;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%d %d",&a[i],&b[i]);
	}
	memset(f,0x7f,sizeof(f));
	f[0][0+N]=0;
	for(int i=1;i<=n;i++)
	{
		int cha=a[i]-b[i];
		for(int j=-5000;j<=5000;j++)
		{
			f[i][j+N]=min(f[i-1][j-cha+N],f[i-1][j+cha+N]+1);
		}
	}
	for(int i=0;i<=5000;i++)
	{
		ans=min(f[n][N-i],f[n][N+i]);
		if(ans<=1000)
		{
			printf("%d",ans);
			return 0;
		}
	}
}