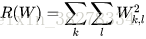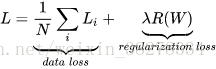損失函式 Loss function

在線性分類（上）筆記中，定義了從影象畫素值到所屬類別的評分函式（score function），該函式的引數是權重矩陣W。

在函式中，資料 $(x_i,y_{}$

回到上篇筆記貓影象分類例子中，它有針對“貓”，“狗”，“船”三個類別的分數。我們看到例子中權重值非常差，因為貓分類的得分非常低（-96.8），而狗（437.9）和船（61.95）比較高。我們將使用損失函式（Loss Function）（有時也叫代價函式Cost Function或目標函式Objective）來衡量我們對結果的不滿意程度。直觀地講，當評分函式輸出結果與真實結果之間差異越大，損失函式輸出越大，反之越小。

1. 多類支援向量機損失 Multiclass Support Vector Machine Loss

損失函式的具體形式多種多樣。首先，介紹常用的多類支援向量機（SVM）損失函式。

• SVM的損失函式想要SVM在正確分類上的得分始終比不正確分類上的得分高出一個邊界值 $\Delta$。

我們可以把損失函式想象成一個人，這位SVM先生（或者女士）對於結果有自己的品位，如果某個結果能使得損失值更低，那麼SVM就更加喜歡它。

讓我們更精確一些。回憶一下，第i個數據中包含影象 $x_i$的畫素和代表正確類別的標籤 $y_i$。評分函式輸入畫素資料，然後通過公式 $f(x_i,W)$來計算不同分類類別的分值。
這裡我們將分值簡寫為s。比如，針對第j個類別的得分就是第j個元素： $s_j=f(x_i,W)_j$。針對第i個數據的多類SVM的損失函式定義如下：

舉例：用一個例子演示公式是如何計算的。假設有3個分類，並且得到了分值s=[13,-7,11]。其中第一個類別是正確類別，即 $y_i=0$。同時假設 $\Delta$是10（後面會詳細介紹該超引數）。上面的公式是將所有不正確分類 $（j\not=y_i）$加起來，所以我們得到兩個部分：

可以看到第一個部分結果是0，這是因為[-7-13+10]得到的是負數，經過max(0,-)函式處理後得到0。這一對類別分數和標籤的損失值是0，這是因為正確分類的得分13與錯誤分類的得分-7的差為20，高於邊界值10。而SVM只關心差距至少要大於10，更大的差值還是算作損失值為0。第二個部分計算[11-13+10]得到8。雖然正確分類的得分比不正確分類的得分要高（13>11），但是比10的邊界值還是小了，分差只有2，這就是為什麼損失值等於8。

簡而言之，SVM的損失函式想要正確分類類別 $y_i$的分數比不正確類別分數高，而且至少要高 $\Delta$。如果不滿足這點，就開始計算損失值。

那麼在這次的模型中，我們面對的是線性評分函式( $f(x_i,W)=Wx_i$ )所以我們可以將損失函式的公式稍微改寫一下：

其中 $w_j$是權重W的第j行，被變形為列向量。然而，一旦開始考慮更復雜的評分函式 $f$公式，這樣做就不是必須的了。

在結束這一小節前，還必須提一下的屬於是關於0的閥值：max(0,-)函式，它常被稱為折葉損失（hinge loss）。

有時候會聽到人們使用平方折葉損失SVM（即L2-SVM），它使用的是 $max(0,-)^2$，將更強烈（平方地而不是線性地）地懲罰過界的邊界值。不使用平方是更標準的版本，但是在某些資料集中，平方折葉損失會工作得更好。可以通過交叉驗證來決定到底使用哪個。

2. 正則化

上面損失函式有一個問題。
假設有一個數據集和一個權重集W能夠正確地分類每個資料（即所有的邊界都滿足，對於所有的i都有 $L_i=0$）。問題在於這個W並不唯一：可能有很多相似的W都能正確地分類所有的資料。

一個簡單的例子：如果W能夠正確分類所有資料，即對於每個資料，損失值都是0。那麼當 $\lambda$>1時，任何數乘 $\lambda W$都能使得損失值為0，因為這個變化將所有分值的大小都均等地擴大了，所以它們之間的絕對差值也擴大了。舉個例子，如果一個正確分類的分值和距離它最近的錯誤分類的分值的差距是15，對W乘以2將使得差距變成30。

換句話說，我們希望能向某些特定的權重 $W$新增一些偏好，對其他權重則不新增，以此來消除模糊性,保證唯一性。這一點可以通過向損失函式增加一個正則化懲罰（regularization penalty）R(W)部分來實現的。

最常用的正則化懲罰是L2正規化，L2正規化通過對所有引數進行逐元素的平方懲罰來抑制大數值的權重：

上面的表示式中，將W中所有元素平方後求和。

注意正則化函式不是資料的函式，僅基於權重。

包含正則化懲罰後，就能夠給出完整的多類SVM損失函數了，它由兩個部分組成：資料損失（data loss），即所有樣例的的平均損失 $L_i$，以及正則化損失（regularization loss）。完整公式如下所示：

將其展開完整公式是：

其中，N是訓練集的資料量。現在正則化懲罰新增到了損失函式裡面，並用超引數 $\lambda$來計算其權重。該超引數無法簡單確定，需要通過交叉驗證來獲取。
除了上述理由外，引入正則化懲罰還帶來很多良好的性質，這些性質大多會在後續章節介紹。比如引入了L2懲罰後，SVM們就有了最大邊界（max margin）這一良好性質。

其中最好的性質就是對大數值權重進行懲罰，可以提升其泛化能力，因為這就意味著沒有哪個維度能夠獨自對於整體分值有過大的影響。

舉個例子

形象貼切易懂：
假設輸入向量x=[1,1,1,1]，兩個權重向量 $w_1=[1,0,0,0]$， $w_2=[0.25,0.25,0.25,0.25]$。那麼 $w^T_1x=w^T_2x=1$，兩個權重向量都得到同樣的內積，但是 $w_1$的L2懲罰是1.0，而 $w_2$的L2懲罰是0.25。因此，根據L2懲罰來看， $w_2$更好，因為它的正則化損失更小。從直觀上來看，這是因為 $w_2$的權重值更小且更分散。既然L2懲罰傾向於更小更分散的權重向量，這就會鼓勵分類器最終將所有維度上的特徵都用起來，而不是強烈依賴其中少數幾個維度。在後面的課程中可以看到，這一效果將會提升分類器的泛化能力，並避免過擬合。

需要注意的是，和權重不同，偏差沒有這樣的效果，因為它們並不控制輸入維度上的影響強度。因此通常只對權重W正則化，而不正則化偏差b。在實際操作中，可發現這一操作的影響可忽略不計。最後，因為正則化懲罰的存在，不可能在所有的例子中得到0的損失值，這是因為只有當W=0的特殊情況下，才能得到損失值為0。

3. 實際考慮(精髓)！！！

設定Delta
你可能注意到上面的內容對超引數 $\Delta$及其設定是一筆帶過，那麼它應該被設定成什麼值？需要通過交叉驗證來求得嗎？

現在看來，該超引數在絕大多數情況下設為 $\Delta=1.0$都是安全的。超引數 $\Delta$和 $\lambda$看起來是兩個不同的超引數，但實際上他們一起控制同一個權衡：即損失函式中的資料損失和正則化損失之間的權衡。
理解這一點的關鍵是要知道，權重W的大小對於分類分值有直接影響（當然對他們的差異也有直接影響）：當我們將W中值縮小，分類分值之間的差異也變小，反之亦然。 因此，不同分類分值之間的邊界的具體值（比如 $\Delta=1或\Delta=100$）從某些角度來看是沒意義的，因為權重自己就可以控制差異變大和縮小。也就是說，真正的權衡是我們允許權重能夠變大到何種程度（通過正則化強度 $\lambda$來控制）。

與二元支援向量機（Binary Support Vector Machine）的關係：在學習本課程前，你可能對於二元支援向量機有些經驗，它對於第i個數據的損失計算公式是：

其中，C是一個超引數，並且 $y_i\in\{-1,1\}$。可以認為本章節介紹的SVM公式包含了上述公式，上述公式是多類支援向量機公式只有兩個分類類別的特例。也就是說，如果我們要分類的類別只有兩個，那麼公式就化為二元SVM公式。這個公式中的C和多類SVM公式中的 $\lambda$都控制著同樣的權衡，而且它們之間的關係是 $C\propto\frac{1}{\lambda}$

備註：在初始形式中進行最優化。
如果在本課程之前學習過SVM，那麼對kernels，duals，SMO演算法等將有所耳聞。在本課程（主要是神經網路相關）中，損失函式的最優化的始終在非限制初始形式下進行。很多這些損失函式從技術上來說是不可微的（比如當x=y時，max(x,y)函式就不可微分），但是在實際操作中並不存在問題，因為通常可以使用次梯度。

備註：其他多類SVM公式。
需要指出的是，本課中展示的多類SVM只是多種SVM公式中的一種。

• 另一種常用的公式是One-Vs-All（OVA）SVM，它針對每個類和其他類訓練一個獨立的二元分類器。
• 還有另一種更少用的叫做All-Vs-All（AVA）策略。我們的公式是按照Weston and Watkins 1999 (pdf)版本，比OVA效能更強（在構建有一個多類資料集的情況下，這個版本可以在損失值上取到0，而OVA就不行。感興趣的話在論文中查閱細節）。
• 最後一個需要知道的公式是Structured SVM，它將正確分類的分類分值和非正確分類中的最高分值的邊界最大化。理解這些公式的差異超出了本課程的範圍。本課程筆記介紹的版本可以在實踐中安全使用，而被論證為最簡單的OVA策略在實踐中看起來也能工作的同樣出色（在 Rikin等人2004年的論文In Defense of One-Vs-All Classification (pdf)中可查）。

4. 無正則化損失函式的Python程式碼實現

有非向量化和半向量化兩個形式：

def L_i(x, y, W):
  """
  unvectorized version. Compute the multiclass svm loss for a single example (x,y)
  - x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
    with an appended bias dimension in the 3073-rd position (i.e. bias trick)
  - y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
  - W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
  """
  delta = 1.0 # see notes about delta later in this section
  scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
  correct_class_score = scores[y]
  D = W.shape[0] # number of classes, e.g. 10
  loss_i = 0.0
  for j in xrange(D): # iterate over all wrong classes
    if j == y:
      # skip for the true class to only loop over incorrect classes
      continue
    # accumulate loss for the i-th example
    loss_i += max(0, scores[j] - correct_class_score + delta)
  return loss_i

def L_i_vectorized(x, y, W):
  """
  A faster half-vectorized implementation. half-vectorized
  refers to the fact that for a single example the implementation contains
  no for loops, but there is still one loop over the examples (outside this function)
  """
  delta = 1.0
  scores = W.dot(x)
  # compute the margins for all classes in one vector operation
  margins = np.maximum(0, scores - scores[y] + delta)
  # on y-th position scores[y] - scores[y] canceled and gave delta. We want
  # to ignore the y-th position and only consider margin on max wrong class
  margins[y] = 0
  loss_i = np.sum(margins)
  return loss_i

def L(X, y, W):
  """
  fully-vectorized implementation :
  - X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
  - y is array of integers specifying correct class (e.g. 50,000-D array)
  - W are weights (e.g. 10 x 3073)
  """
  # evaluate loss over all examples in X without using any for loops
  # left as exercise to reader in the assignment

在本小節的學習中，一定要記得SVM損失採取了一種特殊的方法，使得能夠衡量對於訓練資料預測分類和實際分類標籤的一致性。還有，對訓練集中資料做出準確分類預測和讓損失值最小化這兩件事是等價的。

參考：https://zhuanlan.zhihu.com/p/20945670?refer=intelligentunit