機器學習演算法--聚類
常見的無監督學習型別:聚類任務 密度估計 異常檢測
聚類演算法試圖將樣本分成k個不想交的子集,每個子集稱為一個簇,對應一些潛在的概念。
樣本集x={x1, x2....xm} 每個樣本Xi={xi1,xi2...xin}對應n個特徵
劃分為K個不同的類別C={C1,C2....Ck} ,其中樣本xi的簇標記為i,則
={
1,
2,
m}可以表示聚類的結果。
1.效能指標:衡量聚類效果
資料集D={x1,x2..xm} 類別C={C1,C2..Ck} 簇標記向量 參考模型類別C*={C1*, C2*,....Cs*} 簇標記向量
定義:

Jaccard係數:
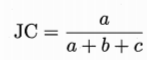
FM係數:

Rand係數:
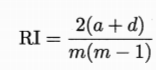
簇劃分C={C1,C2..Ck} 定義樣本距離dist(xi,xj)
樣本中心:![]()
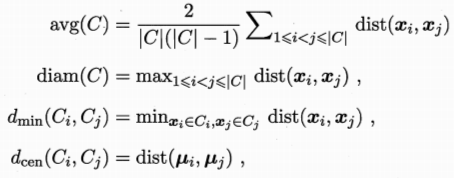
以上依次代表簇C中樣本間平均距離 樣本間最大距離 兩個簇的最小距離 兩個簇的中心距離
DB指數:

Dunn指數:
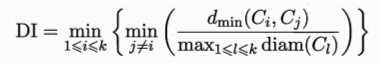
2.距離計算
樣本xi={xi1,xi2...xin} 樣本xj={xj1,xj2..xjn}
閔可夫斯基距離:

p=2歐式距離:
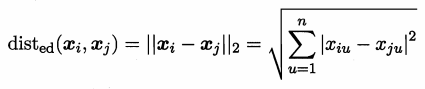
p=1曼哈頓距離:

離散屬性等無序屬性不能直接計算距離,可採用VDM方式來計算:
mua表示屬性u上取值為a的樣本數 muai表示在第i個簇中取值為a的樣本數 k為總簇數
在屬性u上離散值a,b的距離:

當n個屬性有nc個有序,後面無序時有:

當不同屬性值權重不同時:
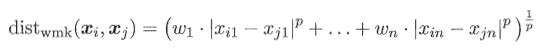
原型聚類
原型:樣本空間中具有代表的點
原型聚類:基於原型的聚類演算法 K-means均值演算法 學習向量量化 高斯混合聚類 密度聚類 層次聚類
1.K-means均值演算法
樣本集D={(x1,y1),(x2,y2)...(xm,ym)} 簇Ci的均值向量ui
![]()
最小化平方誤差:
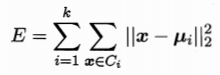
刻畫了簇內樣本圍繞均值向量的緊密程度

給定樣本集,從中隨機挑選k個樣本作為初始均值向量,然後計算各個樣本到各個均值向量的距離,對於每個樣本,劃分到距離均值最近的類中去。劃分完畢後,重新計算k個類的均值向量,再次執行劃分過程。終止條件:最大迭代係數 最小調整幅度 或者均值向量不再更新。
2.學習向量量化LVQ
資料集D={(x1,y1),(x2,y2)...(xm,ym)} xj=(xj1,xj2...xjn) 類別標記yj={Y} LVQ學得一組原型向量{p1, p2..pq}分別代表q個簇。

初始化q個原型向量,分別預設類別標記{t1, t2...tq} 隨機選擇一個樣本計算該樣本到各個原型向量的距離,求出最近的原型向量。比較最近原型向量與樣本的類別標記
假設更新完之後的原型向量為p`,其與xj的距離為:

即當0<<1時,新原型向量與樣本的距離會減小。
若相同,則原型向量更為:
![]()
若不同,則原型向量更新為:
![]()
繼續選擇新樣本,進行迭代計算
終止條件:最大迭代次數 原型向量不在更新或者更新很小
獲得原型向量之後,樣本xi可以劃分到距離樣本最近的原型向量代表的簇中

3.高斯混合聚類
多元高斯分佈:
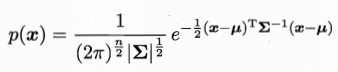
x為n維樣本 u為均值向量 方差矩陣
高斯混合分佈:

假設樣本的生成過程由高斯分佈給出:隨機變數zj={1,2....k} 表示生成樣本xj的高斯混合成分 zj的先驗概率對應於ai
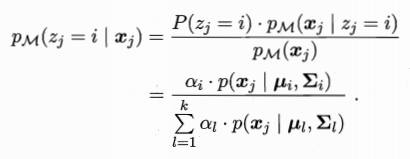
樣本xj由第i個高斯混合成分組成的概率pm(zj = i | xj) 記為yji
高斯混合聚類把樣本集分為k個簇 C={C1,C2...Ck} 每個簇的標記
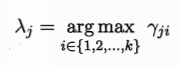
最大化對數似然:

高斯混合模型的EM演算法:
E:根據模型引數計算每個樣本屬於每個高斯成分的後驗概率yji
M:根據後驗概率來更新模型引數,使最大化對數似然
最大化對數似然,及最大化ui以及i
對於ui求導:
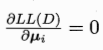

![]()

對於i求導:
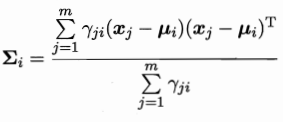
考慮約束:

拉格朗日乘子法:
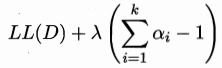
對於ai求導等於0:
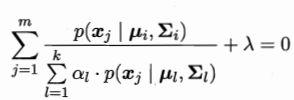
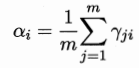
演算法流程:

4.密度聚類
給定資料集D={(x1,y1),(x2,y2)...(xm,ym)} 定義:
鄰域:
![]()
核心物件:
![]()
密度直達:xi是核心物件 xj位於xi的鄰域內,則稱xj與xi密度直達
密度可達:對於xi與xj 存在序列p1,p2,,pn p1=xi,pn=xj pi+1由pi密度直達,則xi與xj密度可達
密度相連:存在xk,使得xi,xj均與xk密度相連,則稱xi與xj密度相連
簇:由密度可達關係匯出的最大密度相連樣本集合

5.層次聚類
AGNES自低向上層次聚類:初始每一個樣本看成一個簇,然後合併距離最近的兩個簇,直到簇總數滿足預定條件。
簇距離計算: