機器學習-*-DBSCAN聚類及程式碼實現
DBSCAN
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪聲的基於密度的聚類方法)
原理
首先描述以下幾個概念,假設我們有資料集
,則
1.
鄰域:對於
,有
,該鄰域的資料個數為
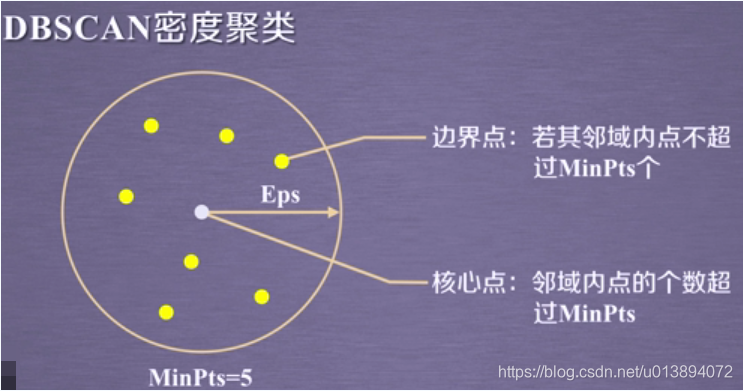
2.核心點:設最小鄰域內個數為
,若一點
的
鄰域的
,則稱該點為核心點
3.邊界點:若一點
的
鄰域內
,且處於核心點鄰域內的點,則稱該點為邊界點
4.噪聲點:不是核心點和邊界點的其他點為噪聲點。
5.密度直達:如果
在核心點
的鄰域內,則它倆就是密度直達的
6.密度可達:若有核心物件序列
,若
均可以由
密度直達,則稱
與
密度可達
密度直達和密度可達是不對稱的,不能絕對的反向匯出,參見參考文獻1
7.密度相連:有點
,若他們與核心物件
密度可達,那麼他們倆是密度相連的。這個概念可以對稱的。
下邊是網上擷取的相關示例
聚類流程
首先闡述一下聚類的思想:以某一核心點為基點,根據密度可達關係、密度相連關係,匯出最大樣本集類簇,此為第一個類簇;再從剩下的核心點中選取新的為基點重複上述過程;直到所有的核心點被選取完畢,若剩下了樣本點,每一個樣本點均為一個類別。
具體流程:
1.初始化核心點集合
,遍歷資料找到所有的核心點,建立類簇集合
2.若
停止迭代 轉6,否則
中隨機選取一個核心點
(不放回),轉3
3.以當前核心點為原點建立一個新的類簇
,建立當前子樣本集
,子核心點集
,將核心點加入
和
4.遍歷
,拿取一個核心點(不放回),查詢其相關鄰域內的點
,
中的點加入
,將
與原始核心點集
做交集,得到的集合再與
做並集。
5.不斷重複3-4,直到
為空,將
中的點作為類簇
的成員,
加入
,轉2
6.查詢餘下的未加入到
