1.（連通網的）最小生成樹問題提出：假設要在n個城市之間建立通訊聯絡網，則連通n個城市只需要修建n-1條線路，如果在最節省經費的前提下建立這個通訊網？該問題等價於：構造網的一棵最小生成樹，即：在e條帶權的邊中選取n-1條邊（不構成迴路），使權值之和為最小。有兩種演算法：Prim（普利姆）演算法和Kruskal（克魯斯卡爾）演算法。

2.Prim演算法的基本思想（加點法）：取圖中任意一個頂點v作為生成樹的根，之後往生成樹上新增新的頂點w。在新增的頂點w和已經在生成樹上的頂點v之間必定存在一條邊，並且該邊的權值在所有連通頂點v和w之間的邊中取值最小。之後繼續往生成樹上新增頂點，直至生成樹上含有n個頂點為止。一般情況下所新增的頂點應滿足下列條件：在生成樹的構造過程中，圖中n個頂點分屬兩個集合：已落在生成樹上的頂點集U和尚未落在生成樹上的頂點集V-U，則應在所有連通U中頂點和V-U中頂點的邊中選取權值最小的邊。例如下圖最小生成樹的生成過程：

3.Kruskal演算法的基本思想（加邊法）：

（1）考慮問題的出發點：為使生成樹上邊的權值之和達到最小，則應使生成樹中每一條邊的權值儘可能小。

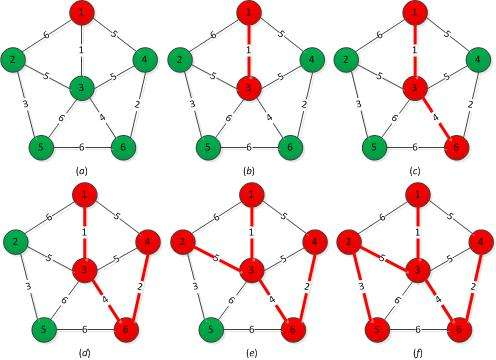
（2）具體做法：先構造一個只含n個頂點的子圖SG，然後從權值最小的邊開始，若它的新增不使SG中產生迴路，則在SG上加上這條邊，直至加上n-1條邊為止。例如下圖最小生成樹的生成過程：

演算法描述：

構造非連通圖ST = (V, {});

k = i = 0; //k計選中的邊數

while (k < n - 1)

{

　　i++;

　　檢查邊集E中第i條權值最小的邊(u, v); 若(u, v)加入ST後不使ST中產生迴路，則輸出邊(u, v); 且k++;

}

5.兩種演算法適用範圍：普利姆演算法適用於稠密圖，克魯斯卡爾演算法適用於稀疏圖。