競賽圖(tournament)學習筆記

現在只是知道幾個簡單的性質。。。

競賽圖也叫有向完全圖。

其實就是無向完全圖的邊有了方向。

​ 有一個很有趣的性質就是:一個tournament要麼沒有環，如果有環，那麼必然有一個三元環。當然，tournament一定沒有自環和二元環。

​ 證明的話，開始吧，，

​ 首先我們假定當前的tournament存在一個N元環，那麼我們設A,B,C為這個N元環上連續的三個點，那麼就會存在AB和BC兩條邊，又因為是競賽圖，所以一定會存在AC或者CA兩者中的一條邊。

​ 又可以開始開心地分情況討論了：

​ (一)，存在CA邊，那麼很開心，我們已經找到了三元環ABC。

​ (二)，存在AC邊，那麼我們就會發現B這個點是沒有用的了，比如這樣：

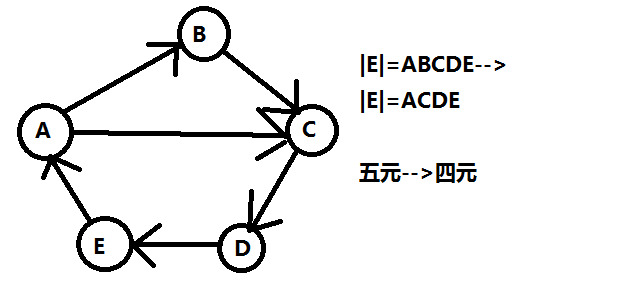
那麼我們就可以把一個N元環變成N-1元環了。

那麼就一定會縮小到3元環了。

上述性質例題：

CF117C Cycle

一個tournament是一個沒有自環的有向圖，同時，每兩個點之間有一條邊連線。這就是說，對於兩個點u，v（u≠v），有一條從u到v的邊或一條從v到u的邊。

給你一個tournament，請找出一個長度為3的環。

直接按照上述性質模擬就好了。

code：

#include <iostream>
#include <cstdio>

using namespace std;

const int wx=5017;

inline int read(){
    int sum=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
    while(ch>='0'&&ch<='9'){sum=(sum<<1)+(sum<<3)+ch-'0'; ch=getchar();}
    return sum*f;
}

char s[wx][wx];
int vis[wx];
int n;

bool dfs(int u,int fa){
    vis[u]=1;
    for(int i=1;i<=n;i++){
        if(s[u][i]-'0'){
            if(s[i][fa]-'0'){
                printf("%d %d %d\n",fa,u,i);
                return true;
            }
            if(!vis[i])if(dfs(i,u))return true;
        }
    }
    return false;
}

int main(){
    n=read();
    for(int i=1;i<=n;i++)
        scanf("%s",s[i]+1);
    int fl=0;
    for(int i=1;i<=n;i++)
        if(!vis[i])
            if(dfs(i,i))return 0;;
    puts("-1");
    return 0;
}
 

關於其他性質：

1：任意競賽圖都有哈密頓路徑（經過每個點一次的路徑，不要求回到出發點）。

2：競賽圖存在哈密頓迴路的充要條件是強聯通。

先留坑。