鄰接矩陣建圖

定義

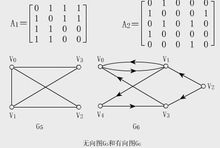
分為V（點）和E（邊）集合。因此，用一個一維陣列存放圖中所有頂點資料；用一個二維陣列存放頂點間關係（邊或弧）的資料，這個二維陣列稱為鄰接矩陣。鄰接矩陣又分為有向圖鄰接矩陣和無向圖鄰接矩陣。

鄰接矩陣（Adjacency Matrix）是表示頂點之間相鄰關係的矩陣。設G=(V,E)是一個圖，其中V={v1,v2,…,vn} [1] 。G的鄰接矩陣是一個具有下列性質的n階方陣：
①對無向圖而言，鄰接矩陣一定是對稱的，而且主對角線一定為零（在此僅討論無向簡單圖），副對角線不一定為0，有向圖則不一定如此。
②在無向圖中，任一頂點i的度為第i列（或第i行）所有非零元素的個數，在有向圖中頂點i的出度為第i行所有非零元素的個數，而入度為第i列所有非零元素的個數。
③用鄰接矩陣法表示圖共需要n^2個空間，由於無向圖的鄰接矩陣一定具有對稱關係，所以扣除對角線為零外，僅需要儲存上三角形或下三角形的資料即可，因此僅需要n（n-1）/2個空間。

程式碼實現

1、直接給出鄰接矩陣

輸入檔案如下

5
0 2 2 3 0
2 0 1 0 3
2 1 0 0 2
3 0 0 0 4
0 3 2 4 0

scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
	for(int j = 1; j <= n; ++j) {
		scanf("%d", &a[i][j]);
	}
}

2、給出邊的頂點

輸入：兩個邊的頂點和權值

5 7
1 2 2
1 3 2
1 4 3
2 3 1
2 5 3
3 5 2
4 5 4

scanf("%d %d", &m, &n);
for(int i = 1; i <= n; ++i) {
	for(int j = 1; j <= n; ++j) {
		int x, y, z;
		scanf("%d %d %d", &x, &y, &z);
		a[x][y] = z;
		a[y][x] = z;//無向圖 
	}
}
 

鄰接表建圖

//其實我也不是很懂
struct Edge {
  int next;
  int to;
  int dis;
}edge[maxm]; //結構體表示靜態鄰接表
//建圖
int num_edge = 0;
void addedge(int from, int to, int dis)  { 
  edge[++num_edge].next = head[from]; //鏈式儲存下一條出邊
  edge[num_edge].to = to; //當前節點編號
  edge[num_edge].dis = dis; //本條邊的距離
  head[from] = num_edge; //記錄下一次的出邊情況
}