吳恩達改善深層神經網路引數:超引數除錯、正則化以及優化——優化演算法
阿新 • • 發佈:2018-11-26
機器學習的應用是一個高度依賴經驗的過程,伴隨著大量的迭代過程,你需要訓練大量的模型才能找到合適的那個,優化演算法能夠幫助你快速訓練模型。
難點:機器學習沒有在大資料發揮最大的作用,我們可以利用巨大的資料集來訓練網路,但是在大資料下訓練網路速度很慢;
使用快速的優化演算法大大提高效率
mini-batch梯度下降法
向量化能讓你有效的對所有的m個例子進行計算,允許你處理整個訓練集而無需某個明確的公式。
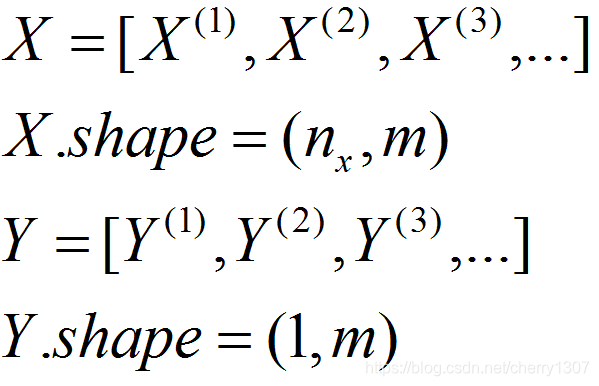
m很大時,處理速度非常慢 在對整個訓練集進行梯度下降時,必須處理整個訓練集,才能進行下一步梯度下降。 假設有500萬個資料,必須處理完500萬個資料,才能進行下一步梯度下降。
mini—beach
將訓練集分成小一點的子集
將500萬個資料沒1000個分為一組,分為5000個子集
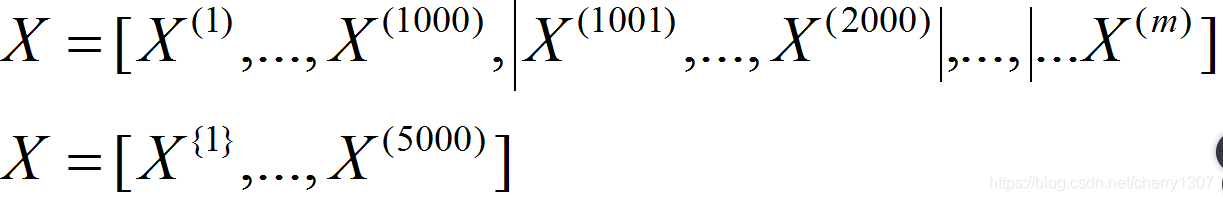
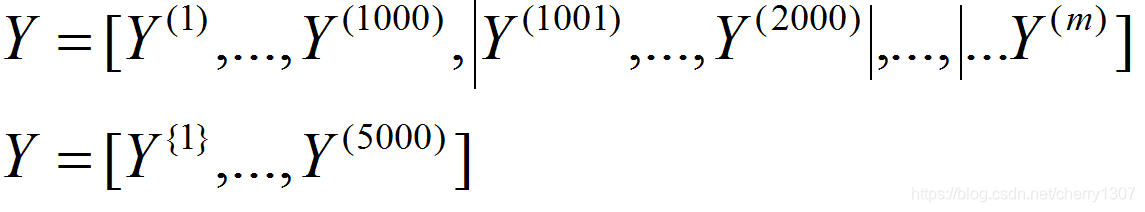
mini—beach的資料集就變成了X^{t},Y^{t}
X^{1}Y^{1}中有1000個樣本
同時處理單個mini-batchX^{t},Y^{t}
#演算法 { for t = 1,...,5000{ #forward propagation on X^{t} #向量化處理1000個樣本 Z^[l] = W^[l]*A^[l-1]+b^[l] A^[l] = g^[l](Z^[l]) #cost function cost = 1/1000*sum(L(yhat{t}-y{t}))+lamabd/(2*1000)*sum||w^[t]||^2 `#backward propagation dAL = dL(AL,Y)/dAL dZ^[l]=g'^[l]*dAL dW^[l]=dZ^[l]*A^[l-1]T db^[l]=dZ^[l] dA_prev = dZ^[l]T*W^[l] #mini-batch W^[l]=W^[l]-alpha*dW^[l] b^[l]=b^[l]-alpha*db^[l] } }
梯度下降:一次遍歷訓練集,只能讓你做一個梯度下降
mini-batch:一次遍歷訓練集,做5000個梯度下降
多次遍歷訓練集,最外層還需要一個while/for循壞,使能收斂到一個合適的精度。
理解mini-batch剃度下降法
梯度下降法
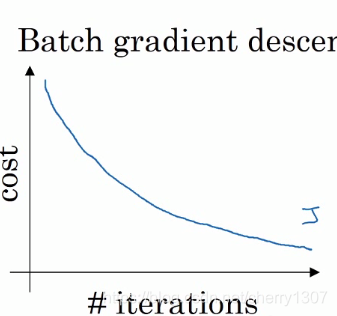
mini-batch梯度下降法
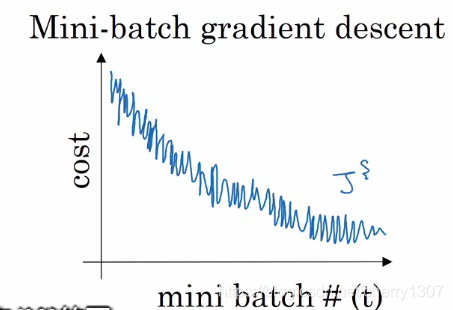
趨勢向下
mini-batch的size
if mini-batch size = m --> 梯度下降法 相對噪音低,幅度大,單次迭代耗時長 if mini-batch size = 1 -->隨機梯度下降法 噪音大,最終靠近最小值有時偏離,因為它永不收斂 失去向量化帶來的加速 mini-batch size 介於1,m之間
怎樣尋選擇m?
if small train set:(<2000)
梯度下降
typical mini-batch size:
64(2^6) 128(2^7),256(2^8),512(2^9)
x^{t},Y^{t}符合CPU、GPU記憶體
指數加權平均
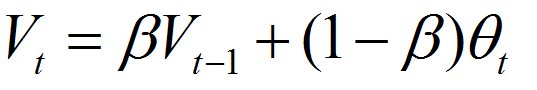
V^theta = 0
repeat{
get next theta^t
V^theta := bata*V^theta + (1-bata)*theta^t
}
指數加權平均的偏差
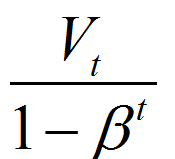
動量梯度下降法
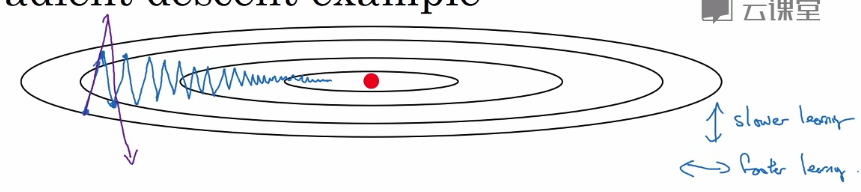
在縱軸上,希望學習慢一點
在橫軸上,希望學習快一點
動量梯度下降法:
V_dW= 0
V_db = 0
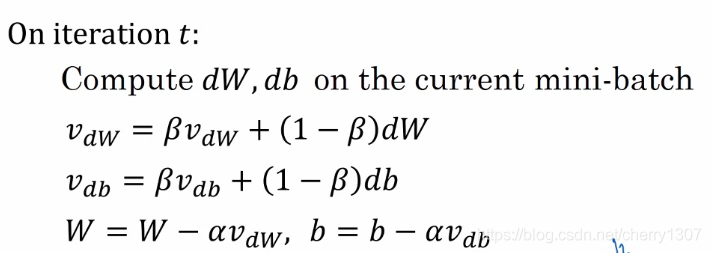
超引數:alpha,bata
bata一般取0.9
RMSprop
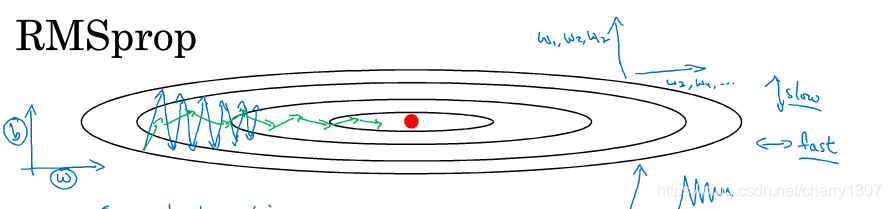
消除擺動
允許使用更大的學習率
On iteration t:
compute dW,db on current mini-batch
S_dw = bata_2*S_dW + (1-bata_2)*(dW)^2
S_db = bata_2*S_db + (1-bata_2)*(db)^2
W := W - alpha*dW/(sqrt(S_dW)+e)
b:= b - alpha*db/(sqrt(S_db)+e)
adam優化器
S_dW =0,S_db = 0,V_dW =0,V_db = 0
On iteration t:
compute dW,db on current mini-batch
V_dW = bata_1*V_dW + (1-bata_1)*(dW)^2
V_db = bata_1*V_db + (1-bata_1)*(db)^2
S_dW = bata_2*S_dW + (1-bata_2)*(dW)^2
S_db = bata_2*S_db + (1-bata_2)*(db)^2
V^vorrect_dW = V_dW/(1-bata_1^t) V^vorrect_db = V_db/(1-bata_1^t)
S^vorrect_dW = S_dW/(1-bata_2^t) S^vorrect_db = S_db/(1-bata_2^t)
W := W - alpha*V^vorrect_dW/(sqrt(S^vorrect_dW)+e)
b := b - alpha*V^vorrect_db/(sqrt(S^vorrect_db)+e)
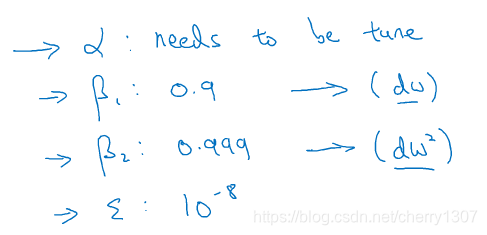
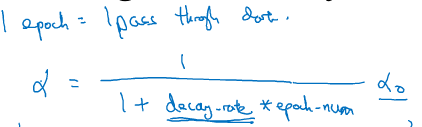
學習率衰減
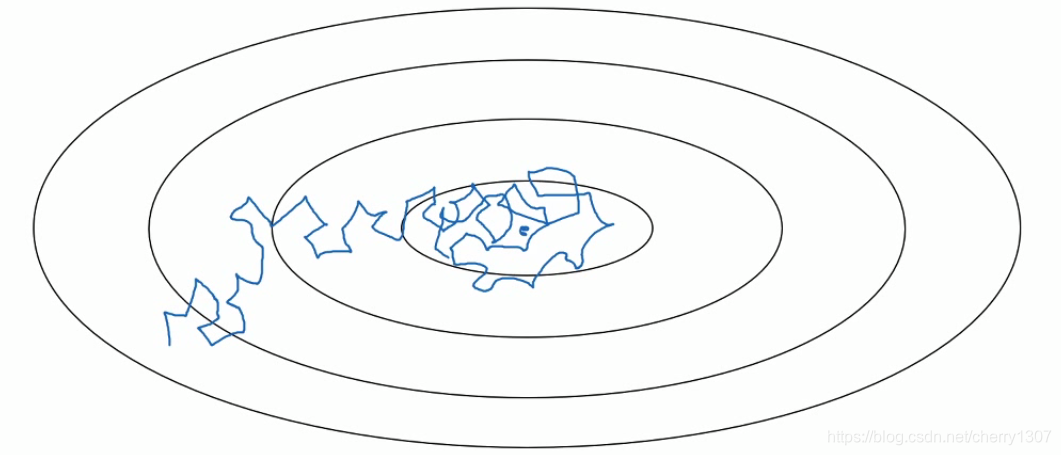
有時候使用固定學習率,在不會收斂
使用衰減的學習率,在學習初期,能承受較大的步伐,但當開始收斂的時候,小的學習率會讓步伐變小