1. 剩餘系

指模正整數n的餘數所組成的集合。
若一個剩餘系中包含了這個正整數n所有可能的餘數，則稱為完全剩餘系，記為Zn。（一般地，對於任意正整數n，有n個餘數：0,1,2,…,n-1）
簡化剩餘系：簡化剩餘系也稱既約剩餘系或縮系，是m的完全剩餘系中與m互素的數構成的子集。

2. 定義

若Zn中的兩元素滿足a*b=1，則稱a，b互為模n意義下的乘法逆元。

3.實現

3.1 單個查詢

3.1.1 擴歐

#include<bits/stdc++.h>
#define mo 100003
using namespace std;
int a,b,x,y,n,
 
p;
int exgcd(int a,int b,int &x,int &y){
    if(b==0){
        x=1;y=0;
        return a;
    }
    else{
        int ret=exgcd(b,a%b,y,x);
        y-=x*(a/b);
        return ret;
    }
}
int main(){
    scanf("%d%d",&n,&p);
    int tx=exgcd(n,p,x,y);
        tx=x;
        while(tx<0)
 
 tx+=p;
        while(tx>=p) tx-=p;
        cout<<tx<<endl;
    return 0;
}

3.1.2 快速冪

#include<bits/stdc++.h>
using namespace std;
int x,y,n,mo;
long long fpow(long long x,long long w){
    long long ans=1,res=w;
    while(x){
        if(x&1) ans*=res,ans%=mo;
        res*
 
=res,res%=mo;
        x/=2;
    }
    return ans;
}
int main(){
    scanf("%d%d",&n,&mo);
        long long tx=fpow(mo-2,n);
        cout<<tx<<endl;
    return 0;
}

3.1.3 擴歐與快速冪的比較

據說是擴歐略快。

3.2 線性求法

3.2.1 遞推法

#include<bits/stdc++.h>
using namespace std;
int a[3000010],n,p;
int main(){
    scanf("%d%d",&n,&p);
    a[1]=1;
    printf("%d\n",a[1]);
    for(register int i=2;i<=n;i++){
        a[i]=1ll*(p-p/i)*a[p%i]%p;
        printf("%d\n",a[i]);
    }
    return 0;	
}

3.2.2倒推法

先求n！的逆元，然後倒推求出1！……（n-1）!的逆元（見3.3），然後根據（如圖）即可推出。

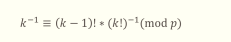
3.3 階乘的逆元

	for(int i=1;i<=n;i++) fac[i]=i*fac[i-1]%mo;//階乘
	inv[n]=f_mul(fac[n],mo-2);//n!的逆元
	for(int i=n-1;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mo;//倒推