文章目錄

• 1. 概率論
• 1.1 條件概率
• 1.2 全概率公式
• 1.3 貝葉斯公式
• 1.4 獨立性
• 2. 簡單圖分析（簡單貝葉斯網路獨立性分析）
• 3. 樸素貝葉斯
• 3.1樸素貝葉斯的推導
• 3.2 高斯樸素貝葉斯（Gaussian Naive Bayes）
• 3.3 多項分佈樸素貝葉斯（Multinomial Native Bayes）

1. 概率論

與之相關的有概率論的一些知識，這裡先做簡單知識複習。

1.1 條件概率

條件概率是指事件A在另外一個事件B已經發生條件下的發生概率。條件概率表示為：P（A|B），讀作“在B的條件下A的概率”。若只有兩個事件A，B，那麼 $P\left(A\mathrm{\mid }B\right)$

1.2 全概率公式

定義：（完備事件組/樣本空間的劃分）
設B1，B2，…Bn是一組事件,若
（1） $\forall_i \neq j \epsilon \{1,2,...n\},B_inB_j= \emptyset$
（2）B1∪B2∪…∪Bn=Ω
則稱B1，B2，…Bn樣本空間Ω的一個劃分，或稱為樣本空間Ω 的一個完備事件組。
定理（全概率公式）：
設事件組 $\{B\}$是樣本空間Ω 的一個劃分，且P（Bi）>0（i=1，2，…n）則對任一事件B，有 $P(A)=\sum_{i=1}^nP(B_i)P(A|B_i)$

1.3 貝葉斯公式

設B1，B2，…Bn…是一完備事件組，則對任一事件A，P（A）>0，有 $P(B_i|A)=\frac {P(AB_i)}{P(A)}=\frac {P(B_i)P(A|B_i)}{\sum_i P(B_i)P(A|B_i)}$

1.4 獨立性

當且僅當兩個隨機事件A與B滿足P(A∩B)=P(A)P(B)的時候，它們才是統計獨立的，這樣聯合概率可以表示為各自概率的簡單乘積。同樣，對於兩個獨立事件A與B有P(A|B)=P(A)以及P(B|A)=P(B)換句話說，如果A與B是相互獨立的，那麼A在B這個前提下的條件概率就是A自身的概率；同樣，B在A的前提下的條件概率就是B自身的概率。

2. 簡單圖分析（簡單貝葉斯網路獨立性分析）

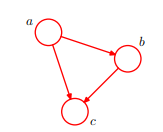
$P(A,B,C)=P(C|A,B)P(B|A)P(A)$ 這個是對上面圖的簡單表示三個變數a，b，c的聯合概率分佈。對這個簡單圖有一定了解後深入瞭解會的到下列幾個有趣的結論，後面可能會用到。

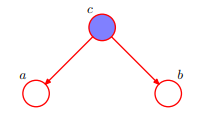
即 ：在c給定的條件下，a，b被阻斷（blocked）是獨立的。

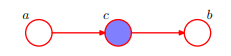
即 ：在c給定的條件下，a，b被阻斷（blocked）是獨立的。

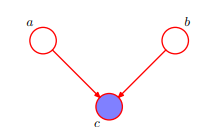
即 ：而對於上圖，在c未知的條件下，a，b被阻斷（blocked）是獨立的。
上面都是可以根據基本公式推匯出來，如果感興趣可以參考 ： PRML 模式識別與機器學習

3. 樸素貝葉斯

樸素貝葉斯（Naive Bayes，NB）是基於** “特徵之間是獨立的”**這一樸素假設，應用貝葉斯定理的監督學習演算法。

3.1樸素貝葉斯的推導

• 對於給定的特徵向量 $x_1,x_2,...,x_n$
• 類別 y 的概率可以依據貝葉斯公式得到： $P(y|x_1,x_2,...,x_n)=\frac{P(y)P(x_1,x_2,...,x_n|y)}{P(x_1,x_2,...,x_n)}$