最近在進行相機標定和相機成像範圍計算時，需要用到相機座標轉換關係中的影象座標到世界座標的轉換，檢索到這篇博文【四個座標系之間的變換關係】，覺得講解簡練清晰易懂，故進行轉載分享如下，供更多人學習。

轉自：https://blog.csdn.net/lyl771857509/article/details/79633412

 

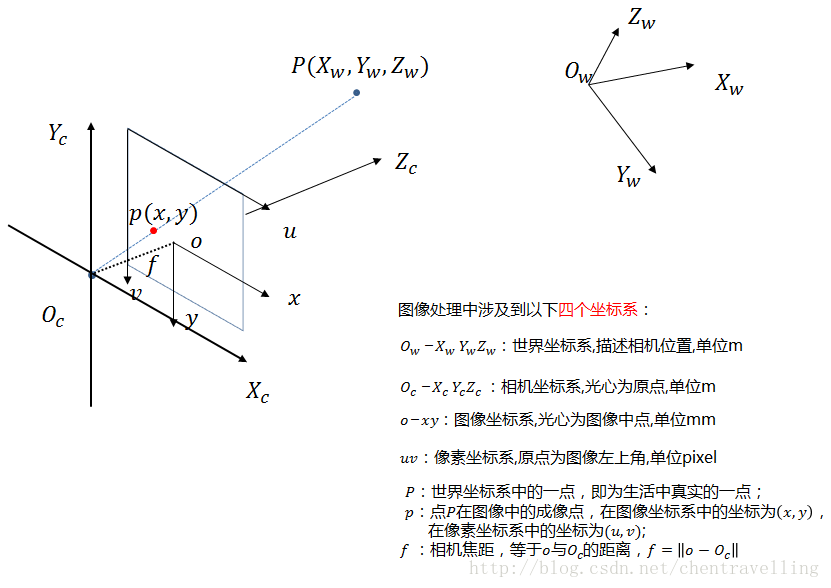
世界座標系，相機座標系，影象物理座標系，畫素座標系之間的關係：

1：世界座標系：根據情況而定，可以表示任何物體，此時是由於相機而引入的。單位m。
2：相機座標系：以攝像機光心為原點（在針孔模型中也就是針孔為關心），z軸與光軸重合也就是z軸指向相機的前方（也就是與成像平面垂直），x軸與y軸的正方向與物體座標系平行，其中上圖中的f為攝像機的焦距。單位m
3：影象物理座標系

（也叫平面座標系）：用物理單位表示畫素的位置，座標原點為攝像機光軸與影象物理座標系的交點位置。座標系為圖上o-xy。單位是mm。單位毫米的原因是此時由於相機內部的CCD感測器是很小的，比如8mm x 6mm。但是最後影象照片是也畫素為單位比如640x480.這就涉及到了影象物理座標系與畫素座標系的變換了。下面的畫素座標系將會講到。
4：畫素座標系：以畫素為單位，座標原點在左上角。這也是一些opencv，OpenGL等庫的座標原點選在左上角的原因。當然明顯看出CCD感測器以mm單位到畫素中間有轉換的。舉個例子，CCD感測上上面的8mm x 6mm，轉換到畫素大小是640x480. 假如dx表示畫素座標系中每個畫素的物理大小就是1/80. 也就是說毫米與畫素點的之間關係是piexl/mm.
好了四個座標系都解釋完了，接下來就說下各個座標系中間的變換關係吧。

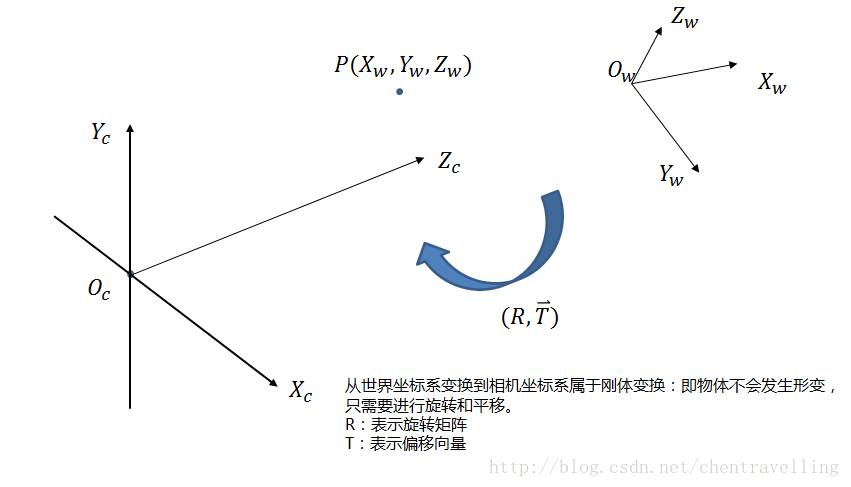
一、世界座標到相機座標系

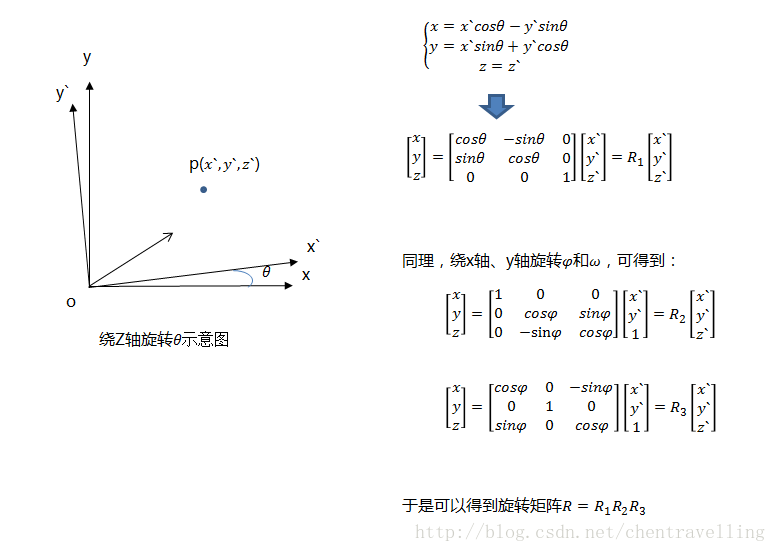
物體之間的座標系變換都可以表示座標系的旋轉變換加上平移變換，則世界座標系到相機座標系的轉換關係也是如此。繞著不同的軸旋轉不同的角度得到不同的旋轉矩陣。如下：

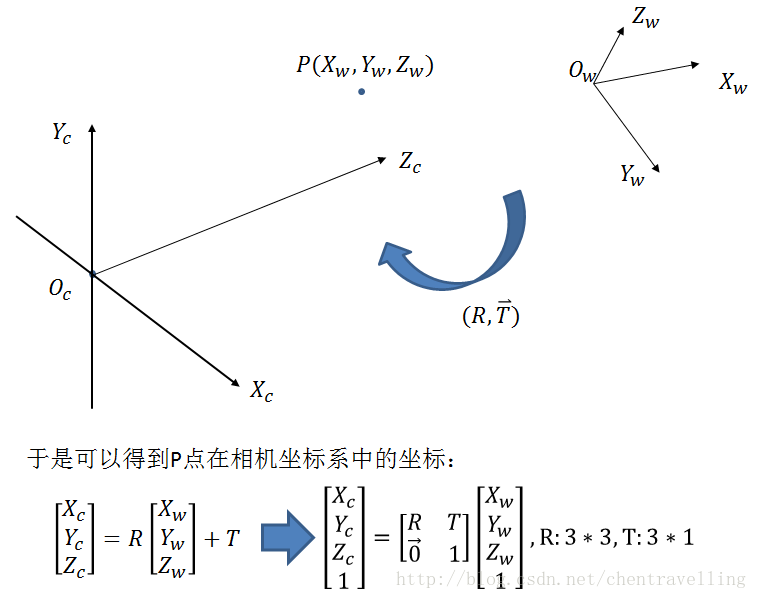
那麼世界座標系到相機座標系的變換如下：

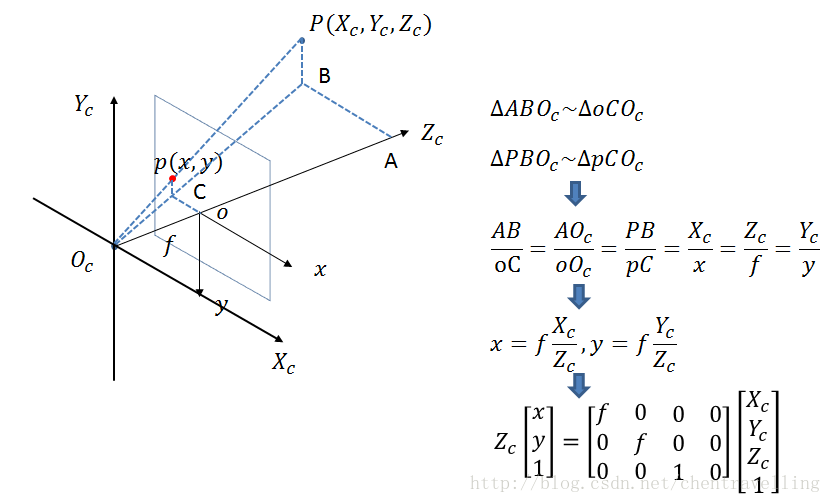
二、相機座標系到影象物理座標系

從相機座標系到影象座標系，屬於透視投影關係，從3D轉換到2D。 也可以看成是針孔模型的改變模型。滿足三角形的相似定理。

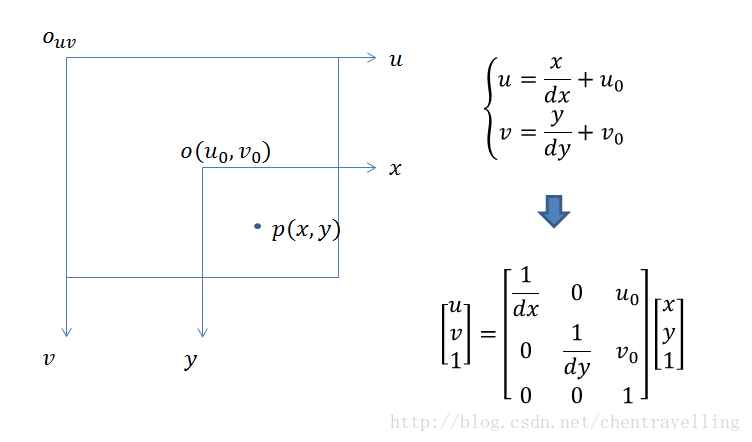
三、影象物理座標系到畫素座標系

此時與前面的座標系變換不同，此時沒有旋轉變換，但是座標原點位置不一致，大小不一致，則設計伸縮變換及平移變換。

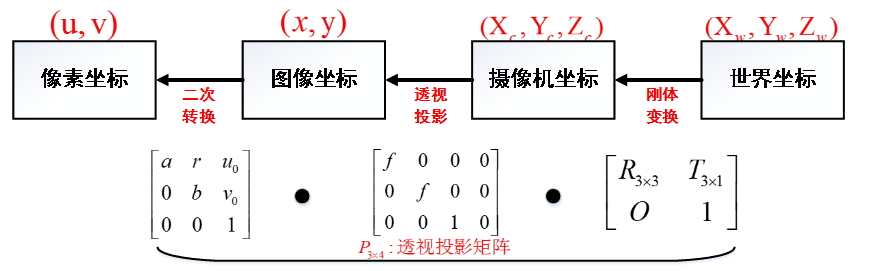
綜上所述，大家可以看出四個座標系之間存在著下述關係 ( 矩陣依次左乘 )：

其中相機的內參和外參可以通過張正友標定獲取。

通過最終的轉換關係來看，一個三維中的座標點，的確可以在影象中找到一個對應的畫素點。

但是反過來，通過影象中的一個點找到它在三維中對應的點就很成了一個問題，因為我們並不知道等式左邊的Zc的值。