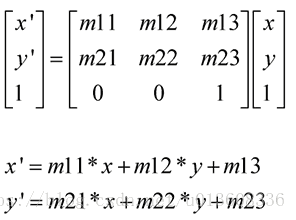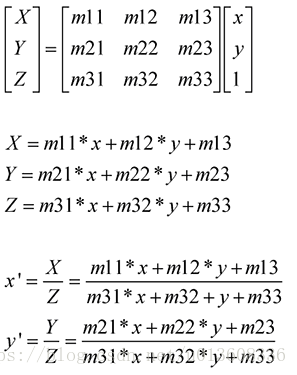線性,仿射,透視 變換
平面變換包括 線性變換,仿射變換
線性變換
線性變換包括 旋轉,映象(翻轉),伸縮(縮放),推移(錯切)
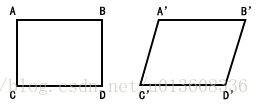
仿射變換
仿射變換 = 線性變換 + 平移
仿射變換是一種二維座標到二維座標之間的線性變換,它保持了二維圖形的“平直性”(直線經過變換之後依然是直線)和“平行性”(二維圖形之間的相對位置關係保持不變,平行線依然是平行線,且直線上點的位置順序不變)。任意的仿射變換都能表示為乘以一個矩陣(線性變換),再加上一個向量 (平移) 的形式
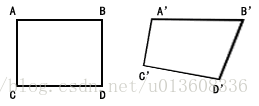
透視變換
透視變換是將圖片投影到一個新的視平面,也稱作投影對映.它是二維(x,y)到三維(X,Y,Z),再到另一個二維(x’,y’)空間的對映.透視變換是通過單應矩陣homography 實現的
參考
https://blog.csdn.net/andylei777/article/details/78333817
仿射和透視變換
相關推薦
線性,仿射,透視 變換
平面變換包括 線性變換,仿射變換 線性變換 線性變換包括 旋轉,映象(翻轉),伸縮(縮放),推移(錯切) 仿射變換 仿射變換 = 線性變換 + 平移 仿射變換是一種二維座標到二維座標之間的線性變換,它保持了二維圖形的“平直性”(直線經過變換之後依然是直線)和“平行性”(二
OpenCV中二維點求取進行仿射和透視變換之後的座標點方法
我使用的是OpenCV 2.2版本。得到了一個透視矩陣,想把螢幕上的一個二維點經過這個透視矩陣進行變換,本身很簡單的一個事情,卻頗費了一番周折。原因是剛接觸OpenCV,而且使用了OpenCV新新增的C++部分的矩陣類Mat,使用起來還真有點不順手,因為OpenCV中沒有向
等距變換(歐式變換),相似變換,仿射變換,射影變換
2維空間變換:維數(2*2) 1,等距變換 等距變換是,2維歐式空間變換 ,ε=1,等距變換是保向的,此時是歐氏變換(平移和旋轉的複合)。ε=−1,等距變換是逆向的。 簡單表示 R是正交矩陣。 自由度:3(該變換可以由兩組2D點確定,一組提供兩個自由度) 不
OpenCV2.4.13中warpAffine函式理解,旋轉,仿射變換,縮放,保持完整圖片
本文借鑑了這裡以及這裡的內容。 問題:為什麼寫這個東西? 答:在進行模板匹配的時候,發現一個問題,對於直接從圖片中摳出的模板,匹配效果較好,但是當模板發生形變的時候,效果就不理想了。 在對模板進行形變處理的時候,發現利用 warpAffine得到的結果並不
OpenCV計算機視覺學習(11)——影象空間幾何變換(影象縮放,影象旋轉,影象翻轉,影象平移,仿射變換,映象變換)
如果需要處理的原圖及程式碼,請移步小編的GitHub地址 傳送門:請點選我 如果點選有誤:https://github.com/LeBron-Jian/ComputerVisionPractice 影象的幾何變換是在不改變影象內容的前提下對影象畫素進行空間幾何變換,主要包括了影象的平移變換,縮放,
自定義聚集函式,仿wm_concat,使用CLOB,可處理超過4000長度字串
因開發需要,在使用wm_concat函式時,在字串長度超過4000後報錯,所以自定義一個類似的聚集函式,在內部使用CLOB處理,避免超長問題。 原始碼如下: 先以sys使用者授權: grant execute on dbms_lob to xxx; CREATE
射影變換與仿射變換、透視變換(射影既透視,包含了Z軸的資訊)
影象處理的仿射變換和透視變換(射影既透視,包含了Z軸的資訊)其實一直也沒理解“仿射”倆字是啥意思,但是大家都這麼叫,其實仿射變換和透視變換更直觀的叫法可以叫做“平面變換”和“空間變換”或者“二維座標變換”和“三維座標變換”。如果這麼命名的話,其實很顯然,這倆是一回事,只不過一
仿射函式,線性函式以及泰勒公式還有泰勒估算...
1. 先說仿射函式和線性函式 線性函式平常非常常見: 這裡我們是將一個4維的向量最後投射到一個1維的值。不過這裡注意,這個函式是經過原點的。 再看下仿射方程。 這裡我們可以看下他們的區別 直觀的區別就是會不會經過原點。 知乎上有大佬是這麼解釋“ 仿
已知仿射變換的係數,求仿射變換的反向係數
對於如下從(xx,yy)到(X,Y)的仿射變換: X = xx + ax * xx + bx * yy + cx Y = yy + ay * xx + by * yy + cy 已知(ax,bx,cx),(ay,by,cy)為其仿射變換系數,則(X,Y)到(
知源圖四點坐標和目標圖四點坐標,求透視變換矩陣
lan tails i++ show ffi 源碼 讓我 strong 函數 最近在搞圖像處理,碰到了透視變換的問題。 同事給我一些代碼,裏邊有誤差,挺嚴重,讓我幫他想想哪裏出錯了。搗鼓了很久,我猜測肯定是透視變換矩陣求錯了,然後我的透視變換之旅就開始了。
S1.3 仿射變換、透視變換、極座標對映演示
S1.3 仿射變換、透視變換、極座標對映演示 文章目錄 S1.3 仿射變換、透視變換、極座標對映演示 OpenCV影象變換示意表 仿射變換 透視變換 極座標對映 OpenCV影象變換示意表
影象的仿射變換與透視變換研究
&nb
仿射變換與透視變換(也即射影變換)的直觀理解
仿射變換 仿射變換更直觀的叫法可以叫做「平面變換」或者「二維座標變換」。其計算方法為座標向量和變換矩陣的乘積,換言之就是矩陣運算。在應用層面,放射變換是影象基於3個固定頂點的變換 射影變換(也即射影變換) 透視變換更直觀的叫法可以叫做「空間變換」或者「三維座標變換」
影象處理二:仿射變換和透視變換
一、仿射變換(Affine Transformation) 放射變換(平面變換、二維座標變換):是空間直角座標系的變換,從一個二維座標變換到另一個二維座標,仿射變換是一個線性變換,保持了影象的“平行性”和“平直性”,即影象中原來的直線和
基於opencv的影象縮放,旋轉,透視變換。
工具程式碼: #define WARPSTEPSIZE 0.2; #define RESIZESTEPSIZE 0.1; #define ROTATESTEPSIZE 10; float g_H_value = 0; float g_resize_value = 0;
單應性變換、仿射變換、透視變換 很到位
單應性變換 如下圖所示的平面的兩幅影象。紅點表示兩幅影象中的相同物理點,我們稱之為對應點。這裡顯示了四種不同顏色的四個對應點 - 紅色,綠色,黃色和橙色。 一個Homography是一個變換(3×3矩陣),將一個影象中的點對映到另一個影象中的對應點。單應性變換其實就是一
【輔助駕駛】透視變換(包含鳥瞰圖、俯檢視、正檢視)小結_附仿射變換
一、目的 應用1:實現掃描功能,類似“掃描全能王APP” 應用2:輔助駕駛(行車記錄儀) 二、原理 1、仿射變換 1)定義: 仿射變換是一種二維座標到二維座標之間的線性變換。它保持了二維圖形的“平直性”(直線經過變換之後依然是直線)和“平行性”(二
【輔助駕駛】透視變換、仿射變換(包含鳥瞰圖、俯檢視、正檢視)[2]——俯檢視
一、效果 二、程式碼實現 1、python程式碼,基於opencv庫和imutils庫 來源:https://blog.csdn.net/qq_34199383/article/details/79571318 from imutils import perspect
iOS-矩陣與線性代數的關係____仿射變換
大多數人在高中,或者大學低年級,都上過一門課《線性代數》。這門課其實是教矩陣。 剛學的時候,還蠻簡單的,矩陣加法就是相同位置的數字加一下。 矩陣減法也類似。 矩陣乘以一個常數,就是所有位置都乘以這個數。 但是,等到矩陣乘以矩陣的時候,一切就不一樣了。
仿射變換與透視變換
Mat M=Mat::eye(3,3, CV_32FC1); float alpha=PI/6; float tx=0; float ty=0; float scale=1; M.at<float>(0, 0) = cos(alpha); M.at<floa