仿射變換與透視變換(也即射影變換)的直觀理解
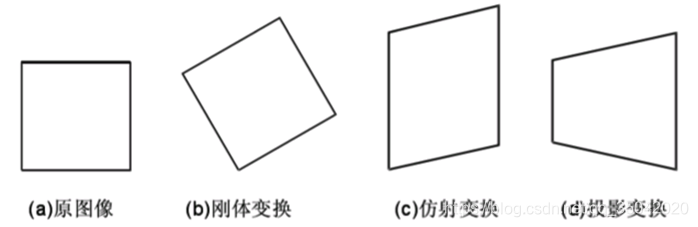
仿射變換
仿射變換更直觀的叫法可以叫做「平面變換」或者「二維座標變換」。其計算方法為座標向量和變換矩陣的乘積,換言之就是矩陣運算。在應用層面,放射變換是影象基於3個固定頂點的變換
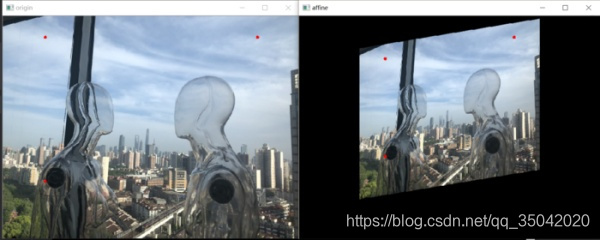
射影變換(也即射影變換)
透視變換更直觀的叫法可以叫做「空間變換」或者「三維座標變換」。圖中紅點即為固定頂點,在變換先後固定頂點的畫素值不變,影象整體則根據變換規則進行變換同理,透視變換是影象基於4個固定頂點的變換
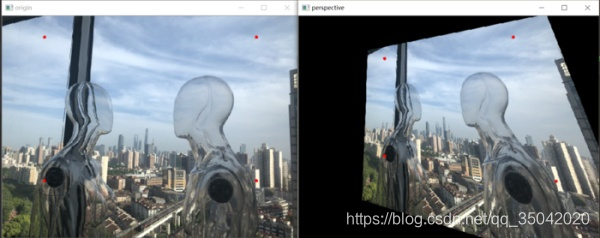
為什麼射影變換也叫透視變換呢?讀者可以想象一個原本方形的地板磚,在照片當中是什麼樣子。它不再是方形,甚至不是平等四邊形,而是一個不規則 的四邊形。所以射影變換也叫透視變換。
相關推薦
仿射變換與透視變換(也即射影變換)的直觀理解
仿射變換 仿射變換更直觀的叫法可以叫做「平面變換」或者「二維座標變換」。其計算方法為座標向量和變換矩陣的乘積,換言之就是矩陣運算。在應用層面,放射變換是影象基於3個固定頂點的變換 射影變換(也即射影變換) 透視變換更直觀的叫法可以叫做「空間變換」或者「三維座標變換」
影象的仿射變換與透視變換研究
&nb
仿射變換與透視變換
Mat M=Mat::eye(3,3, CV_32FC1); float alpha=PI/6; float tx=0; float ty=0; float scale=1; M.at<float>(0, 0) = cos(alpha); M.at<floa
正交投影變換與透視投影
相機投影模型 三維計算機圖形學的基本問題之一就是三維觀察問題:即如何把三維場景投影到要顯示的二維影象。大多數經典的解決投影變換方法有兩種:正交投影變換和透視投影變化。 正交投影變換用一個長方體來取景,並把場景投影到這個長方體的前面。這個投影不會有透視收縮效果
仿射集與凸集
tag 最小 sub span 特殊性 演示 clas imageview view 1.?概述 從這裏開始,為了復習所學知識,也是為了更加深刻地探討優化理論中的相關知識,所以將凸優化中的基礎概念做一個整理,然後形成一個凸優化系列隨筆。本系列將涉及部分數學推導,強調理論性,
射影變換與仿射變換、透視變換(射影既透視,包含了Z軸的資訊)
影象處理的仿射變換和透視變換(射影既透視,包含了Z軸的資訊)其實一直也沒理解“仿射”倆字是啥意思,但是大家都這麼叫,其實仿射變換和透視變換更直觀的叫法可以叫做“平面變換”和“空間變換”或者“二維座標變換”和“三維座標變換”。如果這麼命名的話,其實很顯然,這倆是一回事,只不過一
線性,仿射,透視 變換
平面變換包括 線性變換,仿射變換 線性變換 線性變換包括 旋轉,映象(翻轉),伸縮(縮放),推移(錯切) 仿射變換 仿射變換 = 線性變換 + 平移 仿射變換是一種二維座標到二維座標之間的線性變換,它保持了二維圖形的“平直性”(直線經過變換之後依然是直線)和“平行性”(二
S1.3 仿射變換、透視變換、極座標對映演示
S1.3 仿射變換、透視變換、極座標對映演示 文章目錄 S1.3 仿射變換、透視變換、極座標對映演示 OpenCV影象變換示意表 仿射變換 透視變換 極座標對映 OpenCV影象變換示意表
影象處理二:仿射變換和透視變換
一、仿射變換(Affine Transformation) 放射變換(平面變換、二維座標變換):是空間直角座標系的變換,從一個二維座標變換到另一個二維座標,仿射變換是一個線性變換,保持了影象的“平行性”和“平直性”,即影象中原來的直線和
單應性變換、仿射變換、透視變換 很到位
單應性變換 如下圖所示的平面的兩幅影象。紅點表示兩幅影象中的相同物理點,我們稱之為對應點。這裡顯示了四種不同顏色的四個對應點 - 紅色,綠色,黃色和橙色。 一個Homography是一個變換(3×3矩陣),將一個影象中的點對映到另一個影象中的對應點。單應性變換其實就是一
【輔助駕駛】透視變換(包含鳥瞰圖、俯檢視、正檢視)小結_附仿射變換
一、目的 應用1:實現掃描功能,類似“掃描全能王APP” 應用2:輔助駕駛(行車記錄儀) 二、原理 1、仿射變換 1)定義: 仿射變換是一種二維座標到二維座標之間的線性變換。它保持了二維圖形的“平直性”(直線經過變換之後依然是直線)和“平行性”(二
【輔助駕駛】透視變換、仿射變換(包含鳥瞰圖、俯檢視、正檢視)[2]——俯檢視
一、效果 二、程式碼實現 1、python程式碼,基於opencv庫和imutils庫 來源:https://blog.csdn.net/qq_34199383/article/details/79571318 from imutils import perspect
iOS-矩陣與線性代數的關係____仿射變換
大多數人在高中,或者大學低年級,都上過一門課《線性代數》。這門課其實是教矩陣。 剛學的時候,還蠻簡單的,矩陣加法就是相同位置的數字加一下。 矩陣減法也類似。 矩陣乘以一個常數,就是所有位置都乘以這個數。 但是,等到矩陣乘以矩陣的時候,一切就不一樣了。
【OpenCV3影象處理】仿射變換 透視變換
影象處理的仿射變換和透視變換 仿射變換和透視變換更直觀的叫法可以叫做“平面變換”和“空間變換”。一個是二維座標(x,y),一個是三維座標(x,y,z) 仿射變換:二維平面的變換 ; 線性變換 ;已知3對座標點就可以求得變換矩陣 透視變換:三維空間的變換
OpenCV中二維點求取進行仿射和透視變換之後的座標點方法
我使用的是OpenCV 2.2版本。得到了一個透視矩陣,想把螢幕上的一個二維點經過這個透視矩陣進行變換,本身很簡單的一個事情,卻頗費了一番周折。原因是剛接觸OpenCV,而且使用了OpenCV新新增的C++部分的矩陣類Mat,使用起來還真有點不順手,因為OpenCV中沒有向
單應性變換、仿射變換、透視變換
單應性變換 如下圖所示的平面的兩幅影象。紅點表示兩幅影象中的相同物理點,我們稱之為對應點。這裡顯示了四種不同顏色的四個對應點 - 紅色,綠色,黃色和橙色。 一個Homography是一個變換(3×3矩陣),將一個影象中的點對映到另一個影象中的對應點。單應性變
透視變換和仿射變換(下)
其實說白了仿射變換是透視變換的特殊形式,只不過透視變換的角度擴充套件到了z座標,相當於從空間中另一個平面看這個圖,仿射變換在同一個平面不同角度看同一個圖,一下是透視變換的一個例子,通過一個原圖(一個原圖,一個做了相應變換的圖),來確定變換的方位,思想還是上節的思想: 1.通
AGG第十八課 agg::trans_affine仿射變換
agg agg::trans_affine 仿射變換1 affine仿射變換概念在幾何上定義為兩個向量空間之間的一個仿射變換或者仿射映射(來自拉丁語,affinis,"和。..相關")由一個線性變換接上一個平移組成。2 agg::trans_affine成員函數說明2.1 縮放inline const t
Halcon 學習筆記3 仿射變換
continue use net example handle region blog enter this 像素的減少 開運算(較少) 腐蝕(去除更多) 對灰度圖像的開運算或腐蝕 相當於將灰度圖像變暗 像素增加 閉運算(較少) 膨脹(較多) 對灰度圖像的閉運算或膨脹
對圖像的仿射變換
控制 lan 換來 存儲 input 順序存儲 矩陣 bubuko war 仿射變換,又稱仿射映射,是指在幾何中,一個向量空間進行一次線性變換並接上一個平移,變換為另一個向量空間 線性變換包含了平移,縮放,旋轉,鏡像,斜切,正交投影,線性變換在幾何上可能造成拉伸但是不會直線
