線性迴歸——代價函式
Training Set
訓練集
| Size in feet2(x) | Price in 1000's(y) |
| 2104 | 460 |
| 1416 | 232 |
| 1534 | 315 |
| 852 | 178 |
Hypothesis:
\[{h_\theta }\left( x \right) = {\theta _0} + \theta {x}\]
Notation:
θi's: Parameters
θi
How to choose θi's?
如何選擇θi's?

Idea: Choose θ0, θ1so that h(x) is close to y for our training examples(x, y)
思想:對於訓練樣本(x, y)來說,選擇θ0,θ1 使h(x) 接近y。
minimize(θ0, θ1)\[\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {{x^{(i)}}} \right) - {y^i}} \right)}^2}} \]
選擇合適的(θ0, θ1)使得 \[\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {{x^{(i)}}} \right) - {y^i}} \right)}^2}} \] 最小。
為了使公式的數學意義更好,將公式改為 \[\frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {{x^{(i)}}} \right) - {y^i}} \right)}^2}} \]
這並不影響 (θ0, θ1)的取值。
定義代價函式(Cost function) \[J\left( {{\theta _0},{\theta _1}} \right) = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {{x^{(i)}}} \right) - {y^i}} \right)}^2}} \]
目標是 \[\mathop {\min imize}\limits_{{\theta _0},{\theta _1}} J\left( {{\theta _0},{\theta _1}} \right)\]
這個代價函式也稱為平方誤差代價函式(Squared error function)
總結:
Hypothesis: \[{h_\theta }\left( x \right) = {\theta _0} + \theta {x}\]
Parameters: (θ0, θ1)
Cost Functions: \[J\left( {{\theta _0},{\theta _1}} \right) = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {{x^{(i)}}} \right) - {y^i}} \right)}^2}} \]
Goal: \[\mathop {\min imize}\limits_{{\theta _0},{\theta _1}} J\left( {{\theta _0},{\theta _1}} \right)\]
例子幫助理解
首先令 θ0=0,則代價函式變為 \[J\left( {{\theta _1}} \right) = \frac{1}{{2m}}\sum\limits_{i = 1}^m {{{\left( {{h_\theta }\left( {{x^{(i)}}} \right) - {y^i}} \right)}^2}} \]
| hθ(x) | J(θ1) |
| 對於給定θ1的情況,它是x的函式 | 是θ1的函式 |
三個訓練樣本
| x | y |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
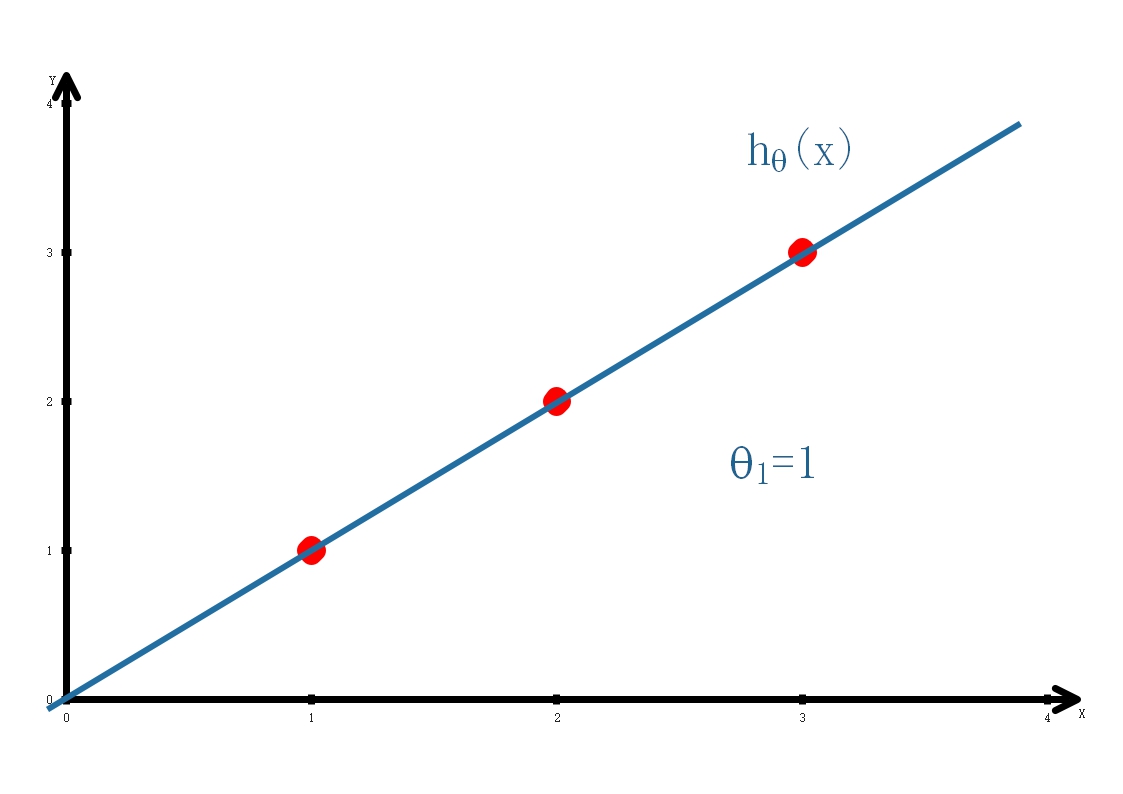
當θ1=1時,\[J\left( {{\theta _1}} \right) = \frac{1}{{2m}}\left( {{0^2} + {0^2} + {0^2}} \right) = 0\]
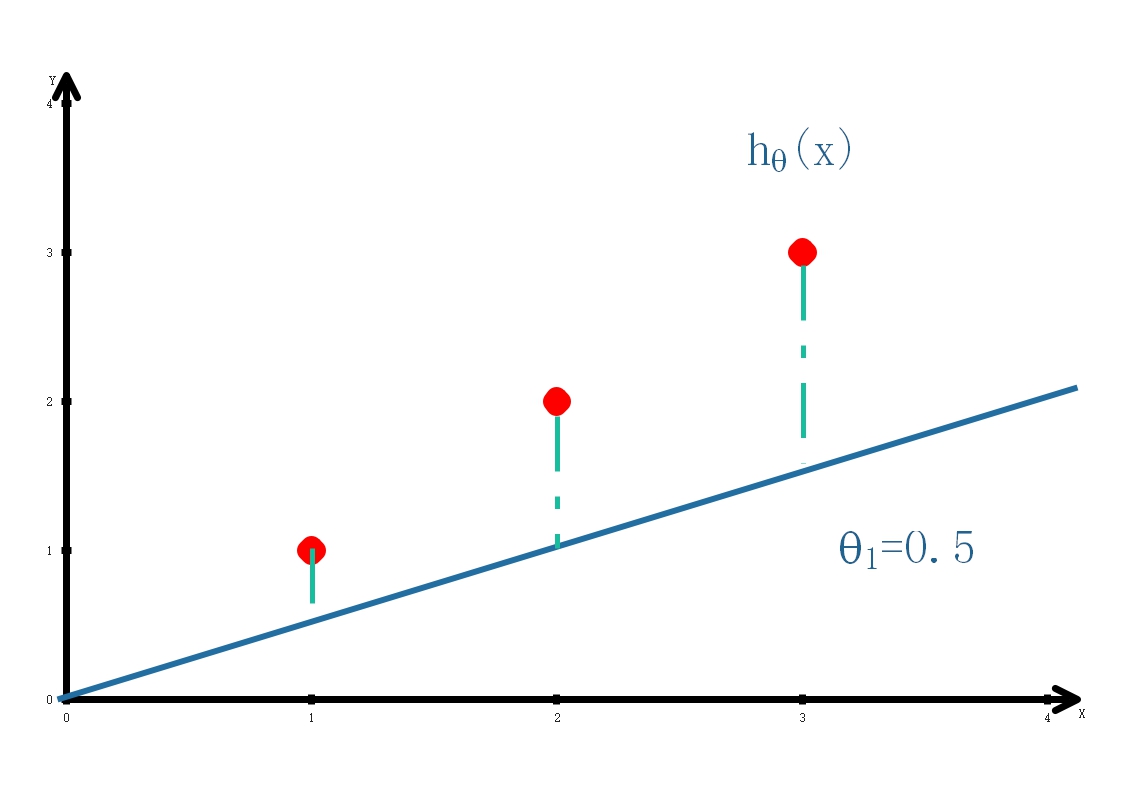
當θ1=0.5時,\[J\left( {0.5} \right) = \frac{1}{{2*3}}\left( {{{\left( {0.5 - 1} \right)}^2} + {{\left( {{\rm{1 - 2}}} \right)}^2} + {{\left( {{\rm{1}}{\rm{.5 - 3}}} \right)}^2}} \right) \approx {\rm{0}}{\rm{.58}}\]

θ1取不同值J(θ1)的值
每一個不同θ1的對應一條直線,我們的目的是找出最合適的θ1(最適合的直線)
