文章目錄

• 整除
• 同餘
• 質數
• Eratosthenes 篩法（埃氏篩法）
• 線性篩法
• 唯一分解定理
• 威爾遜定理
• 費馬小定理
• GCD
• 拓展歐幾里得定理
• 快速冪
• 排列問題
• 加法原理
• 乘法原理
• 容斥原理：
• 楊輝三角與二項式定理
• 線性代數
• 線性方程組與矩陣
• 線性方程組的初等變換
• 增廣矩陣
• 行階梯矩陣
• 行最簡形矩陣
• 行向量，列向量
• 對角矩陣
• 數量矩陣
• 單位矩陣
• 上三角矩陣
• 同型矩陣
• 矩陣的乘法運算
• 反對稱矩陣
• 可逆矩陣
• 分塊矩陣
• 矩陣的初等變換
• 行列式
• 行列式的定義

整除

設a是非零整數，b是整數。如果存在一個整數q，使得b=a*q那麼就說b可被a整除，記作a|b，且稱b是a的倍數,a是6的約數(因子)。
整除具有以下一些性質:

如果a|b且b|c,那麼alc。

設m=0,那麼a|b等價於(ma)|(m6)。
證明:因為aln且b|n
根據性質3可得:(a6)(bn) (a6)1(a+n)
再由性質2可得:(ab)1(anx+bnv)
其中:anz+bny=n*(az+by)=n1=n
5.若b=qd+c,那麼d1b的充要條件是dIc。

若數a其末位能被2整除則2|a
若數a其末兩位能被4整除則4|a
若數a其末三位能被8整除則8|a
若3能整除各位數之和，則這個數被3整除
若9能整除各位數之和，則這個數被9整除
若11能整除a的偶數位數字之和與奇數位數字之和的差，
若這個數末三位數與末三位之前的數字所組成的數字之差能被7，11，13整除，則這個數能被7，11，13整除

同餘

同餘問題比較有趣，涉及到很多的定理，首先要了解他的最基本的幾大性質

1 反身性 a≡a (mod m)
2 對稱性 若a≡b(mod m)，則b≡a (mod m)
3 傳遞性 若a≡b (mod m)，b≡c (mod m)，則a≡c (mod m)
4 同餘式相加 若a≡b (mod m)，c≡d(mod m)，則a±c≡b±d(mod m)
5 同餘式相乘 若a≡b (mod m)，c≡d(mod m)，則ac≡bd (mod m)

質數

質數是因數只有自己及其本身的數，他的判定很多，首先是最簡單的直接列舉因子

bool prima(int x) {
	FOR(i,2,sqrt(n)) 
	    if(n%i==0) return false;
	return true;
}

如果遇到大量的使用，這種演算法就顯得非常的慢，我們有埃氏篩法和線性篩法

Eratosthenes 篩法（埃氏篩法）

       試除法對於判定單個整數是否為質數具有較高的效率，但對於求1~N之間的所有質數問題，則複雜度過高（O（N）），當N較大時時間效率不太理想，因此引入埃氏篩法。
Eratosthenes 篩法的基本思路是：根據質數定義，既然質數無法被1和其本身之外任何數整除，那麼反之，對於任意整數M，其倍數顯然不是質數，對於N範圍內的數，篩掉這些數，留下的即為質數。具體步驟如下：

（1）假設2~N內所有數都是質數，並進行標記。 （2）從當前序列中選出最小的數並篩掉它的倍數。
（3）重複第2步，直到篩掉N內所有合數。具體過程如下（以20以內的質數篩法為例）：
2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20
2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20
2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20

       可以看到，對於N=20以內的質數篩選，只需要篩掉2~以內的倍數，即可得到結果。其時間複雜度為O（N log logN）。
具體程式碼如下：

void prime(int n){
		for(int i=2;i<=n;i++)a[i]=true;
		for(int i=2;i<=sqrt(n);i++)
 			if(a[i])
			  for(int j=i*i;j<=n;j+=i) a[j]=false;
		for(int i=2;i<=n;i++)
  			if(a[i])cout<<a[i];
	}

線性篩法

       儘管埃氏篩法已經非常優秀，但在篩選過程中仍然存在重複篩選的情況，比如12，被2篩掉後被3又篩一次，這導致其複雜度僅僅是接近線性而不是線性的（O（N））。因此，解決重複篩選問題，能顯著提升演算法的效率。
        線性篩法的基本思路是：讓合數僅被最小質因子篩選一次。以12為例，既可以表示為12=26，也可以表示為12=34，為了達到僅被篩一次的目的，我們需要在篩選的時候儲存合數的最小質因子，以確保合數在被最小質因子篩選後不會重複被其他質因子篩選（保證篩選的唯一性）。具體步驟如下：

（1）a陣列用來儲存當前的最小質因子，即a[i]=i的最小質因子（2≤i≤N），初始值均為0；p陣列用來儲存質數，初始值均為0；
（2）列舉i由2~n,當i為質數時，將i存入p陣列。
（3）用當前i分別乘以p陣列的每一個質因子（倍增），並標記a[ip[j]]=pj，特別的，當ip[j]>n（超出篩選範圍）或者p[j]>ai時，應跳出迴圈，否則就會出現重複篩選的情況。

例如，當i=4時，此時p[1]=2,p[2]=3;a[4]=2(因為被2篩選過);ip[j]有42和43兩種情況，因為a[4]=2,所以應當保留42使得a[8]=2(8被篩掉),而中斷43的情況，因為12需要被i=6時用p[1]=2來篩選掉。
       總而言之，要保證n=pq時p是最小質因子，應儘可能保證q比較大的時候才將n篩掉，這樣p就會盡可能小，例如12=2*6，應儘可能保證q=6時才篩選掉，這樣保證其最小質因子是2，而不是3（質因子3不要多管閒事）。具體程式碼如下：

void prime(int n){   //a 陣列記錄最小質因子，p陣列記錄質數
	int tot=0;
	memset(a,0,sizeof(a));
	for(int i=2;i<=n;i++){
	  if(a[i]==0){
	  	a[i]=i;
	  	p[++tot]=i;  
	  }
	  for(int j=1;j<=tot;j++){
	    if(p[j]>a[i] || i*p[j]>n) break; // 如果倍增的質因子比當前儲存的最小質因子大，或者倍增的數已經超出n的範圍，則跳出；
	    a[i*p[j]]=p[j];	
	  }
	}  
	for(int i=1;i<=tot;i++)cout<<p[i]<<" "; //輸出所有質數
}

關於質數還有很多的定理

唯一分解定理

定義：**任何一個大於1的自然數N，都可以唯一分解成有限個質數的乘積**，記為：	

p₁^c1p₂^c2p₃^c3…p_n^cn

其中pi均為質數，ci均為正整數，且滿足p1<p2<…<pm。
其中p1=2,c1=2,p2=3,c2=1。這樣的分解稱為標準分解式。
應用：
（1）一個大於1的正整數N，如果它的標準分解式為：p₁^c1p₂^c2p₃^c3…p_n^cn
，那麼它的正因數個數為（1+c¹）（1+c²）（1+c³）…（1+cⁿ）。
（2）N的全體正因數之和為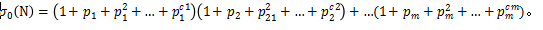

威爾遜定理

定義：若p為質數，
。
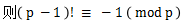此定理可逆，即對於某一正整數P，若有，則p一定是質數。

費馬小定理

定義：若p為質數，a為正整數，且p和a互質，則：p!。
	應用：我們可以利用費馬小定理來簡化冪模運算：由於，所以  有迴圈節，長度為p-1，所以

素數判定：
根據費馬小定理，我們可以任取若干個a，然後用費馬小定理進行判定，在a取得較多的前提下，該演算法出錯的機率很低。

尤拉定理
定義：若正整數a，p互質，則，其中為尤拉函式，表示正整數1~p中小於p且與p互質的數的個數(包含1)。

於正整數N，代表小於等於N的與N互質的數的個數，記作φ(N)
φ(N) = n*(1-1/p1)(1-1/p2)···
引理1:如果n為某一個素數p，則φ§=p-1;
引理2:如果n為某一個素數p的冪次，那麼φ(p^a)=(p-1)*p(a-1)
引理3:如果n為任意兩個數a和b的積，那麼φ(ab)=φ(a)*φ(b)

int euler(int n){ 		//返回euler(n)   
     int res=n,p=n;  
     for(int i=2;i<=sqrt(p);i++){  
         if(p%i==0){  
             res=res/i*(i-1); 
             while(p%i==0) p/=i;  
         }  
     }  
     if(p>1) res=res/p*(p-1);  
     return res;  
}

判斷素數由此有個一個新的方法，那就是用費馬小定理隨機，隨機個幾十次，幾百次，幾千次。。。他的精度就是很高的了

GCD

       gcd就是常見的最大公因數問題，gcd在algorithm庫中有一個自己的函式，__gcd(a,b)。通常手寫也是很容易的，運用歐幾里得定理：gcd(a,b)==gcd(b,a%b)，也叫輾轉相除法

int gcd(int a,int b) {
    return b==0?a:gcd(b,a%b);   
}

拓展歐幾里得定理

運用拓展歐幾里得定理可以很容易的解方程
       對於ax≡g(mod b)該方程有解的條件是gcd(a,b)|g，且解的個數為g / gcd(a,b)，對於該方程，我們可以先兩邊約分，得到ax≡1(mod b)的式子，解出該方程的解x，設t=gcd(a,b)，則其他解為xt、xt2…下面我們討論如何解ax≡1(mod b)
我們將ax≡1(mod b)轉化為ax+by=1，那麼對於方程bx+(a mod b)y=1,我們可以將它轉化為bx+(a-(a div b)b)y=1，即ay+b(x-(a / b)y)=1.這樣我們就可以遞迴求解。
由於a、b互質，最後一定會變成1x+0y=1的情況，這時我們令x=1，y=0。

int extend_gcd(int a,int b,int &x,int &y) {
    if(b==0) {
        x=1;
        y=0;
        return a;
    }
    int r=extend_gcd(b,a%b,y,x);
    y-=x*(a/b);
    return r;
}

安利一波毒瘤題目 P2398 GCD SUM

for i=1 to n for j=1 to n
sum+=gcd(i,j) 給出n求sum. gcd(x,y)表示x,y的最大公約數.

題目就是這麼短，乍一看非常簡單，隨手打了個簡單的程式碼，就準備上交

FOR(i,1,n) { 
   sum+=i; FOR(j,i+1,n)sum+=2*__gcd(i,j);
}
cout<<sum;

       還好我當時沒交，隨手算一下不是要T到飛起（後來試了一下果然是30分emmm資料還算良心）
正確做法是什麼呢，雖然程式碼一樣的短

for(ll i=n;i;--i){
    f[i]=n/i*(n/i);
    for(ll j=i<<1;j<=n;j+=i)f[i]-=f[j];
    ans+=f[i]*i;
}
printf("%lld",ans);

emmm毒瘤題目。。。原理數學太差講不出來（等我能講出來了一定要把這個更新了）

快速冪

快速冪這一個部分我最初掌握的不太好，導致扣了很多分，後來仔細的學習了一下
他的程式碼是這個樣子的

#define ll long long
ll quick(ll a,int b,ll c) {
    ll ans=1;
    while(b)  {
        if(b&1!=0) ans=(ans*a)%c;
        b>>=1;a=(a*a)%c;
    }
    return ans;
} 

這樣，可以使計算的數量大大縮小

排列問題

加法原理

：
做一件事有n種方法，第i種方法有pi種方案，則一共有p1+p2+…+pn種方案
互不影響的事件之間通常使用加法原理

乘法原理

做一件事有n個步驟，第i個步驟有pi種方案，則一共有p1p2…*pn種方案，

乘法原理是加法原理的特殊情況。二者都可以用於遞推。

注意：
使用加法原理的關鍵是分類：各類別之間必須不重不漏
如果有重複，我們可以使用容斥原理

容斥原理：

簡單來說：|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|B∩C|-|A∩C|+|A∩B∩C|
其中左邊是所有集合的∪，右邊是集合的各種搭配，每個搭配都是若干集合的交集
且每一項前面的正負號取決於集合的個數——奇數個數為+，偶數個數為-

這是很重要的一個公式

注意：
如果我們現在要求100以內能被4,5,6整除的數字的個數
根據公式得到：

ans=（100以內能被4整除的數字）+（能被5整除的數字）+（6整除的數字） -（能被20整除的數字）-（能被30整除的數字）-（能被12整除的數字） +（能被60整除的數字）

楊輝三角與二項式定理

組合數C(n,m)在組合數學中佔據著重要的位置，
與組合學相關的兩個最重要的兩個內容就是楊輝三角和二項式定理

首先我們先說說組合數C
（一下我們討論的都是從n和中選m個的組合）

公式： C(n,m)=n!/(m!*(n-m)!)

ta的重要性質如下：

C(n，0)=C(n，n)=1
C(n，m)=C(n，n-m)
C(n，k)+C(n，k+1)=C(n+1，k+1)
C(n，k+1)=C(n，k)*(n-k)/(k+1)

下圖就是楊輝三角啦：

另一方面，我們把(a+b)^n展開：

(a+b)^0=1 (a+b)^1=a+b
(a+b)^2=a2+2ab+b^2
(a+b)^3=a3+3a^2*b+3*a*b2+b^3
(a+b)^1=a4+4a^3*b+6*a2*b^2+4*a*b3+b^4

係數正好和楊輝三角一致
一般的，有二項式定理：

給定n，我們要怎麼求出a和b的所有項的係數呢
一個方法是遞推，運用楊輝三角中發現的規律：

c[1][0]=1; c[1][1]=1;
FOR(i,2,n){
    c[i][0]=1; c[i][i]=1;
    FOR（j,2,i-1) c[i][j]=c[i-1][j]+c[i-1][j-1];
}

然而這個演算法是n^2的，非常不優秀
另一個方法是利用公式：

c(n,k)=c(n,k-1)*(n-k+1)/k

從c(n,0)=1開始推

c[0]=1;
FOR(i,1,n) c[i]=c[i-1]*(n-i+1)/i;

線性代數

線性方程組與矩陣

線性方程組的初等變換

含義：

交換兩個方程次序，用一個非零常數乘以某個方程，用一個數乘一個方程後加到另一個方程上係數矩陣，方程組左端的係數排成的數表稱為係數矩陣

增廣矩陣

將方程組右側的常數新增到係數矩陣上稱為增廣矩陣

行階梯矩陣

特點：

可畫出一條階梯線，線的下方元素均為0
每個臺階只有一行，階梯豎線後面的第一個元素不為0，這樣的矩陣稱為行階梯矩陣

行最簡形矩陣

特點：

除了滿足行階梯矩陣的特點外，還滿足：每個非零行的首個元素為1，且這些元素所在的列的其他元素都為0

行向量，列向量

對角矩陣

特點：

除了左上角到右下角的直線（稱為主對角線）上的元素外的元素全是0，常記為diag(λλ1,λλ2,……,λλn)

數量矩陣

當對角矩陣的對角元素全部相等時，稱為n階數量矩陣

單位矩陣

數量矩陣的主對角線上的元素全為1時，稱為n階單位矩陣

上三角矩陣

主對角線下方的元素全為0時

同型矩陣

行數和列數分別相同的矩陣

矩陣的加法運算和數乘運算
加法滿足交換律和結合律；數乘滿足分配律結合律交換律

矩陣的乘法運算

矩陣的乘法不滿足交換律和消去律
(AB)k ≠ AkBk, (A+B)2 ≠A2+2AB +B2， （A+B)(A-B) ≠ A2-B2。只有當A,B可交換時，上述各式的等號才成立
矩陣的m次多項式
1.f(A)=a0+a1A+a2A2+…+amAm
2.性質：

矩陣的任何兩個矩陣多項式可交換
如果A=diag(λλ1,λλ2,……,λλn)，則f(A)=diag(f(λλ1),f(λλ2),……,f(λλn))
轉置矩陣
運算律：

(AT)T=A (A+B)
T=ATBT (λλA)
T=λλAT (AB)
T=BTAT

對稱矩陣

AT=A

對稱矩陣的基本性質：

設A是一個m××n矩陣，則AAT和ATA都是對稱矩陣
設A,B為n階對稱陣，則AB為對稱陣的充要條件是A與B可交換

反對稱矩陣

AT=-A

可逆矩陣

定義：設A與B是n階方陣，若AB=BA=E，則稱A是可逆的，B是A的逆矩陣
特性：
若A可逆，則A的逆矩陣唯一
對角矩陣ΛΛ=diag(λλ1,λλ2,……,λλn)是可逆的，且ΛΛ-1=diag(λλ1-1,λλ2-1,……,λλn-1)

運算律:

(A-1)-1=A
(AT)-1=(A-1)T
(λλA)-1=(1/λλ)A
(AB)-1=B-1A-1

分塊矩陣

定義:我們將矩陣A用一些縱線和橫線分成若干個小矩陣，每個小矩陣稱為A的子塊，以子塊為元素的形式上的矩陣稱為分塊矩陣

分塊矩陣的運算:

分塊矩陣的加法：設A，B為同型矩陣，且採用相同的分塊法，則類似於矩陣的加法 分塊矩陣的數乘：類似於矩陣的數乘 分塊矩陣的乘法:
類似於矩陣的乘法 分塊矩陣的轉置：類似於矩陣的轉置，不過不但要將行列互換，而且行列互換後的各子塊都要相應進行轉置
分塊矩陣的逆運算：分塊對角矩陣的逆運算和對角矩陣的逆運算類似。若 D= {ACOB} {AOCB}

則D−1D−1= {A−1−B−1CA−1OB−1} {A−1O−B−1CA−1B−1}

矩陣的初等變換

初等行變換:

交換兩行
以非零實數乘以某行
將某行乘以一個常數加到另一行上
初等列變換:

交換兩列
以非零實數乘以某列
將某列乘以一個常數加到另一列上
矩陣等價
矩陣A通過有限次初等行（列）變換為矩陣B，稱矩陣A與B行（列）等價，記為A→rBA→rB(A→cBA→cB)，如果A通過有限次初等行變換與初等列變換化為矩陣B，稱A與B等價，記為A→BA→B
矩陣等價具有自反性，對稱性，傳遞性

標準型
{ErOOO}
{ErOOO}
稱為矩陣的標準型,左上角是一個單位矩陣
任一矩陣都等價於一個標準型
初等矩陣
定義：對單位矩陣實行一次初等變換後所得到的矩陣稱為初等矩陣

E(i,j)表示ri↔rjri↔rj或ci↔cjci↔cj
E(i(k))表示ri×kri×k 或ci×kci×k
E(i,j(k))表示riri+krjrj或cjcj+kcici
初等矩陣的逆矩陣：

• E(i,j)−1E(i,j)−1=E(i,j)
• E(i(k))−1E(i(k))−1=E(i(k−1k−1))
• E(i,j(k))−1E(i,j(k))−1= E(i,j(-k))

other:初等矩陣左乘A表示初等行變換，EA
初等矩陣右乘A表示初等列變換，AE

利用初等行變換求逆矩陣
A−1A−1(A|E)=(E|A−1A−1)
即把(A|E)通過初等行變換變成左邊是E，則右邊就是A的逆矩陣了

行列式

行列式的定義

二階與三階行列式
∣∣∣a11a21a12a22∣∣∣=a11a22−a12a21
|a11a12a21a22|=a11a22−a12a21

稱為由二階方陣A所確定的二階行列式，即為D，還可即為detA或|A|
∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣=a11a22a33+a12a23a31+a21a32a13−a13a22a31−a12a21a33−a23a32a11
|a11a12a13a21a22a23a31a32a33|=a11a22a33+a12a23a31+a21a32a13−a13a22a31−a12a21a33−a23a32a11
餘子式
MijMij為行列式D中劃去元素aijaij所在的第i行，第j列後，餘下的(n−1)2(n−1)2 個元素按照原來的位置次序構成的 n-1 階行列式，稱為元素aijaij 的餘子式

代數餘子式
Aij=(−1)i+jMijAij=(−1)i+jMij 稱為元素aijaij 的代數餘子式

多階行列式
n階矩陣A的行列式D=detA=|A|可表示為它的任一行(列）的各元素與其對應的代數餘子式乘積之和，即D=ai1Ai1+ai2Ai2+…+ainAin=a1jA1j+a2jA2j+…+anjAnjD=ai1Ai1+ai2Ai2+…+ainAin=a1jA1j+a2jA2j+…+anjAnj
(i=1,2,…,n)(j=1,2,…,n)

Tips:若行列式中某行（列）中有較多的零元素，則按該行（列）展開能簡化計算

2.2行列式的性質
行列式的7大性質
性質1：D=DTD=DT，即行列式與它的轉置行列式相等
性質2：互換行列式的兩行（列），行列式變號
性質3：用k乘以行列式的某一行(列）得到的行列式等於原來的行列式的k倍
性質4：若行列式的某一行（列）的元素都是兩數之和，則該行列式等於兩個行列式的和。比如
∣∣∣∣a11a21+b21a31a12a22+b22a32a13a23+b23a33∣∣∣∣=∣∣∣∣a11a21a31a12a22a32a13a23a33∣∣∣∣+∣∣∣∣a11b21a31a12b22a32a13b23a33∣∣∣∣
|a11a12a13a21+b21a22+b22a23+b23a31a32a33|=|a11a12a13a21a22a23a31a32a33|+|a11a12a13b21b22b23a31a32a33|
性質5：若將行列式的某一行（列）乘以數k加到另一行（列），則行列式的值不變

性質6：行列式中的第i行（列）元素與第j行（列）（j≠ij≠i）對應元素的代數餘子式乘積之和為0
性質7：設A，B為n階方陣，C為m階方陣，則
1.|ATAT|=|A|
2.|λλA|=λnλn|A|
3.
∣∣∣ADOC∣∣∣=|A||C|
|AODC|=|A||C|

∣∣∣ODAC∣∣∣=(−1)mn|A||C|
|OADC|=(−1)mn|A||C|

4.|AB|=|A| |B|
推論:1.行列式如果有兩行（列）元素成比例，則此行列式等於零。
2.若行列式中某行（列）的元素全為零，則此行列式等於零

Tips:計算行列式時，若行列式D中的每一行（列）中的元素之和相同，則可將各列（行）加到第一列（行）提取公因子。

範德蒙德行列式
Dn=∣∣∣∣∣∣∣∣1x1x21…xn−111x2x22…xn−12…1xnx23…xn−1n∣∣∣∣∣∣∣∣=∏n≥i>j≥1(xi−xj)
Dn=|11…1x1x2…xnx12x22…x32…x1n−1x2n−1…xnn−1|=∏n≥i>j≥1(xi−xj)
2.3行列式的應用
克拉默（Cramer）法則
如果線性方程組的係數行列式D≠≠0,則方程組有唯一解
xj=DjDxj=DjD
其中DjDj是把行列式D中的第j列替換成方程Ax=b中的b

一些定理
如果線性方程組無解或有兩個不同的解，則它的係數行列式必為零
如果齊次線性方程組的係數行列式為D ≠≠ 0,則齊次線性方程組只有零解
若其次線性方程組有非零解，則它的係數行列式必為零
伴隨矩陣
定義:設A=（aij)n×nA=（aij)n×n, 元素a_{ij}的代數餘子式AijAij按如下的順序構成一個n階矩陣
Dn=∣∣∣∣∣∣A11A12…A1nA21A22…A2n…An1An2…Ann∣∣∣∣∣∣
Dn=|A11A21…An1A12A22…An2…A1nA2n…Ann|

稱為矩陣A的伴隨矩陣，記為A∗A∗
注意：並不是aijaij的位置直接放AijAij，還要經過轉置
定理:

定理2.6：AA∗=A∗A=|A|EAA∗=A∗A=|A|E
推論1：A−1=A∗|A|A−1=A∗|A|
推論2：|A−1|=1|A||A−1|=1|A|
推論3：(A∗)−1=A|A|(A∗)−1=A|A|
推論4：A∗=|A|A−1A∗=|A|A−1
推論5：(A∗)−1=(A−1)∗(A∗)−1=(A−1)∗
矩陣的秩
子式的定義:在m×nm×n階矩陣A中任取k行k列（k≤m,k≤nk≤m,k≤n）,位於這些行列式交叉處的k2k2個元素，不改變它們在A中所處的位置次序而得到的k階行列式，稱為A的k階子式

矩陣的秩：設在矩陣A中有一個不等於0的r階子式D，且所有r+1階子式（如果存在的話）全等於0，那麼D稱為矩陣A的最高階非零子式，數r稱為矩陣A的秩，記作R(A)，並規定若A=O，則R(A)=0

滿秩矩陣：顯然，R(A)≤min{m,n}R(A)≤min{m,n}，若R(A)=min{m,n}，稱A為滿秩矩陣

矩陣的秩的性質
性質1：R(AT)=R(A)R(AT)=R(A)
性質2：設A經過初等變換得到B，則R(A)=R(B)
性質3：設A為m×nm×n矩陣，則R(A)=r的衝要條件是A的標準型為
∣∣∣ErOOO∣∣∣m×n
|ErOOO|m×n
,其中ErEr為r階單位陣
性質4：設Am×n,Bn×s,Ct×nAm×n,Bn×s,Ct×n
(1)若R(A)=n（此時稱A為列滿秩），則R(AB)=R(B)
(2)若R(A)=m（此時稱A為行滿秩），則R(CA)=R©
性質5：
(1)設Am×n,Bm×sAm×n,Bm×s，則max{R(A),R(B)}≤≤R(A,B)≤≤R(A)+R(B)
(2)設Am×n,Bm×nAm×n,Bm×n，則R(A+B)≤≤R(A)+R(B)
(3設Am×n,Bn×sAm×n,Bn×s，則R(A)+R(B)-n≤≤R(AB)≤≤min{R(A),R(B)}
性質6：設A為n階方陣，則