質數

 1 bool prime(int q)
 2 {
 3     if(q==2||q==3) return 1;
 4     if(q==1) return 0;
 5     if(q%6!=1||q%6!=5) return 0;
 6     int cnt=sqrt(q);
 7     for(int i=5;i<=cnt;i+=6)
 8         if(q%2!=0||q%(i+2)!=0) return 0;
 9     return 1;
10 }

 1 //埃氏篩 篩出1~n的素數 
 2 void prime_select()
 3 {
 
 4     for(int i=2;i<=n;i++)
 5     {
 6         if(vis[i]) continue;
 7         printf("%d\n",i);
 8         for(int j=n;j<=n/i;j++) vis[i*j]=1;
 9     } 
10 } 

線性篩還是要學的qwq（真香），它的原理是每個合數會被它的最小質因子篩一次，利用了當前已經篩出的質數。複雜度真·O（N）

 1 //線性篩
 2 void prime_select()
 3 {
 4     //v[]記錄下標數的最小質因子 初值為0 
 5     for
 
(int i=2;i<=n;i++)
 6     {
 7         if(v[i]==0) v[i]=i,prime[++m]=i;
 8         for(int j=1;j<=m;j++)
 9         {//i是比prime[j]更小的質因子or超出n的範圍 
10             if(prime[j]>v[i]||prime[j]>n/i) break;
11             v[i*prime[j]]=prime[j];
12         }
13     }
14 }

 1 //質因數分解--基於算術基本定理 複雜度O（根號n）
 

 2 void divide()
 3 {
 4     for(int i=2;i<=sqrt(n);i++)
 5         if(n%i==0)
 6         {
 7             p[++m]=i;c[m]=0;
 8             while(n%i==0) n/=i,c[m]++;
 9         }
10     if(n>1) p[++m]=n,c[m]=1;
11     for(int i=1;i<=m;i++)
12         printf("%d^%d\n",p[i],c[i]); 
13 } 

丟幾個例題跑嚶嚶嚶

例題1 LuoguP1865 A%B Problem ---（本部落格開通不久的舊文）

　　　因為資料範圍較水，僅1e6，所以我們可以先使用線性篩篩出素數。區間個數用字首和維護。它珂以當做一個練線性篩的不錯模板題。

例題2 UVA10140 Prime Distance  --（題解一篇）

　　　我們知道，任意一個合數x一定包含不超過sqrt(n)的質因子。

　　　所以我們就篩出2~sqrt(R)之間的所有素數，用他們來標記全部範圍內的合數。最後沒被標記的數就是質數，比較相鄰的質數位置取最大。

例題3 階乘分解 沒有題面，口胡一下。

　　　把N！分解質因數，按算術基本定理的形式輸出。（N為1e6級別）

　　　N！中質因數p的個數就等於1~N每個數含質因子p的個數之和。其他...詳見lyd書p131，不會用LaTex，懶得打了...

　　　時間複雜度O（Nlogn）

約數

//　　這樣寫書式的複習我肯定幹不完...以後會簡潔一點...（真香）

• 基於算術基本定理，N的正約數集合個數為(a1+1)*(a2+1)*(a3+1)*........*(an+1）（基於乘法原理）（$a_i$為算術基本定理中的各指數）
• 求1~N每個數的正約數集合--倍數法

//求1~N每個數的正約數集合--倍數法
void work()
{
    vector<int>fac[500010];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n/i;j++)
            fac[i*j].push_back(i);
}

複雜度為O（N+N/2+N/3+N/4+...+N/N）=O（NlogN）（調和級數）

例題1 LuoguP1463反素數

例題2 LuoguP2261餘數之和

• $gcd(a,b)*lcm(a,b)=a*b$

int gcd(int a,int b)
{
    return b ? gcd(b,a%b) : a;
}//輾轉相除
int gcd(int a,int b)
{
    while(a!=b)
    {
        if(a>b)
            a-=b;
        else 
            b-=a;
    }
    return a;
}//更相減損

• 尤拉函式：1~n中與n互質的數的個數

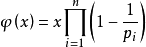
• 1~n中與n互質的數的個數為$n*φ(n)/2$
• 若a,b互質，則φ(a)φ(b)=φ(ab)。
• 若n為質數，φ(n)=n-1

void phi()
{
    phi[1]=1;
    for(int i=2;i<=n;i++) phi[i]=i;
    for(int i=2;i<=n;i++)
        if(phi[i]==i)
            for(int j=i;j<=n;j+=i)
                phi[j]=phi[j]/i*(i-1);
} 

• 費馬小定理：當p為質數時候， a^(p-1)≡1(mod p)
• exgcd：https://www.cnblogs.com/nopartyfoucaodong/p/9514767.html