題目描述
小淵和小軒是好朋友也是同班同學，他們在一起總有談不完的話題。一次素質拓展活動中，班上同學安排做成一個 mm 行 nn 列的矩陣，而小淵和小軒被安排在矩陣對角線的兩端，因此，他們就無法直接交談了。幸運的是，他們可以通過傳紙條來進行交流。紙條要經由許多同學傳到對方手裡，小淵坐在矩陣的左上角，座標 (1,1(1,1 )，小軒坐在矩陣的右下角，座標 (m,n)(m,n) 。從小淵傳到小軒的紙條只可以向下或者向右傳遞，從小軒傳給小淵的紙條只可以向上或者向左傳遞。

在活動進行中，小淵希望給小軒傳遞一張紙條，同時希望小軒給他回覆。班裡每個同學都可以幫他們傳遞，但只會幫他們一次，也就是說如果此人在小淵遞給小軒紙條的時候幫忙，那麼在小軒遞給小淵的時候就不會再幫忙。反之亦然。

還有一件事情需要注意，全班每個同學願意幫忙的好感度有高有低（注意：小淵和小軒的好心程度沒有定義，輸入時用 00 表示），可以用一個 0-1000−100 的自然數來表示，數越大表示越好心。小淵和小軒希望儘可能找好心程度高的同學來幫忙傳紙條，即找到來回兩條傳遞路徑，使得這 22 條路徑上同學的好心程度之和最大。現在，請你幫助小淵和小軒找到這樣的 22 條路徑。

輸入輸出格式
輸入格式：
輸入檔案，第一行有 22 個用空格隔開的整數 mm 和 nn ，表示班裡有 mm 行 nn 列。

接下來的 mm 行是一個 m \times nm×n 的矩陣，矩陣中第 ii 行 jj 列的整數表示坐在第 ii 行 jj 列的學生的好心程度。每行的 nn 個整數之間用空格隔開。

輸出格式：
輸出檔案共一行，包含一個整數，表示來回 22 條路上參與傳遞紙條的學生的好心程度之和的最大值。

輸入輸出樣例
輸入樣例#1： 複製
3 3
0 3 9
2 8 5
5 7 0
輸出樣例#1： 複製
34

題解：
感覺很難理解…直到看到了這個題解。

因為是從上方和從下方傳紙條，為了方便，我們相當於從左上角連續傳兩張紙條，路徑不重複，效果相同。

從左上來看的話就只能向右或向下傳紙條。

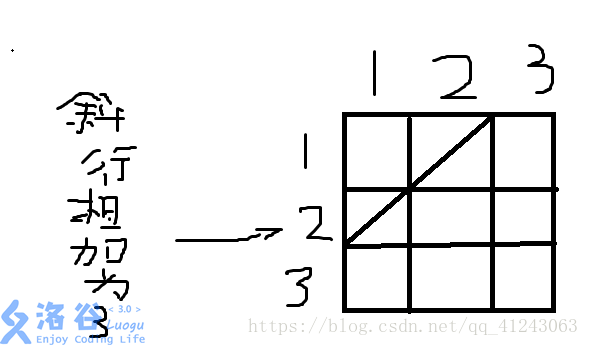
那麼兩張紙條在過程中就一定在一條斜線上，而在一條斜線上縱座標與橫座標相加相等。
在如圖的斜線中，兩個點的和都為3.

首先重要的就是三維F陣列。

第一維度維護的是在傳的過程中縱座標與橫座標的和。

在同一斜線上，剩下表示兩個點的從座標就可以表示這兩個點的位置。
第二維度維護的是相對在左邊的點的縱座標。

第三維度維護的是相對在右邊的點的縱座標。

當查詢一個情況時，只有四種情況可以到他

F[sum][i][j]=max{F[sum-1][i][j]+F[k-1][i][j-1]+F[k-1][i-1][j]+F[k-1][i-1][j-1]；

最後再加上a數組裡存的兩個點的好感度即可

程式碼：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=60;
int a[maxn][maxn];
int F[2*maxn][maxn][maxn];
int main()
{
  int m,n;
  scanf("%d%d",&m,&n);
  for(int i=1;i<=m;i++)
    for(int j=1;j<=n;j++)
      scanf("%d",&a[i][j]);
  //F[sum][i][j]=max{F[sum-1][i][j]...
  memset(F,-1,sizeof(F));//賦初值為-1 (原因在後面） 
  F[2][1][1]=0;//最初的點，在左上角，好感度為0 
  for(int k=3;k<m+n;k++)
    for(int i=1;i<n;i++)
      for(int j=i+1;j<=n;j++)
      {
        int s=F[k][i][j];
        if(F[k-1][i][j]>s)s=F[k-1][i][j];
        if(F[k-1][i-1][j]>s)s=F[k-1][i-1][j];
        if(F[k-1][i][j-1]>s)s=F[k-1][i][j-1];
        if(F[k-1][i-1][j-1]>s)s=F[k-1][i-1][j-1];
        if(s==-1)continue;//當s為-1時，說明四種情況都不能到該點，故不存在。 
        F[k][i][j]=s+a[k-i][i]+a[k-j][j];//該點的值為最大的前一個值與當前F[k][i][j]表示兩點的值的和。 
      }
  printf("%d",F[m+n-1][n-1][n]);//因為i永遠小於j，所以右下角的點不會求到，
  //但是到右下角只有一種情況，就是在右下角的上面和右下角的左邊，直接輸出就好了。 
  return 0;
 }