DQN從入門到放棄5 深度解讀DQN演算法
分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow
也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！
0 前言
如果說DQN從入門到放棄的前四篇是開胃菜的話，那麼本篇文章就是主菜了。所以，等吃完主菜再放棄吧！
1 詳解Q-Learning
在上一篇文章DQN從入門到放棄 第四篇中，我們分析了動態規劃Dynamic Programming並且由此引出了Q-Learning演算法。可能一些知友不是特別理解。那麼這裡我們再用簡單的語言描述一下整個思路是什麼。
為了得到最優策略Policy，我們考慮估算每一個狀態下每一種選擇的價值Value有多大。然後我們通過分析發現，每一個時間片的Q(s,a)和當前得到的Reward以及下一個時間片的Q(s,a)有關。有些知友想不通，在一個實驗裡，我們只可能知道當前的Q值，怎麼知道下一個時刻的Q值呢？大家要記住這一點，Q-Learning建立在虛擬環境下無限次的實驗。這意味著可以把上一次實驗計算得到的Q值拿來使用呀。這樣，不就可以根據當前的Reward及上一次實驗中下一個時間片的Q值更新當前的Q值了嗎？說起來真是很拗口。下面用比較形象的方法再具體分析一下Q-Learning。
Q-Learning的演算法如下：
對於Q-Learning，首先就是要確定如何儲存Q值，最簡單的想法就是用矩陣，一個s一個a對應一個Q值，所以可以把Q值想象為一個很大的表格，橫列代表s，縱列代表a，裡面的數字代表Q值，如下表示：
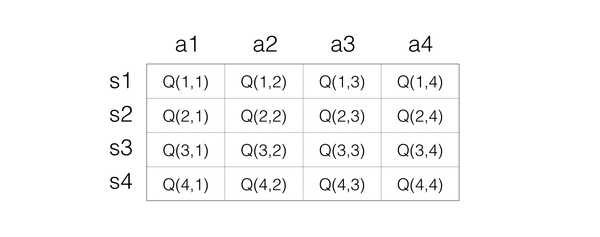這樣大家就很清楚Q值是怎樣的 了。接下來就是看如何反覆實驗更新。
Step 1：初始化Q矩陣，比如都設定為0
Step 2：開始實驗。根據當前Q矩陣及方法獲取動作。比如當前處在狀態s1，那麼在s1一列每一個Q值都是0，那麼這個時候隨便選擇都可以。
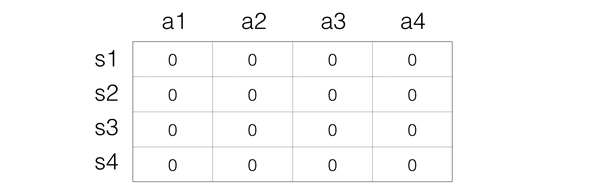假設我們選擇a2動作，然後得到的reward是1，並且進入到s3狀態，接下來我們要根據
來更新Q值，這裡我們假設是1，
所以在這裡，就是
那麼對應的s3狀態，最大值是0，所以,Q表格就變成：
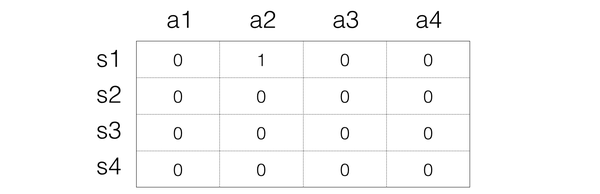Step 3：接下來就是進入下一次動作，這次的狀態是s3，假設選擇動作a3，然後得到1的reward，狀態變成s1，那麼我們同樣進行更新：
所以Q的表格就變成：
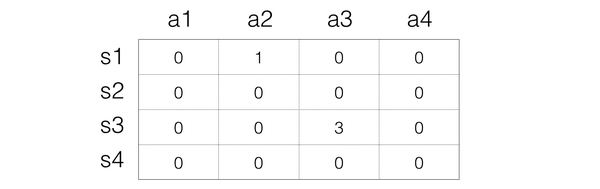
Step 4： 反覆上面的方法。
就是這樣，Q值在試驗的同時反覆更新。直到收斂。
相信這次知友們可以很清楚Q-Learning的方法了。接下來，我們將Q-Learning拓展至DQN。
2 維度災難
在上面的簡單分析中，我們使用表格來表示Q(s,a)，但是這個在現實的很多問題上是幾乎不可行的，因為狀態實在是太多。使用表格的方式根本存不下。
舉Atari為例子。
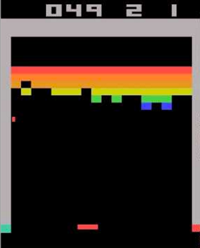計算機玩Atari遊戲的要求是輸入原始影象資料，也就是210x160畫素的圖片，然後輸出幾個按鍵動作。總之就是和人類的要求一樣，純視覺輸入，然後讓計算機自己玩遊戲。那麼這種情況下，到底有多少種狀態呢？有可能每一秒鐘的狀態都不一樣。因為，從理論上看，如果每一個畫素都有256種選擇，那麼就有：
這簡直是天文數字。所以，我們是不可能通過表格來儲存狀態的。我們有必要對狀態的維度進行壓縮，解決辦法就是 價值函式近似Value Function Approximation
3 價值函式近似Value Function Approximation
什麼是價值函式近似呢？說起來很簡單，就是用一個函式來表示Q(s,a)。即
f可以是任意型別的函式，比如線性函式：
其中
是函式f的引數。
大家看到了沒有，通過函式表示，我們就可以無所謂s到底是多大的維度，反正最後都通過矩陣運算降維輸出為單值的Q。
這就是價值函式近似的基本思路。
如果我們就用來統一表示函式f的引數，那麼就有
為什麼叫近似，因為我們並不知道Q值的實際分佈情況，本質上就是用一個函式來近似Q值的分佈，所以，也可以說是
4 高維狀態輸入，低維動作輸出的表示問題
對於Atari遊戲而言，這是一個高維狀態輸入（原始影象），低維動作輸出（只有幾個離散的動作，比如上下左右）。那麼怎麼來表示這個函式f呢？
難道把高維s和低維a加在一起作為輸入嗎？
必須承認這樣也是可以的。但總感覺有點彆扭。特別是，其實我們只需要對高維狀態進行降維，而不需要對動作也進行降維處理。
那麼，有什麼更好的表示方法嗎？
當然有，怎麼做呢？
其實就是，只把狀態s作為輸入，但是輸出的時候輸出每一個動作的Q值，也就是輸出一個向量
，記住這裡輸出是一個值，只不過是包含了所有動作的Q值的向量而已。這樣我們就只要輸入狀態s，而且還同時可以得到所有的動作Q值，也將更方便的進行Q-Learning中動作的選擇與Q值更新（這一點後面大家會理解）。
5 Q值神經網路化！
終於到了和深度學習相結合的一步了！
意思很清楚，就是我們用一個深度神經網路來表示這個函式f。
這裡假設大家對深度學習特別是卷積神經網路已經有基本的理解。如果不是很清楚，歡迎閱讀本專欄的CS231n翻譯系列文章。
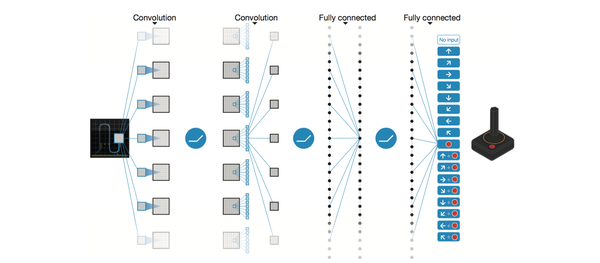以DQN為例，輸入是經過處理的4個連續的84x84影象，然後經過兩個卷積層，兩個全連線層，最後輸出包含每一個動作Q值的向量。
對於這個網路的結構，針對不同的問題可以有不同的設定。如果大家熟悉Tensorflow，那麼肯定知道建立一個網路是多麼簡單的一件事。這裡我們就不具體介紹了。我們將在之後的DQN tensorflow實戰篇進行講解。
總之，用神經網路來表示Q值非常簡單，Q值也就是變成用Q網路（Q-Network）來表示。接下來就到了很多人都會困惑的問題，那就是
怎麼訓練Q網路？？？
6 DQN演算法
我們知道，神經網路的訓練是一個最優化問題，最優化一個損失函式loss function，也就是標籤和網路輸出的偏差，目標是讓損失函式最小化。為此，我們需要有樣本，巨量的有標籤資料，然後通過反向傳播使用梯度下降的方法來更新神經網路的引數。
所以，要訓練Q網路，我們要能夠為Q網路提供有標籤的樣本。
所以，問題變成：
如何為Q網路提供有標籤的樣本？
答案就是利用Q-Learning演算法。
大家回想一下Q-Learning演算法，Q值的更新依靠什麼？依靠的是利用Reward和Q計算出來的目標Q值：
因此，我們把目標Q值作為標籤不就完了？我們的目標不就是讓Q值趨近於目標Q值嗎？
因此，Q網路訓練的損失函式就是
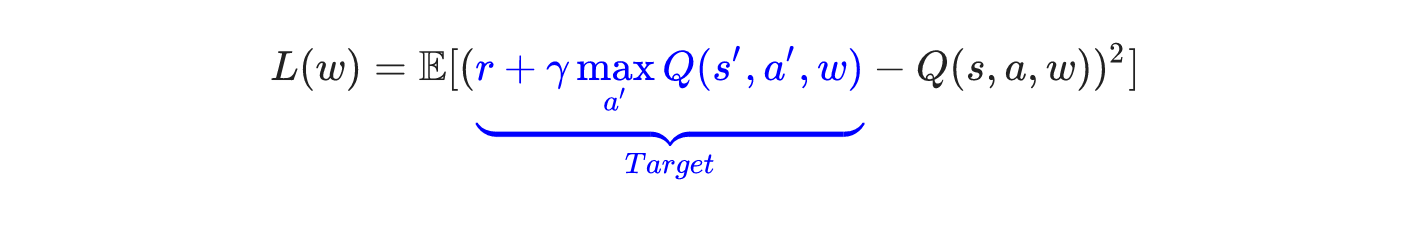上面公式是即下一個狀態和動作。這裡用了David Silver的表示方式，看起來比較清晰。
既然確定了損失函式，也就是cost，確定了獲取樣本的方式。那麼DQN的整個演算法也就成型了！
接下來就是具體如何訓練的問題了！
7 DQN訓練
我們這裡分析第一個版本的DQN，也就是NIPS 2013提出的DQN。
我們分析了這麼久終於到現在放上了DQN演算法，真是不容易。如果沒有一定基礎直接上演算法還真是搞不明白。
具體的演算法主要涉及到Experience Replay，也就是經驗池的技巧，就是如何儲存樣本及取樣問題。
由於玩Atari採集的樣本是一個時間序列，樣本之間具有連續性，如果每次得到樣本就更新Q值，受樣本分佈影響，效果會不好。因此，一個很直接的想法就是把樣本先存起來，然後隨機取樣如何？這就是Experience Replay的意思。按照腦科學的觀點，人的大腦也具有這樣的機制，就是在回憶中學習。
那麼上面的演算法看起來那麼長，其實就是反覆試驗，然後儲存資料。接下來資料存到一定程度，就每次隨機採用資料，進行梯度下降！
也就是
在DQN中增強學習Q-Learning演算法和深度學習的SGD訓練是同步進行的！
通過Q-Learning獲取無限量的訓練樣本，然後對神經網路進行訓練。
樣本的獲取關鍵是計算y，也就是標籤。
8 小結
好了，說到這，DQN的基本思路就介紹完了，不知道大家理解得怎麼樣？在下一篇文章中，我們將分析DQN在這一年來的發展變化！感謝知友們的關注！
文中圖片引用自
[1] Mnih, Volodymyr, et al. "Playing atari with deep reinforcement learning." arXiv preprint arXiv:1312.5602 (2013).
[2] Mnih, Volodymyr, et al. "Human-level control through deep reinforcement learning."Nature 518.7540 (2015): 529-533.
版權宣告：本文為原創文章，未經允許不得轉載！
給我老師的人工智慧教程打call！http://blog.csdn.net/jiangjunshow
