Feasibility of Learning

Learning is Impossible？

我們想要在D以外的資料中更接近目標函式似乎是做不到的，只能保證對D有很好的分類結果。機器學習的這種特性被稱為沒有免費午餐（No Free Lunch）定理。NFL定理表明沒有一個學習演算法可以在任何領域總是產生最準確的學習器。不管採用何種學習演算法，至少存在一個目標函式，能夠使得隨機猜測演算法是更好的演算法。

Probability to the Rescue

Connection to Learning

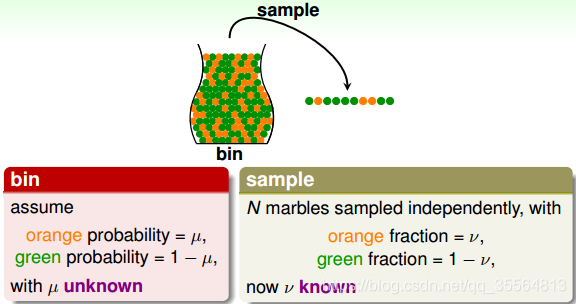
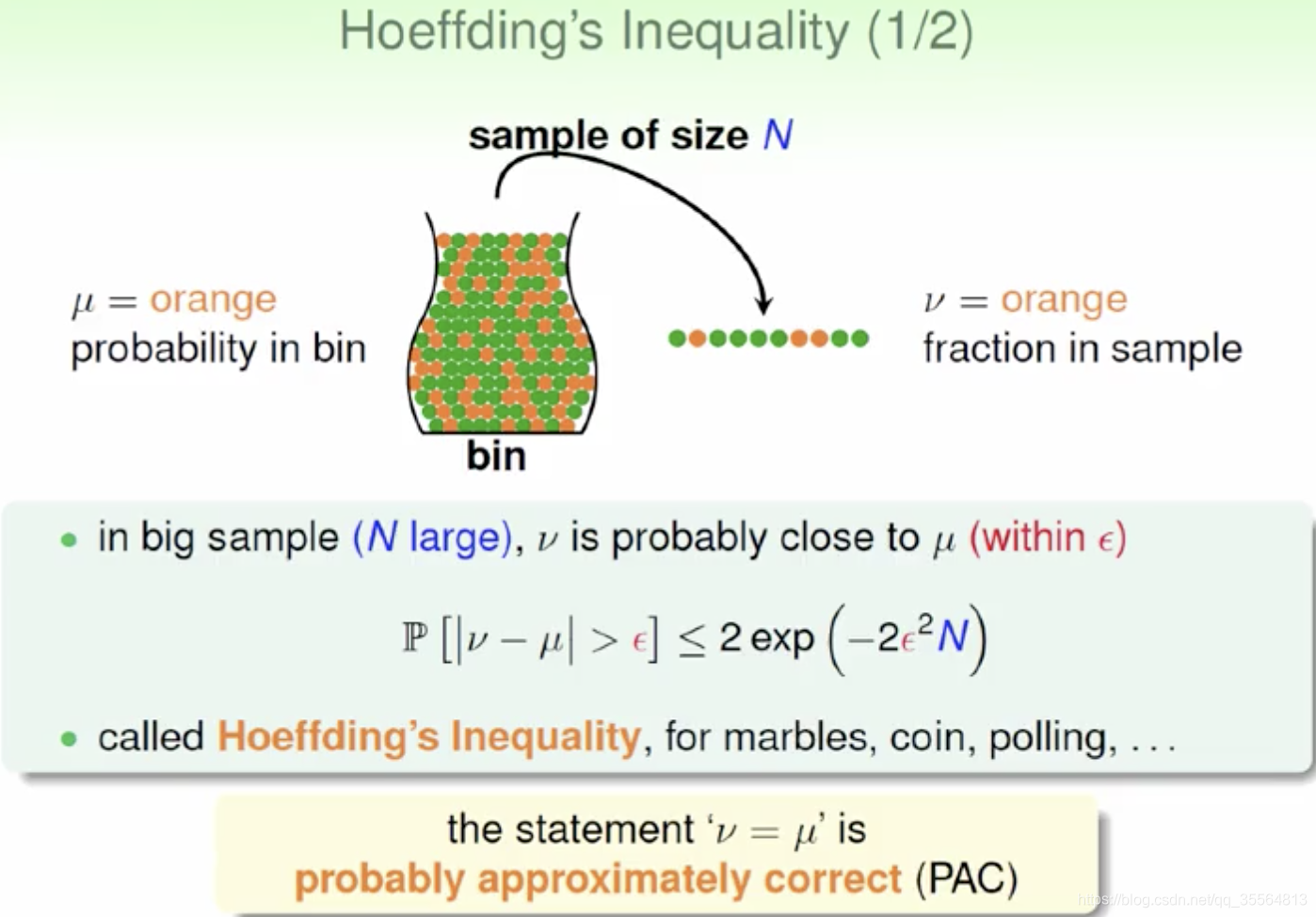
下面，我們將罐子的內容對應到機器學習的概念上來。機器學習中hypothesis與目標函式相等的可能性，類比於罐子中橙色球的概率問題；罐子裡的一顆顆彈珠類比於機器學習樣本空間的x；橙色的彈珠類比於h(x)與f不相等；綠色的彈珠類比於h(x)與f相等；從罐子中抽取的N個球類比於機器學習的訓練樣本D，且這兩種抽樣的樣本與總體樣本之間都是獨立同分布的。所以呢，如果樣本N夠大，且是獨立同分布的，那麼，從樣本中 $h$

這裡我們引入兩個值 $E_{in}(h$)和 $E_{out}(h)$。 $E_{in}(h)$表示在抽樣樣本中，h(x)與 $y_n$不相等的概率； $E_{out}(h)$表示實際所有樣本中，h(x)與f(x)不相等的概率是多少。

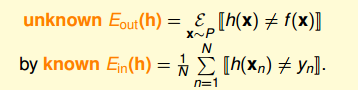
Connection to Real Learning

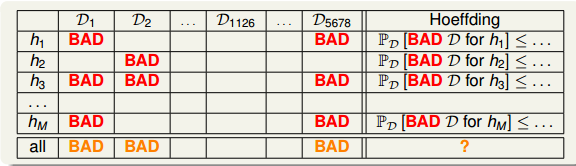
也就是說，不同的資料集 $D_n$，對於不同的hypothesis，有可能成為Bad Data。只要 $D_n$在某個hypothesis上是Bad Data，那麼 $D_n$就是Bad Data。只有當 $D_n$在所有的hypothesis上都是好的資料，才說明 $D_n$不是Bad Data，可以自由選擇演演算法A進行建模。那麼，根據Hoeffding’s inequality，Bad Data的上界可以表示為連級（union bound）的形式：

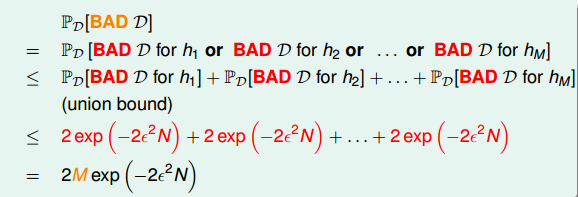
其中，M是hypothesis的個數，N是樣本D的數量， $\epsilon$是引數。該union bound表明，當M有限，且N足夠大的時候，Bad Data出現的概率就更低了，即能保證D對於所有的h都有 $E_{in}\approx E_{out}$，滿足PAC，演演算法A的選擇不受限制。那麼滿足這種union bound的情況，我們就可以和之前一樣，選取一個合理的演演算法（PLA/pocket），選擇使 $E_{in}$最小的 $h_m$作為g，一般能夠保證 $g\approx f$，即有不錯的泛化能力。

所以，如果hypothesis的個數M是有限的，N足夠大，那麼通過演演算法A任意選擇一個g，都有 $E_{in}\approx E_{out}$成立；同時，如果找到一個g，使 $E_{in}\approx 0$，PAC就能保證 $E_{out}\approx 0$。至此，就證明了機器學習是可行的。

但是如果M是無數個，例如之前介紹的PLA的直線具有無數條，那麼是否這些推論就不成立了呢？

總結

本節課主要介紹了機器學習的可行性。首先引入NFL定理，說明機器學習無法找到一個g能夠完全和目標函式f一樣。接著介紹了可以採用一些統計上的假設，例如Hoeffding不等式，建立 $E_{in}$和 $E_{out}$的聯絡，證明對於某個h，當N足夠大的時候， $E_{in}$和 $E_{out}$是PAC的。最後，對於h個數很多的情況，只要有h個數M是有限的，且N足夠大，就能保證 $E_{in}\approx E_{out}$，證明機器學習是可行的。