Coursera機器學習基石筆記week5
Training vs Testing
Recap and Preview
簡單回顧一下前面幾節課的內容:
- 第一節課,介紹了機器學習的定義,目標是找到最好的g,使g f,保證
- 第二節課,介紹瞭如何讓 ,即使用PLA、pocket algorithm來實現
- 第三節課,介紹了機器學習的分類
- 第四節課,介紹了機器學習的可行性,通過統計學知識,證明了在一些假設前提下,證明了
那麼總的來說機器學習就是為了使
當M很小的時候,由上節課介紹的霍夫丁不等式,得到 ,即能保證第一個核心問題成立。但M很小時,演演算法A可以選擇的hypothesis有限,不一定能找到使 足夠小的hypothesis,即不能保證第二個核心問題成立。當M很大的時候,同樣由霍夫丁不等式, 與 的差距可能比較大,第一個核心問題可能不成立。而M很大,使得演演算法A的可以選擇的hypothesis就很多,很有可能找到一個hypothesis,使 足夠小,第二個核心問題可能成立。
從上面的分析來看,M的選擇直接影響機器學習兩個核心問題是否滿足,M不能太大也不能太小。
Effective Number of Lines
如果平面上只有一個點x1,那麼直線的種類有兩種:一種將x1劃為+1,一種將x1劃為-1:
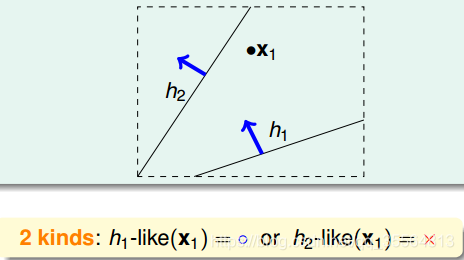
平面上有兩個點時,直線的種類有4種:
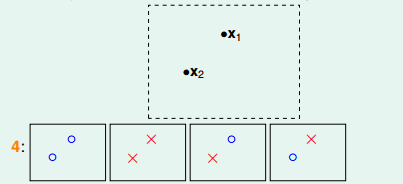
但是在平面有三個點的情況也會出現不能用一條直線劃分的情況:
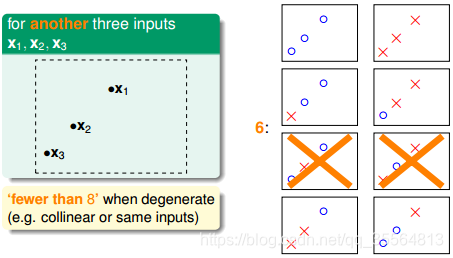
也就是說,對於平面上三個點,不能保證所有的8個類別都能被一條直線劃分。那如果是四個點x1、x2、x3、x4,我們發現,平面上找不到一條直線能將四個點組成的16個類別完全分開,最多隻能分開其中的14類,即直線最多隻有14種:
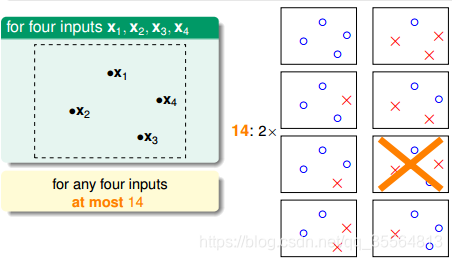

Effective Number of Hypotheses
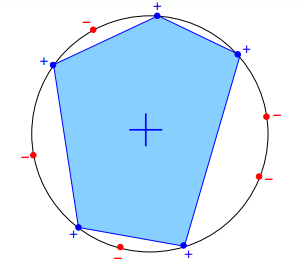
dichotomy(二分類)就是將空間中的點(例如二維平面)用一條直線分成正類(藍色o)和負類(紅色x)。令H是將平面上的點用直線分開的所有hypothesis h的集合,dichotomy H與hypotheses H的關係是:hypotheses H是平面上所有直線的集合,個數可能是無限個,而dichotomy H是平面上能將點完全用直線分開的直線種類,它的上界是 。接下來,我們要做的就是嘗試用dichotomy代替M。
成長函式(growth function),記為
。
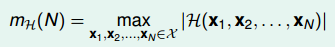
成長函式就是讓我們找最大的dichotomy。也就是找之前對應effective lines的數量最大值。
針對一維的Positive Rays:

若有N個點,則整個區域可分為N+1段,很容易得到其成長函式
。注意當N很大時,
,這是我們希望看到的
針對一維的Positive Intervals:

它的成長函式可以由下面推導得出:

上面的成長函式中,藍色的表示在N+1個節點中選擇兩個端點進行切割,兩個端點之間為+1即
,紅色的表示不選擇端點進行切割,即所有的節點都是-1.
這種情況下, ,在N很大的時候,仍然是滿足的。
再來看這個例子,假設在二維空間裡,如果hypothesis是凸多邊形或類圓構成的封閉曲線,如下圖所示,左邊是convex的,右邊不是convex的。那麼,它的成長函式是多少呢?
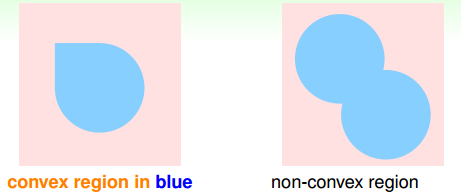
當資料集D按照如下的凸分佈時,我們很容易計算得到它的成長函式
。這種情況下,N個點所有可能的分類情況都能夠被hypotheses set覆蓋,我們把這種情形稱為shattered。也就是說,如果能夠找到一個數據分佈集,hypotheses set對N個輸入所有的分類情況都做得到,那麼它的成長函式就是
。
Break Point
我們已經知道:

對於2D perceptrons,我們之前分析了3個點,可以做出8種所有的dichotomy,而4個點,就無法做出所有16個點的dichotomy了。所以,我們就把4稱為2D perceptrons的break point(5、6、7等都是break point)。令有k個點,如果k大於等於break point時,它的成長函式一定小於2的k次方。
break point的定義就是使
的k的最小值。那麼根據該定義,我們可以得出:
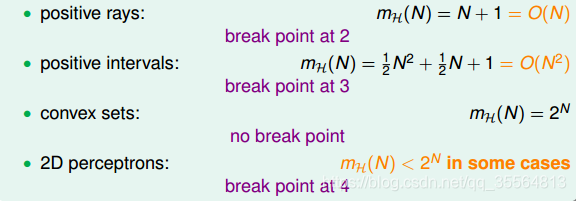
通過觀察,我們猜測成長函式可能與break point存在某種關係:對於convex sets,沒有break point,它的成長函式是2的N次方;對於positive rays,break point k=2,它的成長函式是O(N);對於positive intervals,break point k=3,它的成長函式是
。則根據這種推論,我們猜測2D perceptrons,它的成長函式
。如果成立,那麼就可以用
代替M,就滿足了機器能夠學習的條件。
總結
本節課,我們指出針對N個訓練資料,最多隻有 個hypothesis,由此引出了成長函式。針對不同的情況,成長函式也各有不同。對於我們學習的2D perceptrons,我們發現從某點開始是少於 次的。由此又引出break point的概念。
