樹結構大全
阿新 • • 發佈:2018-11-10
文章目錄
說明
示意圖
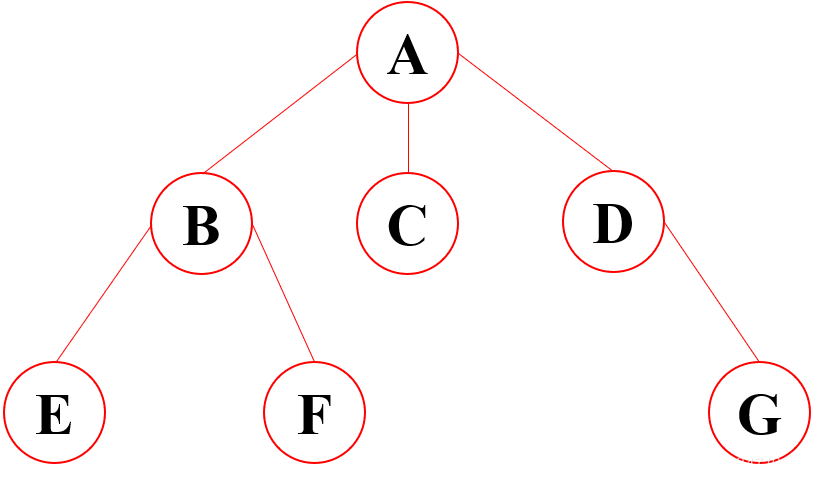
- 結點的度:結點擁有的子樹的數目。eg:結點 A 的度為3
- 樹的度:樹種各結點度的最大值。eg:樹的度為3
- 葉子結點:度為 0 的結點。g:E、F、C、G 為葉子結點
- 孩子結點:一個結點的子樹的根節點。eg:B、C、D 為 A 的子結點
- 雙親結點:B 為 A 的子結點,那麼 A 為 B 的雙親結點
- 兄弟結點:一個雙親結點結點的孩子互為兄弟結點。eg:B、C、D 為兄弟結點
- 結點的層次:根節點為第一層,子結點為第二層,依次向下遞推…eg:E、F、G 的層次均為 3
- 樹的深度:樹種結點的最大深度。eg:該樹的深度為 3
- 森林:m 棵互不相交的樹稱為森林
樹結構的性質
- 非空樹的結點總數等於樹種所有結點的度之和加 1
- 度為 K 的非空樹的第 i 層最多有 ki-1 個結點(i >= 1)
- 深度為 h 的 k 叉樹最多有(kh - 1)/(k - 1)個結點
- 具有 n 個結點的 k 叉樹的最小深度為 logk(n(k-1)+1))
二叉樹
二叉樹的定義
二叉樹是一種特殊的樹:它或者為空,或者由一個根節點加上根節點的左子樹和右子樹組成,這裡要求左子樹和右子樹互不相交,且同為二叉樹,很顯然,這個定義是遞迴形式的。
滿二叉樹與完全二叉樹
滿二叉樹: 如果一棵二叉樹的任意一個結點或者是葉子結點,或者有兩棵子樹,同時葉子結點都集中在二叉樹的最下面一層上,這樣的二叉樹稱為滿二叉樹
完全二叉樹: 若二叉樹中最多隻有最下面兩層結點的度小於 2 ,並且最下面一層的結點(葉子結點)都依次排列在該層最左邊的位置上,具有這樣結構特點的樹結構稱為完全二叉樹。

二叉樹的性質
- 在二叉樹中第 i 層上至多有 2i-1 個結點(i >=1)
- 深度為 k 的二叉樹至多有 2k-1 個結點(k >=1)
- 對於任何一棵二叉樹,如果其葉子結點數為 n0 ,度為 2 的結點數為 n2 ,那麼 n0 = n2 + 1
- 具有 n 個結點的完全二叉樹的深度為 log2n + 1
結點定義
typedef struct BiTNode{
ElemType data;
struct BiTNode * lchild, * rchild;
} BiTNode, *BiTree;
二叉樹的建立
/*建立一棵二叉樹*/
void CreatBiTree(BiTree *T) {
char c;
scanf("%c", &c);
if(c == ' ') *T = NULL;
else {
*T = (BiTNode * )malloc(sizeof(BiTNode)); /*建立根結點*/
(*T)->data = c; /*向根結點中輸入資料*/
CreatBiTree(&((*T)->lchild)); /*遞迴地建立左子樹*/
CreatBiTree(&((*T)->rchild)); /*遞迴地建立右子樹*/
}
}
二叉樹的遍歷
基於深度遍歷二叉樹
分為先序(DLR)、中序(LDR)、後序遍歷(LRD)
#include "stdio.h"
#include "malloc.h"
typedef struct BiTNode {
char data; /*結點的資料域*/
struct BiTNode *lchild, *rchild; /*指向左孩子和右孩子*/
} BiTNode, *BiTree;
/*建立一棵二叉樹*/
void CreatBiTree(BiTree *T) {
char c;
scanf("%c", &c);
if(c == ' ') *T = NULL;
else {
*T = (BiTNode * )malloc(sizeof(BiTNode)); /*建立根結點*/
(*T)->data = c; /*向根結點中輸入資料*/
CreatBiTree(&((*T)->lchild)); /*遞迴地建立左子樹*/
CreatBiTree(&((*T)->rchild)); /*遞迴地建立右子樹*/
}
}
/*前序遍歷二叉樹*/
void PreOrderTraverse(BiTree T ) {
if(T) { /*遞迴結束條件,T為空*/
printf("%3c", T->data); /*訪問根結點,將根結點內容輸出*/
PreOrderTraverse(T->lchild); /*先序遍歷T的左子樹*/
PreOrderTraverse(T->rchild); /*先序遍歷T的右子數*/
}
}
/*中序遍歷二叉樹*/
void InOrderTraverse(BiTree T) {
if(T) { /*如果二叉樹為空,遞迴遍歷結束*/
InOrderTraverse(T->lchild); /*中序遍歷T的左子樹*/
printf("%3c", T->data); /*訪問根結點*/
InOrderTraverse(T->rchild); /*中序遍歷T的右子數*/
}
}
/*後序遍歷二叉樹*/
void PosOrderTraverse(BiTree T) {
if(T) { /*如果二叉樹為空,遞迴遍歷結束*/
PosOrderTraverse(T->lchild); /*後序遍歷T的左子樹*/
PosOrderTraverse(T->rchild); /*後序遍歷T的右子數*/
printf("%3c", T->data); /*訪問根結點*/
}
}
int main() {
BiTree T = NULL; /*最開始T指向空*/
printf("Input some characters to create a binary tree\n");
CreatBiTree(&T); /*建立二叉樹*/
printf("The squence of preorder traversaling binary tree\n");
PreOrderTraverse(T); /*先序遍歷二叉樹*/
printf("\nThe squence of inorder traversaling binary tree\n");
InOrderTraverse(T); /*中序遍歷二叉樹*/
printf("\nThe squence of posorder traversaling binary tree\n");
PosOrderTraverse(T); /*後序遍歷二叉樹*/
getchar();
getchar();
}
基於層次遍歷二叉樹
方法一
#include "stdio.h"
typedef struct BiTNode {
char data; /*結點的資料域*/
struct BiTNode *lchild, *rchild; /*指向左孩子和右孩子*/
} BiTNode, *BiTree;
/*建立一棵二叉樹*/
void CreatBiTree(BiTree *T) {
char c;
scanf("%c", &c);
if(c == ' ') *T = NULL;
else {
*T = (BiTNode * )malloc(sizeof(BiTNode)); /*建立根結點*/
(*T)->data = c; /*向根結點中輸入資料*/
CreatBiTree(&((*T)->lchild)); /*遞迴地建立左子樹*/
CreatBiTree(&((*T)->rchild)); /*遞迴地建立右子樹*/
}
}
/*遍歷二叉樹*/
void PreOrderTraverse(BiTree T ) {
if(T) { /*遞迴結束條件,T為空*/
printf("%3c", T->data); /*訪問根結點,將根結點內容輸出*/
PreOrderTraverse(T->lchild); /*先序遍歷T的左子樹*/
PreOrderTraverse(T->rchild); /*先序遍歷T的右子數*/
}
}
void visit(BiTree p) {
printf("%3c", p->data);
}
void layerOrderTraverse(BiTree T) {
BiTree queue[20], p;
int front, rear;
if(T != NULL) {
queue[0] = T; /*將根結點的指標(地址)入佇列*/
front = -1;
rear = 0;
while(front < rear) { /*當佇列不為空時進入迴圈*/
p = queue[++front]; /*取出隊頭元素*/
visit(p); /*訪問p指向的結點元素*/
if(p->lchild != NULL) /*將p結點的左孩子結點指標入佇列*/
queue[++rear] = p->lchild;
if(p->rchild != NULL) /*將p結點的右孩子結點指標入佇列*/
queue[++rear] = p->rchild;
}
}
}
main() {
BiTree T = NULL; /*最開始T指向空*/
printf("Input some characters to create a binary tree\n");
CreatBiTree(&T); /*建立二叉樹*/
printf("\nThe squence of layerorder traversaling binary tree\n");
layerOrderTraverse(T);
getchar();
getchar();
}
方法二
void layerOrderTraverse(BiTree T){
BiTree p;
queue<BiTree> q;
if(T != NULL){
q.push(T);
while(!q.empty()){
p = q.front();
q.pop();
visit(p); // 自定義訪問操作
if(p->lchild != NULL)
q.push(p->lchild);
if(p->rchild != NULL)
q.push(p->rchild);
}
}
}
二叉樹的深度
方法一
#include "stdio.h"
#include "malloc.h"
typedef struct BiTNode{
char data; /*結點的資料域*/
struct BiTNode *lchild , *rchild; /*指向左孩子和右孩子*/
} BiTNode , *BiTree;
/*建立一棵二叉樹*/
void CreatBiTree(BiTree *T)
{
char c;
scanf("%c",&c);
if(c == ' ') *T = NULL;
else{
*T = (BiTNode * )malloc(sizeof(BiTNode)); /*建立根結點*/
(*T)->data = c; /*向根結點中輸入資料*/
CreatBiTree(&((*T)->lchild)); /*遞迴地建立左子樹*/
CreatBiTree(&((*T)->rchild)); /*遞迴地建立右子樹*/
}
}
/*計算二叉樹的深度*/
void getDepth(BiTree T,int n,int *level)
{
if(T!=NULL)
{
if(n> *level)
{
*level = n;
}
getDepth(T->lchild,n+1,level);
getDepth(T->rchild,n+1,level);
}
}
int getBitreeDepth(BiTree T)
{
int level = 0;
int n = 1;
getDepth(T,n,&level);
return level ;
}
main()
{
BiTree T = NULL; /*最開始T指向空*/
printf("Input some characters to create a binary tree \n");
CreatBiTree(&T); /*建立二叉樹*/
printf("\nThe depth of the binary tree is %d\n",getBitreeDepth(T));
getchar() ;
getchar() ;
}
方法二
int getBitreeDepth(BiTree T){
int leftHeight, rightHeight, maxHeight;
if(T != NULL){
leftHeight = getBitreeDepth(T->lchild); // 計算左子樹的深度
rightHeight = getBitreeDepth(T->rchild); // 計算右子樹的深度
maxHeight = leftHeight > rightHeight ? leftHeight : rightHeight; // 比較左右子樹的深度
return maxHeight + 1; // 返回二叉樹的深度
else{
return 0;
}
}
二叉樹葉子結點個數
#include "string.h"
#include "stdio.h"
#include "malloc.h"
typedef struct BiTNode{
char data; /*結點的資料域*/
struct BiTNode *lchild , *rchild; /*指向左孩子和右孩子*/
} BiTNode , *BiTree;
void CreatBiTree(BiTree *T){
char c;
scanf("%c",&c);
if(c == ' ') *T = NULL;
else{
*T = (BiTNode * )malloc(sizeof(BiTNode)); /*建立根結點*/
(*T)->data = c; /*向根結點中輸入資料*/
CreatBiTree(&((*T)->lchild)); /*遞迴地建立左子樹*/
CreatBiTree(&((*T)->rchild)); /*遞迴地建立右子樹*/
}
}
void getLeavesConut (BiTree T,int *count){
if(T!=NULL && T->lchild==NULL && T->rchild==NULL){ /*訪問到葉結點*/
*count = *count + 1;
}
if(T){
getLeavesConut (T->lchild,count); /*先序遍歷T的左子樹*/
getLeavesConut (T->rchild,count); /*先序遍歷T的右子數*/
}
}
int getBiTreeLeavesCount(BiTree T) {
int count = 0; /*在主調函式中定義變數count,初始值為0*/
getLeavesConut(T, &count); /*呼叫遞迴函式getLeavesConut計算葉子結點個數*/
return count; /*返回葉子結點個數*/
}
main()
{
BiTree T = NULL; /*初始化T */
int count = 0;
printf("Input some characters to create a binary tree \n");
CreatBiTree(&T); /*建立一棵二叉樹*/
getLeavesConut (T,&count); /*計算二叉樹中葉子結點的個數 */
printf("The number of leaves of BTree are %d\n",count);
getchar();
getchar();
}
二叉排序樹
二又排序樹或者為一棵空樹,或者是具有下列性質的二又樹:
- 若它的左子樹不為空,則左子樹上的所有結點的值均小於根結點的值
- 若它的右子樹不為空,則右子樹上的所有結點的值均大於根節點的值
- 二叉排序樹的左右子樹也都是二叉排序樹

二叉排序樹的查詢
BiTree SearchBST(BiTree T, dataTYpe){
if(T == NULL)
return NULL;
if(T->data == key)
return T;
if(key < T->data)
return SearchBST(T-> lchild, key);
else
return SearchBST(T-> rchild, key);
}
最低公共祖先

分析
從整棵二又排序樹的根結點出發,
當訪間的當前結點同時大於給定的兩個結點時、沿左指前進;
當訪間的當前結點同時小於給定的兩個結點時,沿右指標前進;
當第一次訪問到介於給定的兩個結點值之間的那個結點時即是它們的最低公共祖先結點
然鵝,這個演算法並不完善,因為這個演算法適用的前提是給定的兩個結點分別位於二叉排序樹中某個結點的左右子樹上
假設給定的兩個結點分別為a和b,並且 a 是 b 的祖先,那麼結點 a 和 b 的最低公共祖先就是 a 的父結點,因為 a 的父結點一定也是 b 的祖先,同時該結點也必然是 a 和 b 的最低公共祖先。
另外,如果給定的 a 或 b 其中一個為根結點的值,那麼這種情況是不存在公共最低祖先的,因為根結點沒有祖先,所以也應把這種情況考慮進去。
#include "stdio.h"
#include "malloc.h"
#include "string.h"
typedef struct BiTNode{
int data; /*結點的資料域*/
struct BiTNode *lchild;
struct BiTNode *rchild; /*指向左孩子和右孩子*/
} BiTNode , *BiTree;
int findLowestCommonAncestor(BiTree T,int value1, int value2) {
BiTree curNode = T; /*curNode為當前訪問結點,初始化為T*/
if(T->data == value1 || T->data == value2) {
return -1; /*value1和value2有一個為根結點,因此沒有公共祖先,返回-1*/
}
while(curNode != NULL){
if (curNode->data > value1 &&
curNode->data > value2 && curNode->lchild->data != value1 &&
curNode->lchild->data != value2) {
/*當前結點的值同時大於value1和value2,且不是value1和value2的父結點*/
curNode = curNode->lchild;
} else if (curNode->data < value1 &&
curNode->data < value2 && curNode->rchild->data != value1 &&
curNode->rchild->data != value2) {
/*當前結點的值同時小於value1和value2,且不是value1和value2的父結點*/
curNode = curNode->rchild;
} else {
return curNode->data; /*找到最低公共祖先*/
}
}
}
void CreatBiTree(BiTree
