尤拉計劃問題四matlab實現
Problem4: Largest palindrome product
A palindromic number reads the same both ways. The largest palindrome made from the product of two 2-digit numbers is 9009 = 91 x 99.
Find the largest palindrome made from the product of two 3-digit numbers.
思路:
首先了解一下什麼是迴文數,就是說從左往右讀,或從右往左讀都是一樣的,比如828,1221, 75157,328823 等等,隨便舉了幾個例子,我一想覺得這樣的迴文數有很多,於是我順便寫了個程式碼測試一下,得到由兩位數相乘得到的迴文數確實很多。
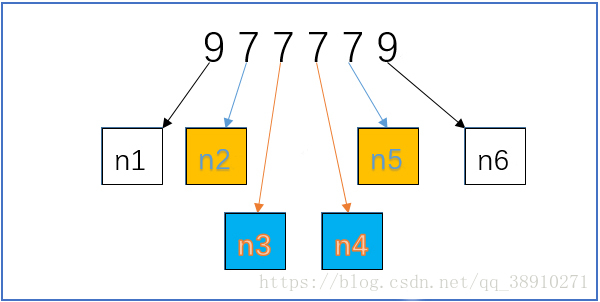
據題意由兩位數相乘所得的最大回文數是9009,並且可以因式分解為91乘以99,首先兩位數相乘的範圍是【100,9801】,發現最大回文數是接近範圍的上限的,那麼同理三位數相乘的範圍是【10000,999801】,那麼我們先大膽的猜測最大回文數應該是接近999801的,我們採用逆向思維,從上限反推回去,那麼我們得到的第一個迴文數就是最大回文數!當我們遇到問題的時候,胡適先生說過要大膽假設,小心求證。OK,我們先大膽假設一個迴文數,比如說下圖這個數,我們一分為二來說,迴文數滿足的條件為:
如果滿足上述條件,則讓該回文數除以一個變數 i,該變數從999到100迴圈,如果能被整除,則顯示出來,語言總是很蒼白,直接上程式碼,其中floor函式就是商取整.
比如 x = floor(5/4),那麼x就等於1,而不是等於1.25,mod函式就是取餘函式,比如說y=mod(10,5) 那麼y就等於0,詳細的可以參見matlab的幫助文件,要多學習去看matlab幫助文件,編寫matlab軟體的人才是最懂這個軟體的人。
clear,clc; for k =999801:-1:100000 n1 = floor(k/100000); %首位--n1 n6 = mod(k,10); %末位--n6 if n1 == n6 n2 = mod(floor((k-n6)./10000),10); %第二位--n2 n5 = floor(mod((k-n6),100)/10); %第五位--n5 if n2 == n5 n3 = floor(mod((k-n6),10000)./1000); %第三位--n3 n4 = floor(mod(mod((k-n6),10000),1000)/100);%第四位--n4 if n3 == n4 for i = 999:-1:100 if mod(k,i) == 0 n7 = fix(k/i); n8 = floor(n7/100); n9 = floor(i/100); if n8 == n9 disp(k),disp(i); break end end end end end end end
程式碼可能比較冗餘,大家有什麼好的想法可以貼出來一下,大家相互交流,共同進步!