20172313 2018-2019-1 《程式設計與資料結構》實驗二報告
阿新 • • 發佈:2018-11-10
20172313 2018-2019-1 《程式設計與資料結構》實驗一報告
課程:《程式設計與資料結構》
班級: 1723
姓名: 餘坤澎
學號:20172313
實驗教師:王志強
實驗日期:2018年9月26日
必修/選修: 必修
1.實驗內容
- 實驗一 參考教材p212,完成鏈樹LinkedBinaryTree的實現(getRight,contains,toString,preorder,postorder),用JUnit或自己編寫驅動類對自己實現的LinkedBinaryTree進行測試,提交測試程式碼執行截圖,要全屏,包含自己的學號資訊,課下把程式碼推送到程式碼託管平臺。
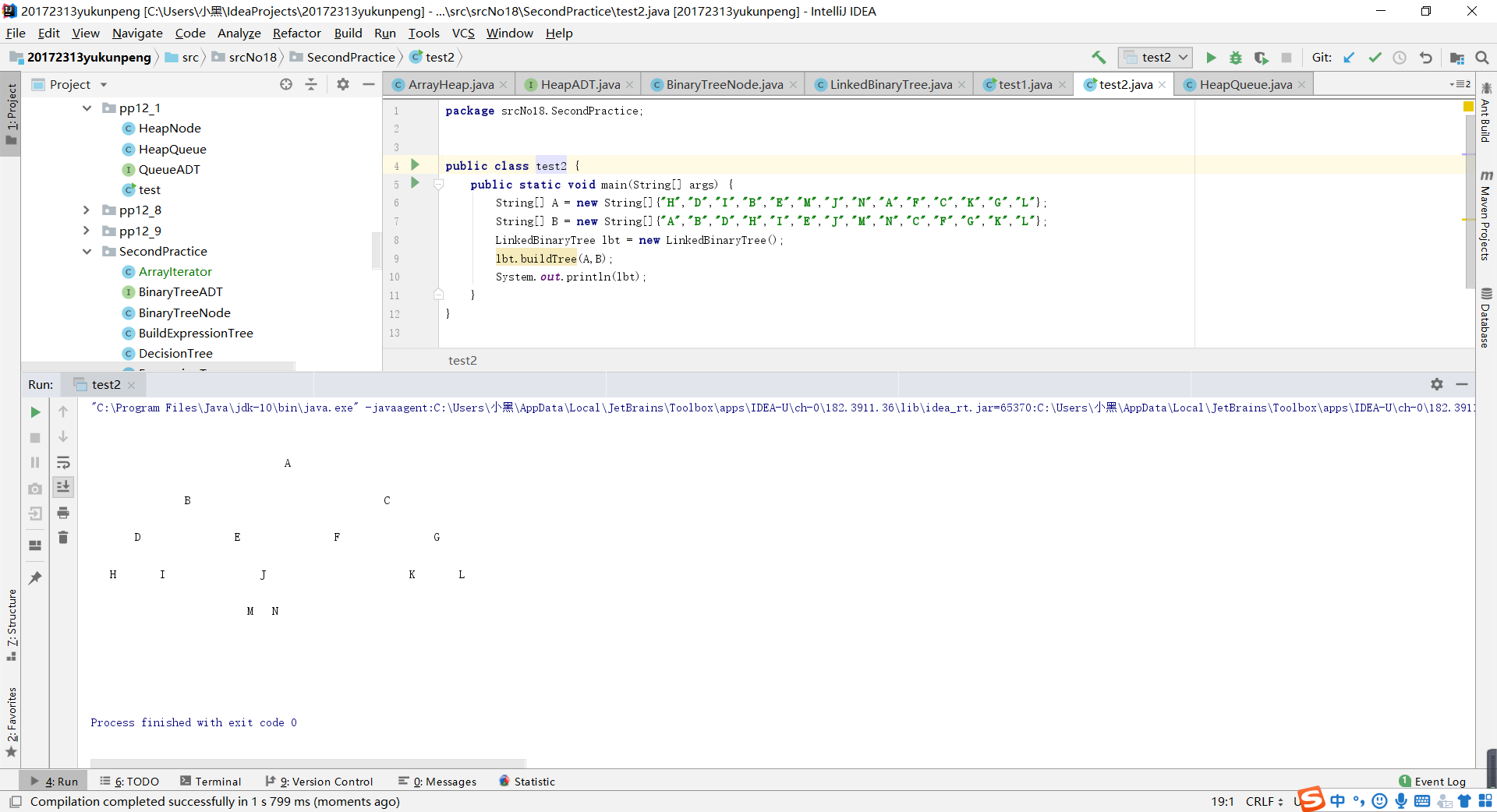
- 實驗二 基於LinkedBinaryTree,實現基於(中序,先序)序列構造唯一一棵二㕚樹的功能,比如給出中序HDIBEMJNAFCKGL和後序ABDHIEJMNCFGKL,構造出附圖中的樹,用JUnit或自己編寫驅動類對自己實現的功能進行測試,提交測試程式碼執行截圖,要全屏,包含自己的學號資訊,課下把程式碼推送到程式碼託管平臺。
- 實驗三 自己設計並實現一顆決策樹,提交測試程式碼執行截圖,要全屏,包含自己的學號資訊,課下把程式碼推送到程式碼託管平臺。
- 實驗四 輸入中綴表示式,使用樹將中綴表示式轉換為字尾表示式,並輸出字尾表示式和計算結果(如果沒有用樹,則為0分),提交測試程式碼執行截圖,要全屏,包含自己的學號資訊,課下把程式碼推送到程式碼託管平臺。
- 實驗五 完成PP11.3,提交測試程式碼執行截圖,要全屏,包含自己的學號資訊,課下把程式碼推送到程式碼託管平臺。
- 實驗六 參考http://www.cnblogs.com/rocedu/p/7483915.html對Java中的紅黑樹(TreeMap,HashMap)進行原始碼分析,並在實驗報告中體現分析結果。
2. 實驗過程及結果
實驗一
- getRight方法只需要新定義一個LinkedBinaryTree類,令它的根結點等於原樹的右子樹的結點即可。注意:首先要判斷原樹的根結點是否為空,若空,則丟擲異常。
public LinkedBinaryTree<T> getRight() { if(root == null) throw new EmptyCollectionException("Get right operation failed. The tree is empty."); LinkedBinaryTree<T> result = new LinkedBinaryTree<>(); result.root = root.getRight(); return result; }
- contains方法呼叫findNode方法即可。當findNode返回值不為空時,該方法返回true,即存在,否則不存在。
public boolean contains(T targetElement)
{
if(findNode(targetElement,root) != null)
return true;
else
return false;
}- 在這裡toString我使用的是原先學習的按照樹的形狀列印樹的方法。
public String toString() {
UnorderedListADT<BinaryTreeNode> nodes =
new ArrayUnorderedList<BinaryTreeNode>();
UnorderedListADT<Integer> levelList =
new ArrayUnorderedList<Integer>();
BinaryTreeNode current;
String result = "";
int printDepth = this.getHeight();
int possibleNodes = (int)Math.pow(2, printDepth + 1);
int countNodes = 0;
nodes.addToRear(root);
Integer currentLevel = 0;
Integer previousLevel = -1;
levelList.addToRear(currentLevel);
while (countNodes < possibleNodes)
{
countNodes = countNodes + 1;
current = nodes.removeFirst();
currentLevel = levelList.removeFirst();
if (currentLevel > previousLevel)
{
result = result + "\n\n";
previousLevel = currentLevel;
for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)
result = result + " ";
}
else
{
for (int i = 0; i < ((Math.pow(2, (printDepth - currentLevel + 1)) - 1)) ; i++)
{
result = result + " ";
}
}
if (current != null)
{
result = result + (current.getElement()).toString();
nodes.addToRear(current.getLeft());
levelList.addToRear(currentLevel + 1);
nodes.addToRear(current.getRight());
levelList.addToRear(currentLevel + 1);
}
else {
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
result = result + " ";
}
}
return result;
}
- preorder,postorder方法參考書上inorder方法即可。(在這裡只列舉preorder方法的程式碼)
public Iterator<T> iteratorPreOrder()
{
ArrayUnorderedList<T> tempList = new ArrayUnorderedList<T>();
preOrder(root, tempList);
return new TreeIterator(tempList.iterator());
}
protected void preOrder(BinaryTreeNode<T> node,
ArrayUnorderedList<T> tempList)
{
if (node != null)
{
tempList.addToRear(node.getElement());
preOrder(node.getLeft(), tempList);
preOrder(node.getRight(), tempList);
}
}- 所有方法實現之後,編寫驅動類對LinkedBinaryTree進行測試。

實驗二
- 實驗一比較容易,所有的程式碼基本上在以前都實現過,稍加參考就能完成。實驗二就比較難了,要使用中序序列和前序序列構造二叉樹。設計思路如下:
- ①我們要確定根節點的位置,先序遍歷的第一個結點就是該二叉樹的根。
- ② 確定根的子樹,有中序遍歷可知,我們在中序遍歷中找到根結點的位置,左邊是它的左孩子,右邊是它的右孩子,如果根結點左邊或右邊為空,那麼在該方向上子樹為空,如果根結點左邊和右邊都為空,那麼該結點是葉子結點。
- ③對二叉樹的左、右子樹分別進行步驟①②,直到求出二叉樹的結構為止。
- 該實驗的主要難度在於如何使用遞迴不斷對左右子樹重複進行①②步驟,可根據傳入的序列的陣列的索引值進行分割,在中序序列中但凡比根元素索引值小的即為根元素的左結點,大的即為根元素的右結點。按照中序序列分成的兩部分元素又可以把前序序列分成兩部分,接下來用遞迴,把新得到的序列陣列作為引數,直到形成二叉樹的結構。
public void buildTree(T[] inorder, T[] postorder) {
BinaryTreeNode temp=makeTree(inorder, 0, inorder.length, postorder, 0, postorder.length);
root = temp;
}
public BinaryTreeNode<T> makeTree(T[] inorder,int startIn,int lenIn,T[] postorder,int startPos,int lenPos){
if(lenIn<1){
return null;
}
BinaryTreeNode root;
T rootelement=postorder[startPos];//postorder中的第一個元素就是當前處理的資料段的根節點
root=new BinaryTreeNode(rootelement);
int temp;
boolean isFound=false;
for(temp=0;temp<lenIn;temp++){
if(inorder[startIn+temp]==rootelement){
isFound=true;//此時找到結點
break;
}
}
if(!isFound)//如果不存在相等的情況就跳出該函式
return root;
root.setLeft(makeTree(inorder, startIn, temp, postorder, startPos+1, temp));
root.setRight(makeTree(inorder, startIn+temp+1, lenIn-temp-1, postorder, startPos+temp+1, lenPos-temp-1));
return root;
}
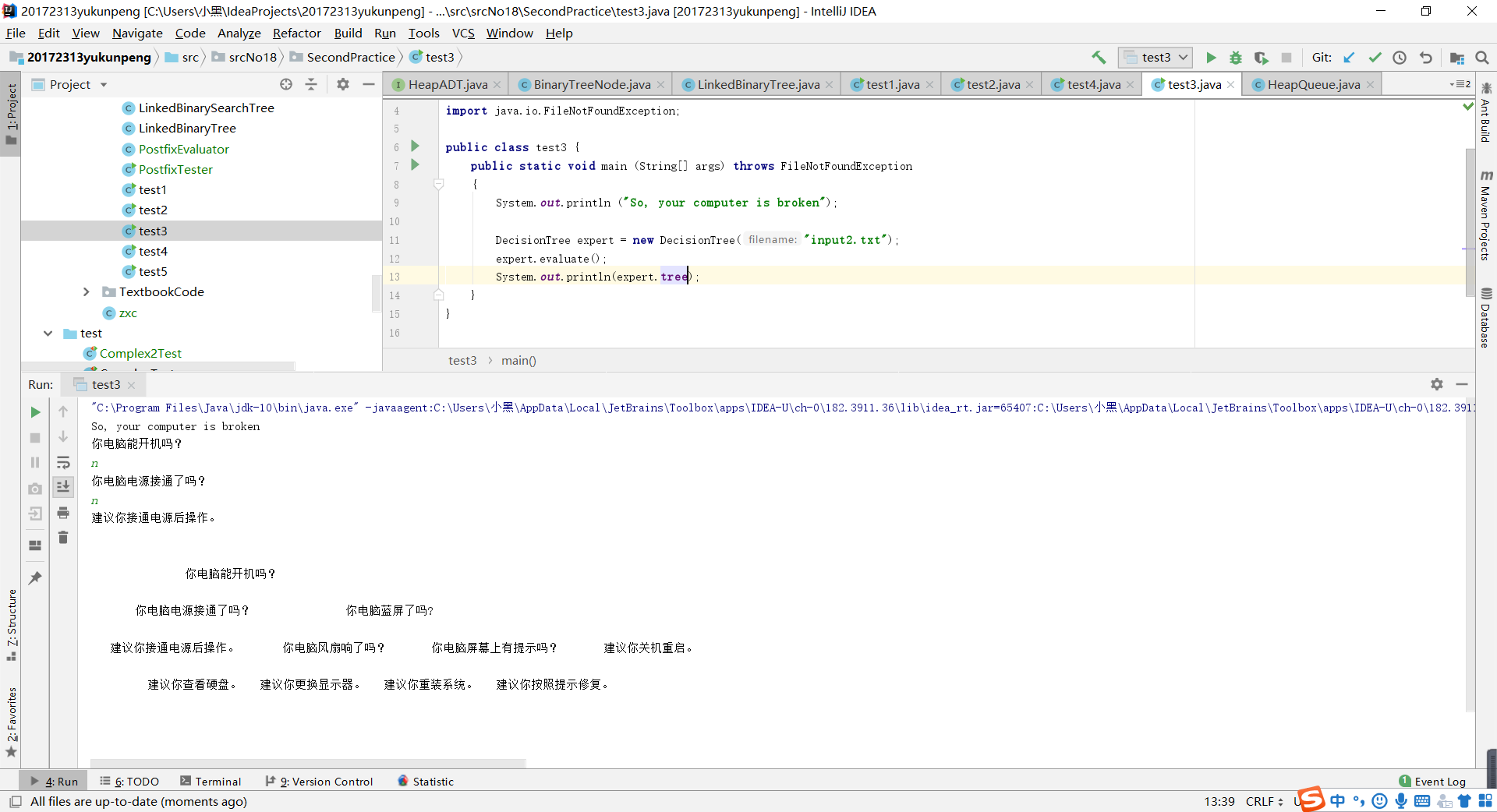
實驗三
- 實驗三可以說是最簡單的了,有了書上的示例進行參考,對檔案進行修改即可,在這裡不再過多贅述。
實驗四
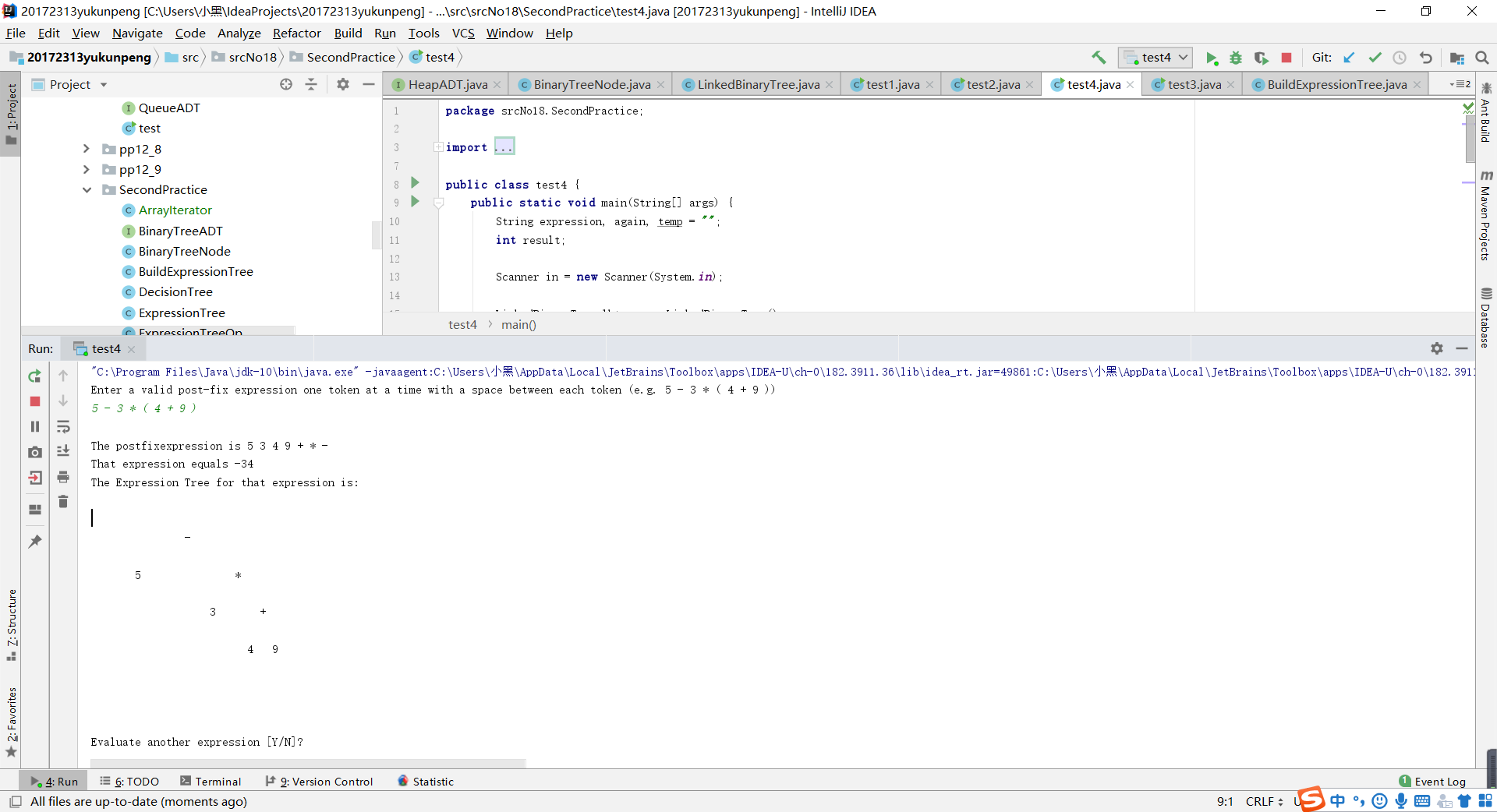
- 這個實驗是本次實驗中最有難度的一個,雖然原先學習過中綴表示式轉字尾表示式求值的問題,但使用樹來進行操作還是第一次。使用字尾表示式進行求值課堂上學習過,書上也有示例程式碼。這裡只列舉使用樹把中綴表示式變為字尾表示式。設計思路如下:
- 定義兩個列表分別用來操作符和“子樹“,注意:這裡的操作符列表裡只存“+”“-”,至於為什麼將在下面進行分析。首先把中綴表示式用StringTokenizer方法進行分開,從前到後依次遍歷,如果是括號,就把括號裡面的內容作為一個新的表示式傳入該方法,把返回的結點作為一棵新樹的根存進numList。如果遍歷到數字,作為一棵新樹的element存入numList,如果遍歷到“+”“-”,直接存入operLIst中。如果遇到“乘或除”,如果“乘或除”的往後遍歷到的是括號,則先把括號裡的內容作為一個新的表示式傳入該方法,把返回的結點作為“乘號”的右子樹的根結點,然後從numList取出最後一個元素作為“乘號”的左子樹的根結點。如果“乘或除”的往後遍歷到的是數字,則直接作為“乘號”的右子樹的根結點,然後從numList取出最後一個元素作為“乘號”的左子樹的根結點。
- 這裡的核心思想就是一旦遇到括號就把括號裡的內容作為引數傳入該方法,由於括號運算的優先順序,可以把得到的該結點傳入numList,在形成二叉樹的過程中直接取出。一旦遇到“乘或除”就從numList的末尾取出一位元素作為它的左子樹,“乘或除”的下一位元素作為它的右子樹,然後把這個子樹存入numList,這樣在保證了運算優先順序的同時,也使得形成二叉樹的時候順序不會被打亂,這就是為什麼操作符列表裡只存“+”“-”操作符列表裡只存“+”“-”,因為“乘或除”作為子樹的根結點都存入到了numList。一直到遍歷完成,這時候我們知道,最先進入numList的運算優先順序最高,所以從索引為0處開始取元素,把它們組裝成一棵二叉樹即可。
public BinaryTreeNode buildTree(String str) { ArrayList<String> operList = new ArrayList<>(); ArrayList<LinkedBinaryTree> numList = new ArrayList<>(); StringTokenizer st = new StringTokenizer(str); String token; while (st.hasMoreTokens()) { token = st.nextToken(); if (token.equals("(")) { String str1 = ""; while (true) { token = st.nextToken(); if (!token.equals(")")) str1 += token + " "; else break; } LinkedBinaryTree temp = new LinkedBinaryTree(); temp.root = buildTree(str1); numList.add(temp); token = st.nextToken(); } if (token.equals("+") || token.equals("-")) { operList.add(token); } else if (token.equals("*") || token.equals("/")) { LinkedBinaryTree left = numList.remove(numList.size() - 1); String A = token; token = st.nextToken(); if (!token.equals("(")) { LinkedBinaryTree right = new LinkedBinaryTree(token); LinkedBinaryTree node = new LinkedBinaryTree(A, left, right); numList.add(node); } else { String str1 = ""; while (true) { token = st.nextToken(); if (!token.equals(")")) str1 += token + " "; else break; } LinkedBinaryTree temp2 = new LinkedBinaryTree(); temp2.root = buildTree(str1); LinkedBinaryTree node1 = new LinkedBinaryTree(A, left, temp2); numList.add(node1); } } else numList.add(new LinkedBinaryTree(token)); } while (operList.size() > 0) { LinkedBinaryTree left = numList.remove(0); LinkedBinaryTree right = numList.remove(0); String oper = operList.remove(0); LinkedBinaryTree node2 = new LinkedBinaryTree(oper, left, right); numList.add(0, node2); } node = (numList.get(0)).root; return node; }
實驗五
- 實驗五相較於實驗四來說又簡單了一些,由於二叉查詢樹的最小元素始終位於整棵樹左下角最後一個左子樹的第一個位置,最大元素始終位於整棵樹右下角最後一個右子樹的最後一個位置。從根結點進行遍歷即可。注意:這裡要判斷樹為空和結點的左右子樹是否存在。
public T removeMax() throws EmptyCollectionException
{
T result = null;
if (isEmpty())
throw new EmptyCollectionException("LinkedBinarySearchTree");
else
{
if (root.right == null)
{
result = root.element;
root = root.left;
}
else
{
BinaryTreeNode<T> parent = root;
BinaryTreeNode<T> current = root.right;
while (current.right != null)
{
parent = current;
current = current.right;
}
result = current.element;
parent.right = current.left;
}
modCount--;
}
return result;
}
public T findMin() throws EmptyCollectionException
{
if(isEmpty())
System.out.println("BinarySearchTree is empty!");
return findMin(root).getElement();
}
private BinaryTreeNode<T> findMin(BinaryTreeNode<T> p) {
if (p==null)//結束條件
return null;
else if (p.left==null)//如果沒有左結點,那麼t就是最小的
return p;
return findMin(p.left);
}
public T findMax() throws EmptyCollectionException
{
if(isEmpty())
System.out.println("BinarySearchTree is empty!");
return findMax(root).getElement();
}
private BinaryTreeNode<T> findMax(BinaryTreeNode<T> p){
if (p==null)//結束條件
return null;
else if (p.right==null)
return p;
return findMax(p.right);
}實驗六
- 紅黑樹(Red Black Tree) 是一種自平衡二叉查詢樹,是在電腦科學中用到的一種資料結構,典型的用途是實現關聯陣列。首先,我們先來看看它的性質
- 樹中的每一個結點都儲存著一種顏色(紅色或黑色,通常使用一個布林值來實現,值false等價於紅色)。
- 根結點為黑色。
- 每個葉子結點(null)是黑色。(**注意:這裡的葉子結點,是指為空(null)的葉子結點!)
- 從樹根到樹葉的每條路徑都包含有同樣數目的黑色結點。
- 如果一個結點的顏色為紅色,那麼它的子結點必定是黑色。
- 紅黑樹示意圖:

- TreeMap概述:TreeMap是基於紅黑樹實現的。由於TreeMap實現了java.util.sortMap介面,集合中的對映關係是具有一定順序的,該對映根據其鍵的自然順序進行排序或者根據建立對映時提供的Comparator進行排序,具體取決於使用的構造方法。另外TreeMap中不允許鍵物件是null。
- TreeMap類:
public class TreeMap<K,V> extends AbstractMap<K,V> implements NavigableMap<K,V>, Cloneable, java.io.SerializableTreeMap 是一個有序的key-value集合,它是通過紅黑樹實現的。
TreeMap 繼承於AbstractMap,所以它是一個Map,即一個key-value集合。
TreeMap 實現了NavigableMap介面,意味著它支援一系列的導航方法。比如返回有序的key集合。
TreeMap 實現了Cloneable介面,意味著它能被克隆。
TreeMap 實現了java.io.Serializable介面,意味著它支援序列化。 - TreeMap常用方法:
- TreeMap的建構函式
//使用預設建構函式構造TreeMap時,使用java的預設的比較器比較Key的大小,從而對TreeMap進行排序。 public TreeMap() { comparator = null; } //帶比較器的建構函式 public TreeMap(Comparator<? super K> comparator) { this.comparator = comparator; } //帶Map的建構函式,Map會成為TreeMap的子集 ublic TreeMap(Map<? extends K, ? extends V> m) { comparator = null; putAll(m); } //該建構函式會呼叫putAll()將m中的所有元素新增到TreeMap中。從中,我們可以看出putAll()就是將m中的key-value逐個的新增到TreeMap中。putAll()原始碼如下: public void putAll(Map<? extends K, ? extends V> m) { for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) put(e.getKey(), e.getValue()); } //帶SortedMap的建構函式,SortedMap會成為TreeMap的子集,該建構函式不同於上一個建構函式,在上一個建構函式中傳入的引數是Map,Map不是有序的,所以要逐個新增。而該建構函式的引數是SortedMap是一個有序的Map,我們通過buildFromSorted()來建立對應的Map。 public TreeMap(SortedMap<K, ? extends V> m) { comparator = m.comparator(); try { buildFromSorted(m.size(), m.entrySet().iterator(), null, null); } catch (java.io.IOException cannotHappen) { } catch (ClassNotFoundException cannotHappen) { } }- V put(K key,V value):將鍵值對(key,value)新增到TreeMap中
public V put(K key, V value) {//插入或設定元素,返回原始value值(如果插入返回null) Entry<K,V> t = root; if (t == null) {//根元素為空時直接建立根元素 root = new Entry<K,V>(key, value, null); size = 1; modCount++; return null; } int cmp; Entry<K,V> parent; // split comparator and comparable paths Comparator<? super K> cpr = comparator; if (cpr != null) {//存在比較器 do {//迴圈查詢父元素 parent = t;//設定父元素 cmp = cpr.compare(key, t.key); if (cmp < 0) t = t.left;//繼續查詢左邊元素 else if (cmp > 0) t = t.right;//繼續查詢右邊元素 else return t.setValue(value);//相等直接進行value設定 } while (t != null); } else {//不存在比較器,按compareTo方法查詢 if (key == null) throw new NullPointerException(); Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; cmp = k.compareTo(t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } Entry<K,V> e = new Entry<K,V>(key, value, parent); if (cmp < 0) parent.left = e; else parent.right = e; fixAfterInsertion(e); size++; modCount++; return null; } private void fixAfterInsertion(Entry<K,V> x) {//插入資料後的樹形變化處理 x.color = RED;//插入元素預設顏色為紅色 while (x != null && x != root && x.parent.color == RED) {//當父節點的顏色為紅色時,需要進行變化 if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {//如果父元素為其父的左節點 Entry<K,V> y = rightOf(parentOf(parentOf(x)));//取右節點(叔節點) if (colorOf(y) == RED) {//顏色為紅 setColor(parentOf(x), BLACK);//父節點設定為黑色 setColor(y, BLACK);//右節點設定為黑色 setColor(parentOf(parentOf(x)), RED);//父元素的父元素設定為紅色 x = parentOf(parentOf(x));//x設定為父元素的父元素,繼續進行判定 } else {//叔節點不可能為黑色,故下面為無叔節點情況,必然需要進行旋轉 if (x == rightOf(parentOf(x))) {//如果當前元素為其父的右節點 x = parentOf(x);//x設定為父元素,繼續進行判定 rotateLeft(x);//進行左旋操作 } setColor(parentOf(x), BLACK);//父節點設定為黑色 setColor(parentOf(parentOf(x)), RED);//父元素的父元素設定為紅色 rotateRight(parentOf(parentOf(x)));//進行右旋操作 } } else {//父元素為其父的右節點 Entry<K,V> y = leftOf(parentOf(parentOf(x)));//取左節點(叔節點) if (colorOf(y) == RED) {//顏色為紅 setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x));//x設定為父元素的父元素,繼續進行判定 } else {//叔節點不可能為黑色,故下面為無叔節點情況,必然需要進行旋轉 if (x == leftOf(parentOf(x))) {//如果當前元素為其父的左節點 x = parentOf(x);//x設定為父元素,繼續進行判定 rotateRight(x);//進行右旋操作 } setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateLeft(parentOf(parentOf(x)));//進行左旋操作 } } } root.color = BLACK;//根節點設定為黑色 }- 按照key值進行查詢
final Entry<K,V> getEntry(Object key) {//根據key值查詢元素方法;final方法不允許被子類重寫
// Offload comparator-based version for sake of performance
if (comparator != null)//存在比較器,按比較器進行比較查詢
return getEntryUsingComparator(key);
if (key == null)//key值為null拋空指標異常
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {//從root開始迴圈查詢,一直到葉子節點
int cmp = k.compareTo(p.key);//採用key的compareTo方法進行比較
if (cmp < 0)//小於繼續查詢左邊
p = p.left;
else if (cmp > 0)//大於繼續查詢右邊
p = p.right;
else
return p;//等於返回當前元素
}
return null;
}- 刪除操作
blic V remove(Object key) {
Entry<K,V> p = getEntry(key);//先找到需要刪除的元素
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
if (p.left != null && p.right != null) {//如果有兩個孩子
Entry<K,V> s = successor (p);//查詢下一元素
p.key = s.key;
p.value = s.value;//p的資料替換為該元素資料
p = s;//將p指向該元素,作為原始元素(被刪除元素)
} // p has 2 children
// Start fixup at replacement node, if it exists.
Entry<K,V> replacement = (p.left != null ? p.left : p.right);//將替換元素設定為左元素(沒有則為右元素)
if (replacement != null) {//替換元素不為空
// Link replacement to parent
replacement.parent = p.parent;//將替換元素與原始元素的父親連線起來
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
p.left = p.right = p.parent = null;//原始元素連線清空
// Fix replacement
if (p.color == BLACK)//刪除元素為黑色,需要進行刪除後樹形變化操作
fixAfterDeletion(replacement);
} else if (p.parent == null) { // return if we are the only node.
root = null;//根節點的刪除
} else { // No children. Use self as phantom replacement and unlink.
if (p.color == BLACK)
fixAfterDeletion(p);
//沒有孩子時,使用自己作為替換節點,先樹形變化再進行連線清空操作
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}
private void fixAfterDeletion(Entry<K,V> x) {//刪除資料後的樹形變化處理
while (x != root && colorOf(x) == BLACK) {//當前節點為黑(替換元素不可能為黑,只有刪除自身的情況)
if (x == leftOf(parentOf(x))) {//左節點
Entry<K,V> sib = rightOf(parentOf(x));//取父親的右節點(兄節點)
if (colorOf(sib) == RED) {//顏色為紅
setColor(sib, BLACK);
setColor(parentOf(x), RED);//著色
rotateLeft(parentOf(x));//按父左旋
sib = rightOf(parentOf(x));//指向左旋後的父親的右節點(為黑)
}
//顏色為黑
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {//兩個孩子均為黑(實際只可能為無孩子情況)
setColor(sib, RED);//著色
x = parentOf(x);//x指向父節點繼續判斷
} else {
if (colorOf(rightOf(sib)) == BLACK) {//右節點為黑(實際只可能為無右孩子)
setColor(leftOf(sib), BLACK);
setColor(sib, RED);//著色
rotateRight(sib);//按兄右旋
sib = rightOf(parentOf(x));//指向右旋後的父親的右節點
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);//著色
rotateLeft(parentOf(x));//按父左旋
x = root;//結束迴圈
}
} else { // symmetric//右節點
Entry<K,V> sib = leftOf(parentOf(x));//取父親的左節點(兄節點)
if (colorOf(sib) == RED) {//顏色為紅
setColor(sib, BLACK);
setColor(parentOf(x), RED);//著色
rotateRight(parentOf(x));//按父右旋
sib = leftOf(parentOf(x));//指向右旋後的父親的左節點(為黑或空)
}
//顏色為黑
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {//兩個孩子均為黑
setColor(sib, RED);//著色
x = parentOf(x);//x指向父節點繼續判斷
} else {
if (colorOf(leftOf(sib)) == BLACK) {//左節點為黑
setColor(rightOf(sib), BLACK);
setColor(sib, RED);//著色
rotateLeft(sib);//按兄左旋
sib = leftOf(parentOf(x));//指向左旋後的父親的左節點
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);//著色
rotateRight(parentOf(x));//按父右旋
x = root;//結束迴圈
}
}
}
setColor(x, BLACK);//將x置為黑色
}- 紅黑樹具體的新增或刪除示意圖可參照往期部落格
- 關於 firstEntry() 和 getFirstEntry()都是用於獲取第一個結點,那麼兩者到底有什麼區別呢?
- firstEntry() 是對外介面; getFirstEntry() 是內部介面。而且,firstEntry() 是通過 getFirstEntry() 來實現的。那為什麼外界不能直接呼叫 getFirstEntry(),而需要多此一舉的呼叫 firstEntry() 呢?這麼做的目的是:防止使用者修改返回的Entry。getFirstEntry()返回的Entry是可以被修改的,但是經過firstEntry()返回的Entry不能被修改,只可以讀取Entry的key值和value值。
- HashMap類
- Java最基本的資料結構有陣列和連結串列。陣列的特點是空間連續(大小固定)、定址迅速,但是插入和刪除時需要移動元素,所以查詢快,增加刪除慢。連結串列恰好相反,可動態增加或減少空間以適應新增和刪除元素,但查詢時只能順著一個個節點查詢,所以增加刪除快,查詢慢。有沒有一種結構綜合了陣列和連結串列的優點呢?當然有,那就是雜湊表(雖說是綜合優點,但實際上查詢肯定沒有陣列快,插入刪除沒有連結串列快,一種折中的方式吧)。一般採用拉鍊法實現雜湊表。
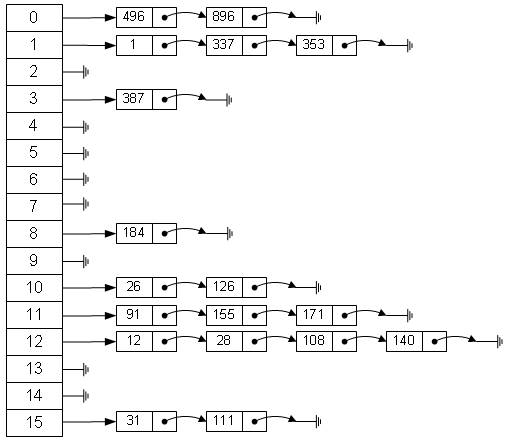
- Java最基本的資料結構有陣列和連結串列。陣列的特點是空間連續(大小固定)、定址迅速,但是插入和刪除時需要移動元素,所以查詢快,增加刪除慢。連結串列恰好相反,可動態增加或減少空間以適應新增和刪除元素,但查詢時只能順著一個個節點查詢,所以增加刪除快,查詢慢。有沒有一種結構綜合了陣列和連結串列的優點呢?當然有,那就是雜湊表(雖說是綜合優點,但實際上查詢肯定沒有陣列快,插入刪除沒有連結串列快,一種折中的方式吧)。一般採用拉鍊法實現雜湊表。
- HashMap常用方法:
- put()操作:在使用的時候,我們一定會想到如果兩個key通過hash%Entry[].length得到的index相同,會不會有覆蓋的危險?為了解決這個問題,HashMap裡面用到鏈式資料結構的一個概念。上面我們提到過Entry類裡面有一個next屬性,作用是指向下一個Entry。打個比方, 第一個鍵值對A進來,通過計算其key的hash得到的index=0,記做:Entry[0] = A。一會後又進來一個鍵值對B,通過計算其index也等於0,現在怎麼辦?HashMap會這樣做:B.next = A,Entry[0] = B,如果又進來C,index也等於0,那麼C.next = B,Entry[0] = C;這樣我們發現index=0的地方其實存取了A,B,C三個鍵值對,他們通過next這個屬性連結在一起。所以疑問不用擔心。也就是說陣列中儲存的是最後插入的元素。
public V put(K key, V value) { //如果table陣列為空陣列{},進行陣列填充(為table分配實際記憶體空間),入參為threshold,此時threshold為initialCapacity 預設是1<<4(=16) if (table == EMPTY_TABLE) { inflateTable(threshold);//分配陣列空間 } //如果key為null,儲存位置為table[0]或table[0]的衝突鏈上 if (key == null) return putForNullKey(value); int hash = hash(key);//對key的hashcode進一步計算,確保雜湊均勻 int i = indexFor(hash, table.length);//獲取在table中的實際位置 for (Entry<K,V> e = table[i]; e != null; e = e.next) { //如果該對應資料已存在,執行覆蓋操作。用新value替換舊value,並返回舊value Object k; if (e.hash == hash && ((k = e.key) == key || key.equals(k))) { V oldValue = e.value; e.value = value; e.recordAccess(this);//呼叫value的回撥函式,其實這個函式也為空實現 return oldValue; } } modCount++;//保證併發訪問時,若HashMap內部結構發生變化,快速響應失敗 addEntry(hash, key, value, i);//新增一個entry return null; }- inflateTable的原始碼如下:
private void inflateTable(int toSize) { int capacity = roundUpToPowerOf2(toSize);//capacity一定是2的次冪 threshold = (int) Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1);//此處為threshold賦值,取capacity*loadFactor和MAXIMUM_CAPACITY+1的最小值,capaticy一定不會超過MAXIMUM_CAPACITY,除非loadFactor大於1 table = new Entry[capacity];//分配空間 initHashSeedAsNeeded(capacity);//選擇合適的Hash因子 }- inflateTable這個方法用於為主幹陣列table在記憶體中分配儲存空間,通過roundUpToPowerOf2(toSize)可以確保capacity為大於或等於toSize的最接近toSize的二次冪,roundUpToPowerOf2中的這段處理使得陣列長度一定為2的次冪,Integer.highestOneBit是用來獲取最左邊的bit(其他bit位為0)所代表的數值。在對陣列進行空間分配後,會根據hash函式計算雜湊值。通過hash函式得到雜湊值後,再通過indexFor進一步處理來獲取實際的儲存位置。通過以上分析,我們看到,要得到一個元素的儲存位置,需要如下幾步:
- ①獲取該元素的key值
- ②通過hash方法得到key的雜湊值,這其中需要用到key的hashcode值。
- ③通過indexFor計算得到儲存的下標位置。
- 最後,得到儲存的下標位置後,我們就可以將元素放入HashMap中,具體通過addEntry實現:
void addEntry(int hash, K key, V value, int bucketIndex) { if ((size >= threshold) && (null != table[bucketIndex])) { resize(2 * table.length);//當size超過臨界閾值threshold,並且即將發生雜湊衝突時進行擴容,新容量為舊容量的2倍 hash = (null != key) ? hash(key) : 0; bucketIndex = indexFor(hash, table.length);//擴容後重新計算插入的位置下標 } //把元素放入HashMap的桶的對應位置 createEntry(hash, key, value, bucketIndex); } //建立元素 void createEntry(int hash, K key, V value, int bucketIndex) { Entry<K,V> e = table[bucketIndex]; //獲取待插入位置元素 table[bucketIndex] = new Entry<>(hash, key, value, e);//這裡執行連結操作,使得新插入的元素指向原有元素。 //這保證了新插入的元素總是在連結串列的頭 size++;//元素個數+1 }3. 實驗過程中遇到的問題和解決過程
- 問題1:在做第二個實驗的時候,遞迴完成後列印的二叉樹個預期的不一樣。
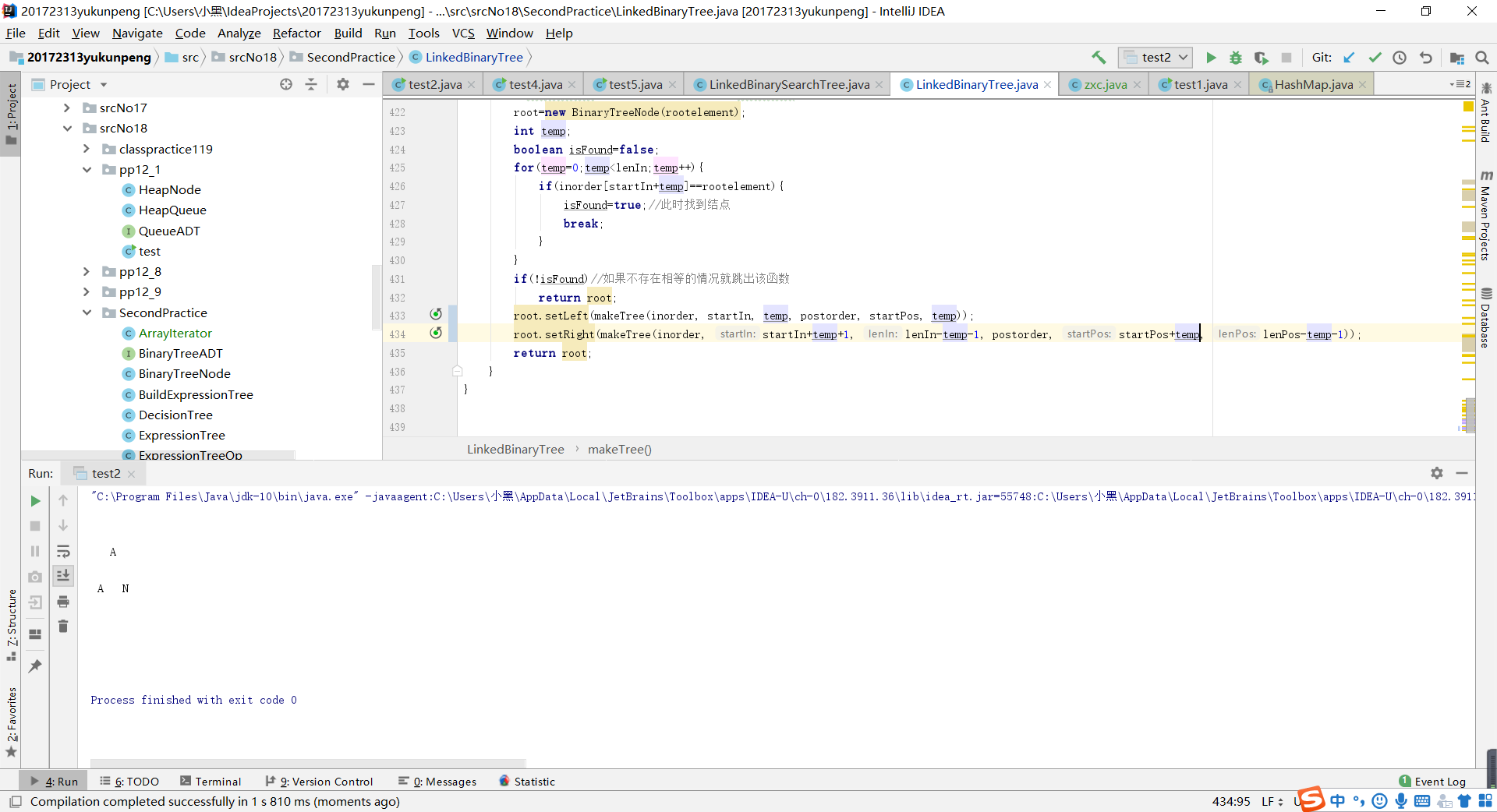
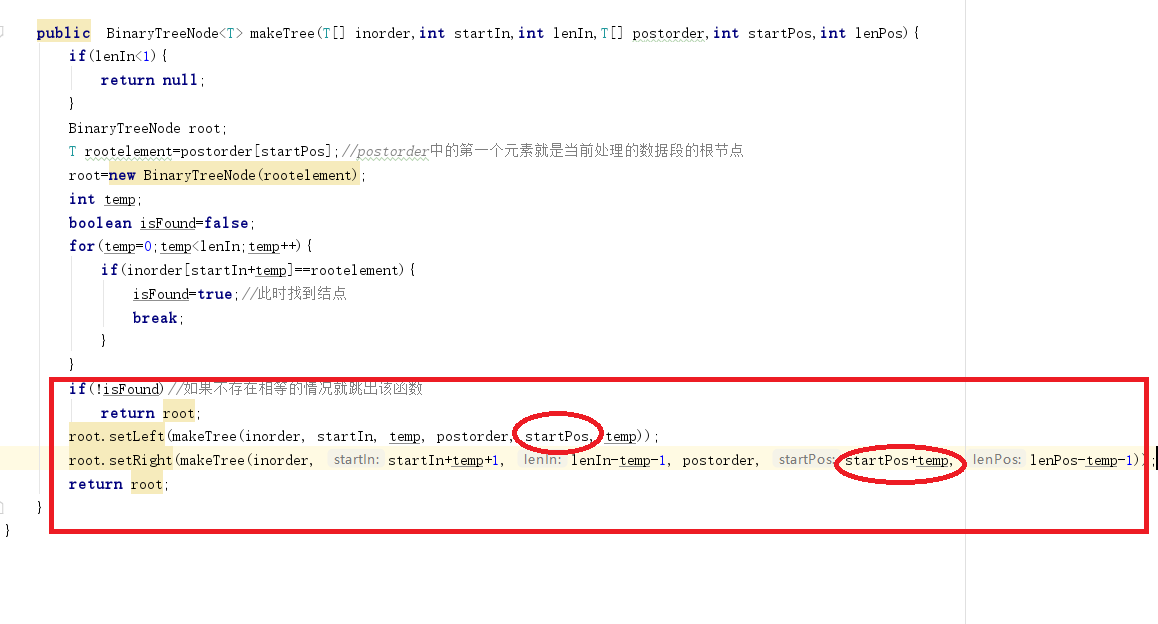
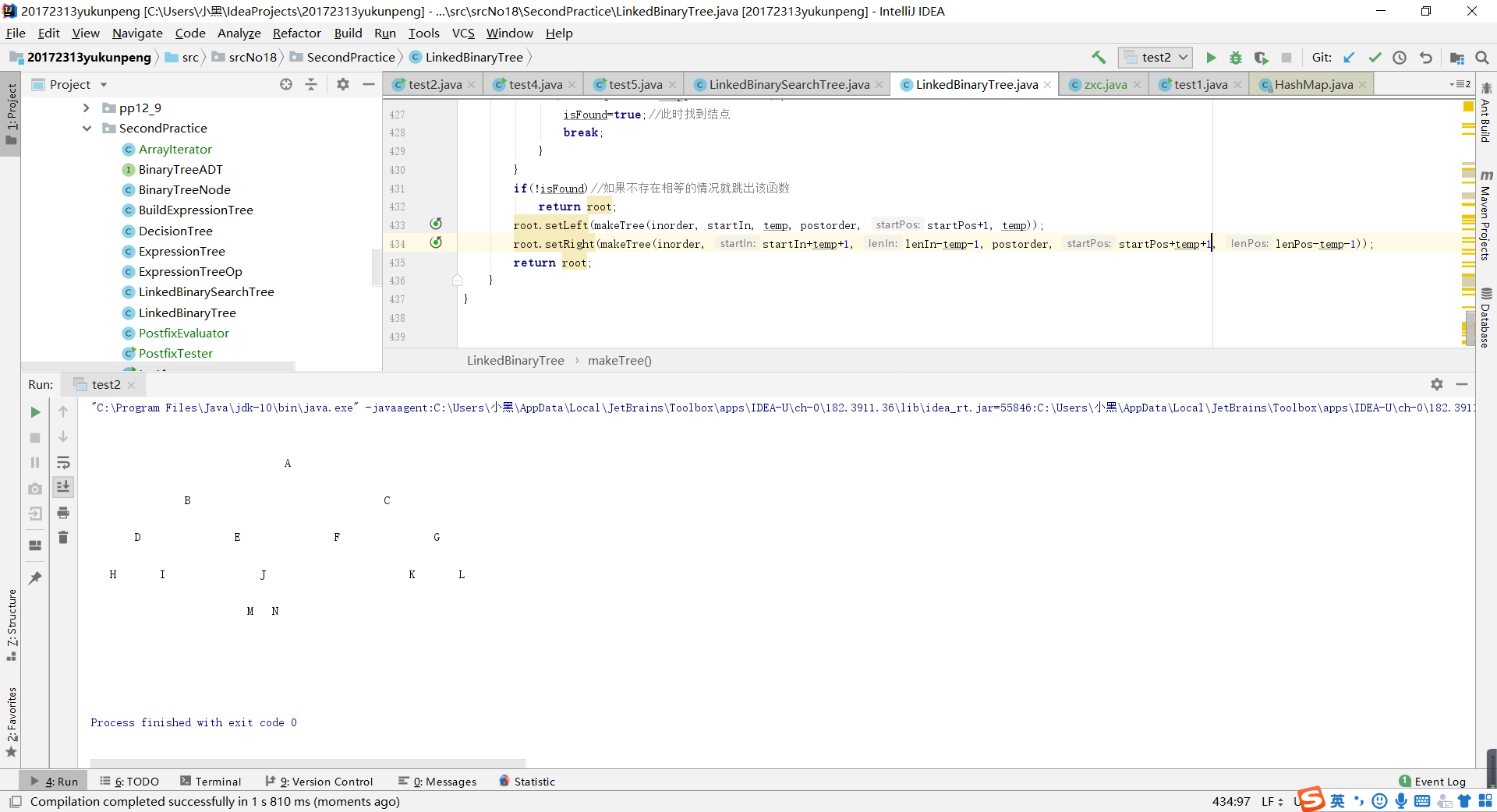
- 問題1解決方案:我先是檢查了一遍迴圈,利用迴圈在中序序列中找到根節點,我debug了一遍,沒有在迴圈這裡發現錯誤。那就是遞迴存在問題,我重新捋了一遍自己的思路,根據傳入的序列的陣列的索引值進行分割,在中序序列中但凡比根元素索引值小的即為根元素的左結點,大的即為根元素的右結點。按照中序序列分成的兩部分元素又可以把前序序列分成兩部分,接下來用遞迴,把新得到的序列陣列作為引數,直到形成二叉樹的結構。我又仔細檢查了一下自己的程式碼,發現了問題所在:因為前序序列的第一個是根元素,所以在進行遞迴傳入引數時startpos變數需要加1,加上後,問題就解決了。
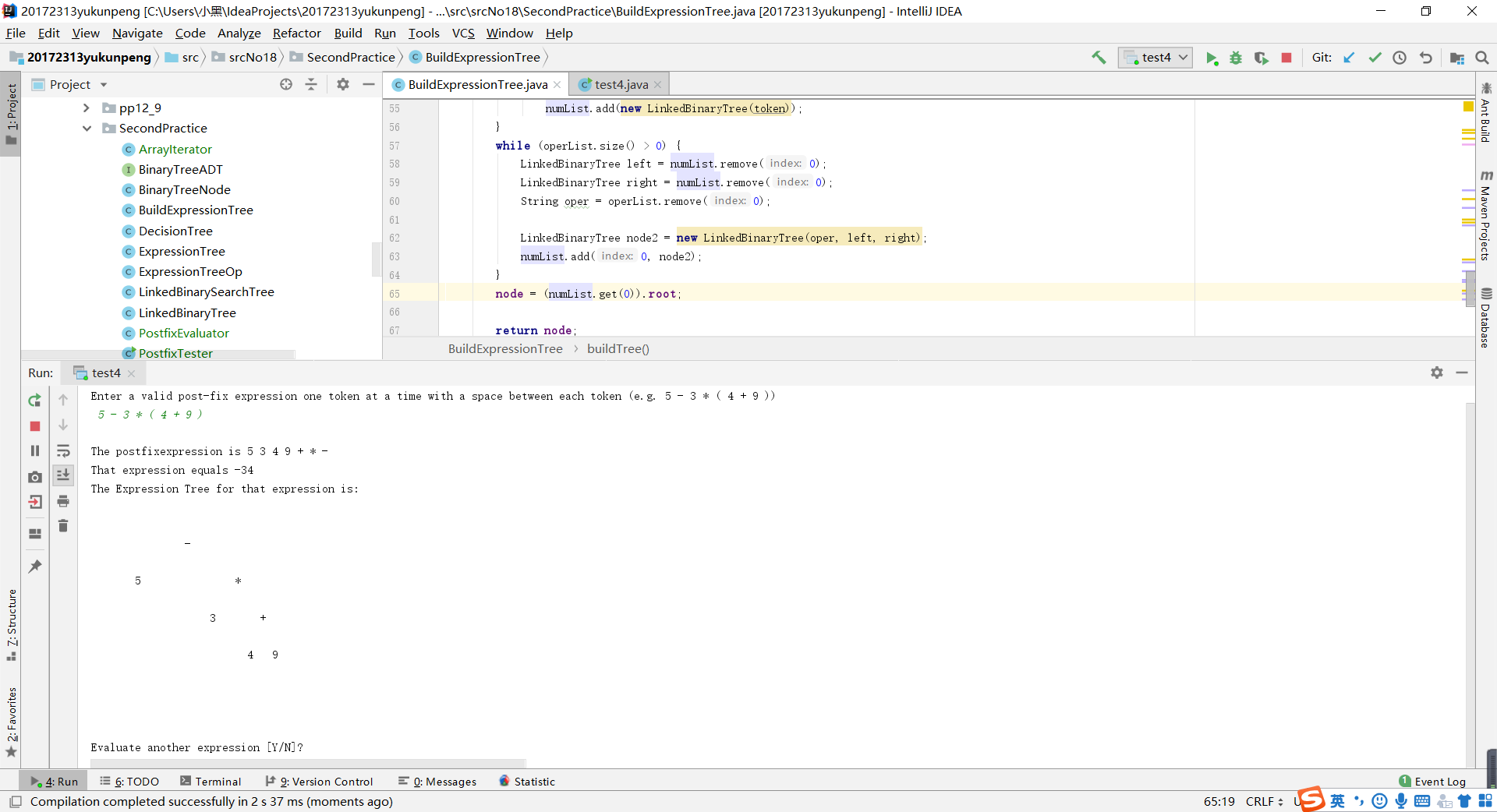
- 問題2:在做第四個實驗的時候,始終不能正確的把中綴表示式轉換為字尾表示式。
- 問題2解決方案:我先對迴圈體進行debug,由於程式碼中的判斷條件和迴圈條件過多,所以的debug的效果並不理想。我仔細檢查了一下生成的字尾表示式,發現排列的順序是相反的,這就說明從numList彈出的時候順序是不對的。我又仔細想了一下,先進入numList的優先順序是最高的,構造二叉樹的時候優先順序高的成為左子樹。所以numList是從前往後遍歷的,這樣一來,我就找到了我的問題所在。我誤在numList彈出元素的時候把索引值設定成了size()-1,改成0問題就得以解決了。

其他
這次實驗的難度分佈的比較不均勻,大體上來說就是簡單的很簡單,難的非常難,在一些小地方也浪費了很多時間,導致沒有在預想的時間內完成實驗,希望自己能在以後的學習生活中繼續努力,不斷進步!
