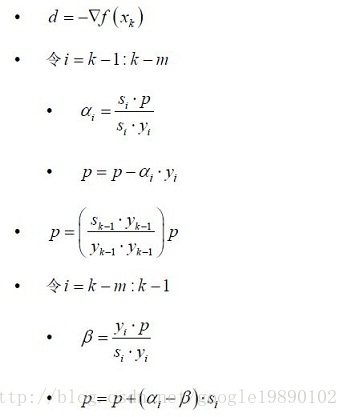2. 程式人生 > >機器學習演算法實現解析——liblbfgs之L-BFGS演算法

機器學習演算法實現解析——liblbfgs之L-BFGS演算法

阿新 • • 發佈：2018-11-11

在博文“優化演算法——擬牛頓法之L-BFGS演算法”中，已經對L-BFGS的演算法原理做了詳細的介紹，本文主要就開原始碼liblbfgs重新回顧L-BFGS的演算法原理以及具體的實現過程，在L-BFGS演算法中包含了處理L1正則的OWL-QN演算法，對於OWL-QN演算法的詳細原理，可以參見博文“優化演算法——OWL-QN”。

1、liblbfgs簡介

liblbfgs是L-BFGS演算法的C語言實現，用於求解非線性優化問題。

liblbfgs的主頁：http://www.chokkan.org/software/liblbfgs/

下載連結（見上面的主頁連結）：

https://github.com/downloads/chokkan/liblbfgs/liblbfgs-1.10.tar.gz

用於Linux平臺
https://github.com/chokkan/liblbfgs
用於Windows平臺

2、liblbfgs原始碼解析

2.1、主要的結構

在liblbfgs中，主要的程式碼包括

  • liblbfgs-1.10/include/lbfgs.h：標頭檔案
  • liblbfgs-1.10/lib/lbfgs.c：具體的實現
  • liblbfgs-1.10/lib/arithmetic_ansi.h(另兩個arithmetic_sse_double.h和arithmetic_sse_float.h是兩個彙編編寫的等價形式)：相當於一些工具
  • liblbfgs-1.10/sample/sample.c
    ：測試樣例

2.2、工具arithmetic_ansi.h

在arithmetic_ansi.h檔案中，主要是對向量（vector）的一些操作，這部分的程式程式碼比較簡單，在這裡簡單對沒個函式的作用進行描述，包括：

  • 申請size大小的空間，同時對其進行初始化
void* vecalloc(size_t size)
  
    
   
  • 1
    •
  • 釋放空間
void vecfree(void *memblock)
  
    
   
  • 1
    •
  • 將向量x中的值設定為c
void vecset(lbfgsfloatval_t *x, const
 
 lbfgsfloatval_t c, const int n)
  
    
   
  • 1
    •
  • 將向量x中的值複製到向量y中
void veccpy(lbfgsfloatval_t *y, const lbfgsfloatval_t *x, const int n)
  
    
   
  • 1
    •
  • 取向量x中的每個值的負數，將其放到向量y中
void vecncpy(lbfgsfloatval_t *y, const lbfgsfloatval_t *x, const int n)
  
    
   
  • 1
    •
  • 對向量y中的每個元素增加向量x中對應元素的c倍
void vecadd(lbfgsfloatval_t *y, const lbfgsfloatval_t *x, const lbfgsfloatval_t c, const int n)
  
    
   
  • 1
    •
  • 計算向量x和向量y的差
void vecdiff(lbfgsfloatval_t *z, const lbfgsfloatval_t *x, const lbfgsfloatval_t *y, const int n)
  
    
   
  • 1
    •
  • 向量與常數的積
void vecscale(lbfgsfloatval_t *y, const lbfgsfloatval_t c, const int n)
  
    
   
  • 1
    •
  • 向量的外積
void vecmul(lbfgsfloatval_t *y, const lbfgsfloatval_t *x, const int n)
  
    
   
  • 1
    •
  • 向量的點積
void vecdot(lbfgsfloatval_t* s, const lbfgsfloatval_t *x, const lbfgsfloatval_t *y, const int n)
  
    
   
  • 1
    •
  • 向量的點積的開方
void vec2norm(lbfgsfloatval_t* s, const lbfgsfloatval_t *x, const int n)
  
    
   
  • 1
    •
  • 向量的點積的開方的倒數
void vec2norminv(lbfgsfloatval_t* s, const lbfgsfloatval_t *x, const int n)
  
    
   
  • 1
    •

2.3、L-BFGS演算法的主要函式

在liblbfgs中，有很多利用匯編語言優化的程式碼，這裡暫且不考慮這些優化的程式碼，對於這些優化的程式碼，作者提供了基本的實現方式。

2.3.1、為變數分配和回收記憶體空間

函式lbfgs_malloc是為優化函式中的變數分配記憶體空間的函式，其具體形式為：

// 為變數分配空間
lbfgsfloatval_t* lbfgs_malloc(int n)
{
// 涉及到彙編的一些知識，暫且不考慮
#if     defined(USE_SSE) && (defined(__SSE__) || defined(__SSE2__))
    n = round_out_variables(n);
#endif/*defined(USE_SSE)*/
    // 分配n個大小的記憶體空間
    return (lbfgsfloatval_t*)vecalloc(sizeof(lbfgsfloatval_t) * n);
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    • 
   
  • 7
    • 
   
  • 8
    • 
   
  • 9
    • 
   
  • 10
    •

函式lbfgs_malloc用於為變數分配長度為n的記憶體空間，其中，lbfgsfloatval_t為定義的變數的型別，其定義為float或者是double型別：

#if     LBFGS_FLOAT == 32
typedef float lbfgsfloatval_t;

#elif   LBFGS_FLOAT == 64
typedef double lbfgsfloatval_t;

#else
#error "libLBFGS supports single (float; LBFGS_FLOAT = 32) or double (double; LBFGS_FLOAT=64) precision only."

#endif
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    • 
   
  • 7
    • 
   
  • 8
    • 
   
  • 9
    • 
   
  • 10
    •

與記憶體分配對應的是記憶體的回收，其具體形式為：

// 釋放變數的空間
void lbfgs_free(lbfgsfloatval_t *x)
{
    vecfree(x);
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    •

2.3.2、L-BFGS中引數的初始化

函式lbfgs_parameter_init提供了L-BFGS預設引數的初始化方法。

其實在L-BFGS的演算法過程中也回提供預設的引數的方法，所以該方法有點多餘。

// 預設初始化lbfgs的引數
void lbfgs_parameter_init(lbfgs_parameter_t *param)
{
    memcpy(param, &_defparam, sizeof(*param));// 使用預設的引數初始化
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    •

函式lbfgs_parameter_init將預設引數_defparam複製到引數param中，lbfgs_parameter_t是L-BFGS引數的結構體，其具體的程式碼如下所示：

作者在這部分程式碼中的註釋寫得特別詳細，從這些註釋中可以學習到很多調參時的重要資訊。

2.3.3、L-BFGS演算法的核心過程概述

函式lbfgs是優化演算法的核心過程，其函式的引數為：

int n,// 變數的個數
lbfgsfloatval_t *x,// 變數
lbfgsfloatval_t *ptr_fx,// 目標函式值
lbfgs_evaluate_t proc_evaluate,// 計算目標函式值和梯度的回撥函式
lbfgs_progress_t proc_progress,// 處理計算過程的回撥函式
void *instance,// 資料
lbfgs_parameter_t *_param// L-BFGS的引數
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    • 
   
  • 7
    •

該函式通過呼叫兩個函式proc_evaluate和proc_progress用於計算具體的函式以及處理計算過程中的一些工作。

在函式lbfgs中，其基本的過程為：

這裡寫圖片描述

2.3.4、引數的宣告和初始化

在初始化階段涉及到很多引數的宣告，接下來將詳細介紹每一個引數的作用。

2.3.5、迴圈求解的過程

迴圈的求解過程從for迴圈開始，在for迴圈中，首先需要利用線搜尋策略進行最優的步長選擇，其具體的過程如下所示：

/* Store the current position and gradient vectors. */
// 儲存當前的變數值和梯度值
veccpy(xp, x, n);// 將當前的變數值複製到向量xp中
veccpy(gp, g, n);// 將當前的梯度值複製到向量gp中

/* Search for an optimal step. */
// 線搜尋策略，搜尋最優步長
if (param.orthantwise_c == 0.) {// 無L1正則
    ls = linesearch(n, x, &fx, g, d, &step, xp, gp, w, &cd, &param);// gp是梯度
} else {// 包含L1正則
    ls = linesearch(n, x, &fx, g, d, &step, xp, pg, w, &cd, &param);// pg是偽梯度
    // 計算偽梯度
    owlqn_pseudo_gradient(
                pg, x, g, n,
                param.orthantwise_c, param.orthantwise_start, param.orthantwise_end
                );
}
if (ls < 0) {// 已達到終止條件
    // 由於線上搜尋的過程中更新了向量x和向量g，因此從xp和gp中恢復變數值和梯度值
    /* Revert to the previous point. */
    veccpy(x, xp, n);
    veccpy(g, gp, n);
    ret = ls;
    goto lbfgs_exit;// 釋放資源
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    • 
   
  • 7
    • 
   
  • 8
    • 
   
  • 9
    • 
   
  • 10
    • 
   
  • 11
    • 
   
  • 12
    • 
   
  • 13
    • 
   
  • 14
    • 
   
  • 15
    • 
   
  • 16
    • 
   
  • 17
    • 
   
  • 18
    • 
   
  • 19
    • 
   
  • 20
    • 
   
  • 21
    • 
   
  • 22
    • 
   
  • 23
    • 
   
  • 24
    • 
   
  • 25
    •

由於線上搜尋的過程中會對變數x以及梯度的向量g修改，因此在進行線搜尋之前，先將變數x以及梯度g儲存到另外的向量中。引數param.orthantwise_c表示的是L1正則的引數，若為0則不使用L1正則，即使用L-BFGS演算法；若不為0，則使用L1正則，即使用OWL-QN演算法。

關於線搜尋的具體方法，可以參見2.3.6。
對於owlqn_pseudo_gradient函式，可以參見2.3.4

在OWL-QN中，由於在某些點處不存在導數，因此使用偽梯度代替L-BFGS中的梯度。

2.3.6、迴圈的終止條件

在選擇了最優步長過程中，會同時對變數進行更新，第二步即是判斷此時的更新是否滿足終止條件，終止條件分為以下三類：

  • 是否收斂
vec2norm(&xnorm, x, n);// 平方和的開方
if (param.orthantwise_c == 0.) {// 非L1正則
    vec2norm(&gnorm, g, n);
} else {// L1正則
    vec2norm(&gnorm, pg, n);
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    • 
  
// 判斷是否收斂
if (xnorm < 1.0) xnorm = 1.0;
if (gnorm / xnorm <= param.epsilon) {
    /* Convergence. */
    ret = LBFGS_SUCCESS;
    break;
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    • 
   
  • 7
    •

收斂的判斷方法為：

|g(x)|max(1,|x|)<ε|g(x)|max(1,|x|)<ε

如果上式滿足，則表示已滿足收斂條件。

  • 目標函式值是否有足夠大的下降（最小問題）
if (pf != NULL) {// 終止條件
    /* We don't test the stopping criterion while k < past. */
    // k為迭代次數，只考慮past>k的情況，past是指只保留past次的值
    if (param.past <= k) {
        /* Compute the relative improvement from the past. */
        // 計算函式減小的比例
        rate = (pf[k % param.past] - fx) / fx;

        /* The stopping criterion. */
        // 下降比例是否滿足條件
        if (rate < param.delta) {
            ret = LBFGS_STOP;
            break;
        }
    }

    /* Store the current value of the objective function. */
    // 更新新的目標函式值
    pf[k % param.past] = fx;
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    • 
   
  • 7
    • 
   
  • 8
    • 
   
  • 9
    • 
   
  • 10
    • 
   
  • 11
    • 
   
  • 12
    • 
   
  • 13
    • 
   
  • 14
    • 
   
  • 15
    • 
   
  • 16
    • 
   
  • 17
    • 
   
  • 18
    • 
   
  • 19
    • 
   
  • 20
    •

在pf中，儲存了param.past次的目標函式值。計算的方法為：

fo−fnfn<Δfo−fnfn<Δ

  • 是否達到最大的迭代次數
// 已達到最大的迭代次數
if (param.max_iterations != 0 && param.max_iterations < k+1) {
    /* Maximum number of iterations. */
    ret = LBFGSERR_MAXIMUMITERATION;
    break;
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    •

如果沒有滿足終止的條件，那麼需要擬合新的Hessian矩陣。

2.3.7、擬合Hessian矩陣

在BFGS演算法（優化演算法——擬牛頓法之BFGS演算法）中，其Hessian矩陣為：

Hk+1=(I−skyTkyTksk)THk(I−yksTkyTksk)+sksTkyTkskHk+1=(I−skykTykTsk)THk(I−ykskTykTsk)+skskTykTsk

其中，yk=▽f(xk+1)−▽f(xk)yk=▽f(xk+1)−▽f(xk)步向量即可。其具體的計算方法為：

這裡寫圖片描述

L-BFGS的具體原理可以參見“優化演算法——擬牛頓法之L-BFGS演算法”。

在上述過程中，第一個迴圈計算出倒數第mm代時的下降方向，第二個階段利用上面計算出的方法迭代計算出當前的下降方向。

根據上述的流程，開始擬合Hessian矩陣：

  • 計算向量序列{sk}{sk}
// 更新s向量和y向量
it = &lm[end];// 初始時，end為0
vecdiff(it->s, x, xp, n);// x - xp，xp為上一代的值，x為當前的值
vecdiff(it->y, g, gp, n);// g - gp，gp為上一代的值，g為當前的值
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    •
  • 兩個迴圈
// 通過擬牛頓法計算Hessian矩陣
// L-BFGS的兩個迴圈
j = end;
for (i = 0;i < bound;++i) {
    j = (j + m - 1) % m;    /* if (--j == -1) j = m-1; */
    it = &lm[j];
    /* \alpha_{j} = \rho_{j} s^{t}_{j} \cdot q_{k+1}. */
    vecdot(&it->alpha, it->s, d, n);// 計算alpha
    it->alpha /= it->ys;// 乘以rho
    /* q_{i} = q_{i+1} - \alpha_{i} y_{i}. */
    vecadd(d, it->y, -it->alpha, n);// 重新修正d
}

vecscale(d, ys / yy, n);

for (i = 0;i < bound;++i) {
    it = &lm[j];
    /* \beta_{j} = \rho_{j} y^t_{j} \cdot \gamma_{i}. */
    vecdot(&beta, it->y, d, n);
    beta /= it->ys;// 乘以rho
    /* \gamma_{i+1} = \gamma_{i} + (\alpha_{j} - \beta_{j}) s_{j}. */
    vecadd(d, it->s, it->alpha - beta, n);
    j = (j + 1) % m;        /* if (++j == m) j = 0; */
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    • 
   
  • 7
    • 
   
  • 8
    • 
   
  • 9
    • 
   
  • 10
    • 
   
  • 11
    • 
   
  • 12
    • 
   
  • 13
    • 
   
  • 14
    • 
   
  • 15
    • 
   
  • 16
    • 
   
  • 17
    • 
   
  • 18
    • 
   
  • 19
    • 
   
  • 20
    • 
   
  • 21
    • 
   
  • 22
    • 
   
  • 23
    • 
   
  • 24
    •

其中，ys和yy的計算方法如下所示：

vecdot(&ys, it->y, it->s, n);// 計算點積
vecdot(&yy, it->y, it->y, n);
it->ys = ys;
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    •

bound和end的計算方法如下所示：

bound = (m <= k) ? m : k;// 判斷是否有足夠的m代
++k;
end = (end + 1) % m;
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    •

2.3.8、線搜尋策略

在liblbfgs中涉及到大量的線搜尋的策略，線搜尋的策略主要作用是找到最優的步長。我們將在下一個主題中進行詳細的分析。

補充

1、回撥函式

回撥函式就是一種利用函式指標進行函式呼叫的過程。回撥函式的好處是具體的計算過程以函式指標的形式傳遞給其呼叫處，這樣可以較方便地對呼叫函式進行擴充套件。

假設有個print_result函式，需要輸出兩個int型數的和，那麼直接寫即可，如果需要改成差，那麼得重新修改；如果在print_result函式的引數中傳入一個函式指標，具體的計算過程在該函式中實現，那麼就可以在不改變print_result函式的條件下對功能進行擴充，如下面的例子：

  • frame.h
#include <stdio.h>

void print_result(int (*get_result)(int, int), int a, int b){
    printf("the final result is : %d\n", get_result(a, b));
}

  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    •
  • process.cc
#include <stdio.h>
#include "frame.h"

int add(int a, int b){
    return a + b;
}

int sub(int a, int b){
    return a - b;
}

int mul(int a, int b){
    return a * b;
}

int max(int a, int b){
    return (a>b?a:b);
}

int main(){
    int a = 1;
    int b = 2;
    print_result(add, a, b);
    print_result(sub, a, b);
    print_result(mul, a, b);
    print_result(max, a, b);
    return 1;
}
  
    
   
  • 1
    • 
   
  • 2
    • 
   
  • 3
    • 
   
  • 4
    • 
   
  • 5
    • 
   
  • 6
    • 
   
  • 7
    • 
   
  • 8
    • 
   
  • 9
    • 
   
  • 10
    • 
   
  • 11
    • 
   
  • 12
    • 
   
  • 13
    • 
   
  • 14
    • 
   
  • 15
    • 
   
  • 16
    • 
   
  • 17
    • 
   
  • 18
    • 
   
  • 19
    • 
   
  • 20
    • 
   
  • 21
    • 
   
  • 22
    • 
   
  • 23
    • 
   
  • 24
    • 
   
  • 25
    • 
   
  • 26
    • 
   
  • 27
    • 
   
  • 28
    •

參考文獻

轉載自:https://www.baidu.com/link?url=HdT5_VBKjQpIwXmJOwKps0amX4Kx643we2GUNYQWhT3xQZOTHDlzv4jEx2cQ1UajqgAguxwgvS8Q75KH42jQ1mDEc6Q9aQR59JeQPwOTcLG&wd=&eqid=a2ba07d6000696c8000000045bc5a9ca

相關推薦

機器學習演算法實現解析——liblbfgs之L-BFGS演算法

在博文“優化演算法——擬牛頓法之L-BFGS演算法”中，已經對L-BFGS的演算法原理做了詳細的介紹，本文主要就開原始碼liblbfgs重新回顧L-BFGS的演算法原理以及具體的實現過程，在L-BFGS演算法中包含了處理L1正則的OWL-QN演算法，對於OWL-QN演算法的詳細原理，可以參見

優化演算法——擬牛頓法之L-BFGS演算法

一、BFGS演算法利用Sherman-Morrison公式可對上式進行變換，得到令，則得到：二、BGFS演算法存在的問題    在BFGS演算法中，每次都要儲存近似Hesse矩陣，在高維資料時，儲存浪費

機器學習系列文章：Apriori關聯規則分析演算法原理分析與程式碼實現

1.關聯規則淺談     關聯規則（Association Rules）是反映一個事物與其他事物之間的相互依存性和關聯性，如果兩個或多個事物之間存在一定的關聯關係，那麼，其中一個事物就能通過其他事物預測到。關聯規則是資料探勘的一個重要技術，用於從大量資料中挖掘出有價值的資料

機器學習實戰（第二篇）-k-近鄰演算法Python實現

      上一篇幅中，我們介紹了k-近鄰演算法的基本概念、具體的分析步驟和分析方法，本篇中我們將介紹如何通過Python工具實現一個k-近鄰演算法。 1. 準備-使用Python匯入資料     首

《web安全之機器學習入門》第5章K近鄰演算法讀書筆記【下】

Rootkit是一種特殊的惡意軟體，它的功能是在安裝目標上隱藏自身及指定的檔案、程序和網路連線等資訊。待分析資料集：KDD-99資料集，連結：http://kdd.ics.uci.edu/databases/kddcup99/kddcup99.html該資料集是從一個模擬的美

《web安全之機器學習入門》第5章K近鄰演算法讀書筆記【上】

K近鄰演算法的思路：如果一個樣本在空間上最近的K鄰居大多數都屬於M類，則該樣本屬於M類。在本章中，使用K近鄰演算法識別使用者操作序列中的異常命令。分析資料集url:http://www.schonlau.net/資料集說明：50個使用者的linux操作日誌以User開頭的檔案

《機器學習實戰》學習筆記（十）之使用Apriori演算法進行關聯

轉載請註明作者和出處：http://blog.csdn.net/john_bh/ 執行平臺： Windows Python版本： Python3.6 IDE： Sublime text3 背景 一、關聯分析 二、Apriori原理

步步學習之用python實戰機器學習1－kNN （K-NearestNeighbors）演算法（a）

我最近才開始接觸機器學習，我大學數學學的幾乎忘了，最近才接觸python。所以我以一個完全初學者角度來學習機器學習。 我主要用的書籍就是machine learning in action （機器學習實戰）這本書。我主要是用文中已有的程式碼來講解機器學習。 同時對程式碼進行

R語言學習系列(資料探勘之決策樹演算法實現--ID3程式碼篇)

轉載自：http://blog.csdn.net/hawksoft/article/details/7760868 1、輔助類，用於計算過程和結果儲存 [csharp] view plaincopyprint? /// &

分散式機器學習的叢集方案介紹之HPC實現

機器學習的基本概念機器學習方法是計算機利用已有的資料（經驗），得出了某種模型(遲到的規律)，並利用此模型預測未來(是否遲到)的一種方法。目前機器學習廣泛應用於廣告投放、趨勢預測、影象識別、語音識別、自動駕駛和產品推薦等眾多領域。在確定了問題模型之後，根據已知資料尋找模型引數的

周志華《機器學習》Ch9. 聚類：k-means演算法的python實現

理論 k-means方法是一種常用的聚類方法，其目標是最小化 其中是第i個簇的中心。直接優化上式有難度，故k-means演算法採用一種近似方法。 簡單來說，k-means演算法由兩個步驟迴圈組成： 1. 計算每個sample到各個簇中心的距離，將該sample的類

機器學習Python實現之線性模型

本文將詳細解釋線性分類的幾個常用模型：線性迴歸、對數迴歸、對數機率迴歸，並簡要介紹其優化方法。文末附有Python程式碼實現。如果問題，歡迎留言交流～ 線性迴歸（linear regression） 模型 設樣本表示為d維列向量x，其標記為y，記x

機器學習Python實現AdaBoost

出了 .py learn tle 基礎 向量 adsi pad del adaboost是boosting方法多個版本號中最流行的一個版本號，它是通過構建多個弱分類器。通過各個分類器的結果加權之後得到分類結果的。這裏構建多個分類器的過程也是有講究的，通過關註之前構建的分

機器學習環境配置系列一之CUDA

arch developer 完成 用戶 uname sed a10 是否 安裝 本文配置的環境為redhat6.9+cuda10.0+cudnn7.3.1+anaonda6.7+theano1.0.0+keras2.2.0+jupyter遠程，其中cuda的版本為10.0

「機器學習」Python資料分析之Numpy進階

請點選此處輸入圖片描述 進階 廣播法則(rule) 廣播法則能使通用函式有意義地處理不具有相同形狀的輸入。 廣播第一法則是，如果所有的輸入陣列維度不都相同，一個“1”將被重複地新增在維度較小的陣列上直至所有的陣列擁有一樣的維度。 廣播第二法則確定長度為1的陣列沿著特

「機器學習」Python資料分析之Numpy

請點選此處輸入圖片描述 NumPy的主要物件是同種元素的多維陣列。這是一個所有的元素都是一種型別、通過一個正整數元組索引的元素表格(通常是元素是數字)。在NumPy中維度(dimensions)叫做軸(axes)，軸的個數叫做秩(rank)。 例如，在3D空間一個點的座標[1,

機器學習筆記 第5課：線性迴歸演算法

線性迴歸可能是統計學和機器學習中最知名且易於理解的演算法之一。 它不就是一項起源於統計學的技術嗎？ 預測建模主要關注的是讓模型的誤差最小化，或者說，在可以解釋的前提下，儘可能作出最準確的預測。我們會借用，重用，甚至是竊取許多不同領域（包括統計學）的演算法，並將其用於上述的目標。 線性迴歸

《機器學習實戰》第七章----AdaBoost元演算法

元演算法 元演算法是對其他演算法進行組合的一種方法,其背後的思路就是組合多個專家的經驗來得到最終的結論,類似於我們的投票.而提升方法是其中最常用的方法,在分類問題中,它通過改變訓練樣本的權重,學習多個分類器,並將這些這些分類器進行線性組合. 弱分類器和強分類器 關於Ad

機器學習：效能度量指標之查準率和查全率

    在很多實際應用中，我們知道僅僅關心正確分類的結果是不夠的，並且，在資料偏斜比較嚴重的情況下，模型準確率可能具有相當程度的誤導性，我們也需要知道資料被錯誤分類的情況，以確認為此需要承擔的分類錯誤的代價。（False Positive假陽性和False Negative假

機器學習5：邏輯迴歸之多分類Multi-class classification

上一節講解了邏輯迴歸中的二分類問題的原理與步驟，本節講解多分類問題。 以三個class分類為例，過程如圖所示： 原理性推導省略。 1、如圖1所示，對於每個類別，各分配一個線性模型，通過softmax處理得到每個類別的輸出概率y，且所有y的和等於1； 2、如圖2所示，輸出的