機器學習筆試題精選 知識點
參考:
https://blog.csdn.net/red_stone1?t=1
1.留一法,簡單來說就是假設有 N 個樣本,將每一個樣本作為測試樣本,其它 N-1 個樣本作為訓練樣本。這樣得到 N 個分類器,N 個測試結果。用這 N個結果的平均值來衡量模型的效能。
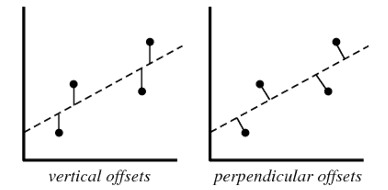
2.線性迴歸模型計算損失函式,例如均方差損失函式時,使用的都是 vertical offsets。perpendicular offsets 一般用於主成分分析(PCA)中。如圖所示:
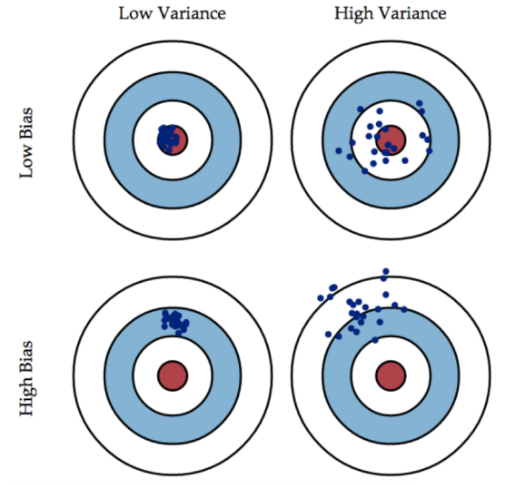
3.偏差(bias)可以看成模型預測與真實樣本的差距,想要得到 low bias,就得複雜化模型,但是容易造成過擬合。方差(variance)可以看成模型在測試集上的表現,想要得到 low variance,就得簡化模型,但是容易造成欠擬合。
如果模型過於簡單,通常會造成欠擬合,伴隨著高偏差、低方差;如果模型過於複雜,通常會造成過擬合,伴隨著低偏差、高方差。
3. 如果資料量較少,容易在假設空間找到一個模型對訓練樣本的擬合度很好,容易造成過擬合,該模型不具備良好的泛化能力。
如果假設空間較小,包含的可能的模型就比較少,也就不太可能找到一個模型能夠對樣本擬合得很好,容易造成高偏差、低方差,即欠擬合。
4.Lasso 迴歸其實就是在普通線性迴歸的損失函式的基礎上增加了個 β 的約束,第一範數約束下,β 更有可能被約束成 0, 因此,Lasso 迴歸適用於樣本數量較少,特徵維度較大的情形,便於從較多特徵中進行特徵選擇。例如 DNA 資料,特徵維度很大,我們只希望通過 Lasso 迴歸找出與某些疾病有關的 DNA 片段,Lasso 迴歸會讓一部分迴歸係數剛好可以被約束為 0,起到特徵選擇的效果。
5. Ridge 迴歸又稱嶺迴歸,它是普通線性迴歸加上 L2 正則項,用來防止訓練過程中出現的過擬合。L2 正則化效果,限定區域是圓,這樣,得到的迴歸係數為 0 的概率很小,很大概率是非零的。因此,比較來說,Lasso 迴歸更容易得到稀疏的迴歸係數,有利於捨棄冗餘或無用特徵,適用於特徵選擇。
6. 如果線上性迴歸模型中增加一個特徵變數,下列可能發生的是(多選)?
A. R-squared 增大,Adjust R-squared 增大 B. R-squared 增大,Adjust R-squared 減小 C. R-squared 減小,Adjust R-squared 減小 D. R-squared 減小,Adjust R-squared 增大
**答案**:AB *R-Squared 反映的是大概有多準,因為,隨著樣本數量的增加,R-Squared 必然增加,無法真正定量說明準確程度,只能大概定量。 單獨看 R-Squared,並不能推斷出增加的特徵是否有意義。通常來說,增加一個特徵特徵,R-Squared 可能變大也可能保持不變,兩者不一定呈正相關。 如果使用校正決定係數(Adjusted R-Squared),增加一個特徵變數,如果這個特徵有意義,Adjusted R-Square 就會增大,若這個特徵是冗餘特徵,Adjusted R-Squared 就會減小。分子部分表示真實值與預測值的平方差之和,類似於均方差 MSE;分母部分表示真實值與均值的平方差之和,類似於方差 Var。
均方誤差:MSE=1m∑i=1m(y(i)−y^(i))2
評價均方誤差:MAE=1m∑i=1m|y(i)−y^(i)|
7.求解線性迴歸係數,我們一般最常用的方法是梯度下降,利用迭代優化的方式。除此之外,還有一種方法是使用正規方程,原理是基於最小二乘法。下面對正規方程做簡要的推導。
已知線性迴歸模型的損失函式 Ein 為:
Ein=1m(XW−Y)2
Ein=1m(XW−Y)2
對 Ein 計算導數,令 ∇Ein=0:
∇Ein=2m(XTXW−XTY)=0
∇Ein=2m(XTXW−XTY)=0
然後就能計算出 W:W=(XTX)−1XTY
W=(XTX)−1XTY
以上就是使用正規方程求解係數 W 的過程。可以看到,正規方程求解過程不需要學習因子,也沒有迭代訓練過程。當特徵數目很多的時候,XTXXTX 矩陣求逆會很慢,這時梯度下降演算法更好一些。
8.相關係數 r=0 只能說明兩個變數之間不存線上性關係,仍然可能存在非線性關係。
9.SSE 是平方誤差之和(Sum of Squared Error)
10.
相關(Correlation)是計算兩個變數的線性相關程度,是對稱的。也就是說,x 與 y 的相關係數和 y 與 x 的相關係數是一樣的,沒有差別。
迴歸(Regression)一般是利用 特徵 x 預測輸出 y,是單向的、非對稱的。