題目背景

有一天，小貓rainbow和freda來到了湘西張家界的天門山玉蟾宮，玉蟾宮宮主藍兔盛情地款待了它們，並賜予它們一片土地。

題目描述

這片土地被分成N*M個格子，每個格子裡寫著'R'或者'F'，R代表這塊土地被賜予了rainbow，F代表這塊土地被賜予了freda。

現在freda要在這裡賣萌。。。它要找一塊矩形土地，要求這片土地都標著'F'並且面積最大。

但是rainbow和freda的OI水平都弱爆了，找不出這塊土地，而藍兔也想看freda賣萌（她顯然是不會程式設計的……），所以它們決定，如果你找到的土地面積為S，它們每人給你S兩銀子。

輸入輸出格式

第一行兩個整數N,M，表示矩形土地有N行M列。

接下來N行，每行M個用空格隔開的字元'F'或'R'，描述了矩形土地。

輸出一個整數，表示你能得到多少銀子，即(3*最大'F'矩形土地面積)的值。

輸入輸出樣例

5 6 
R F F F F F 
F F F F F F 
R R R F F F 
F F F F F F 
F F F F F F

45

說明

對於50%的資料，1<=N,M<=200

對於100%的資料，1<=N,M<=1000

題解

這是來自我校學長(祖傳)的並查集做法

首先從上到下列舉每一行（分割線）。

在當前行，把它以上的F染色，那麼F會構成這樣的圖案↓

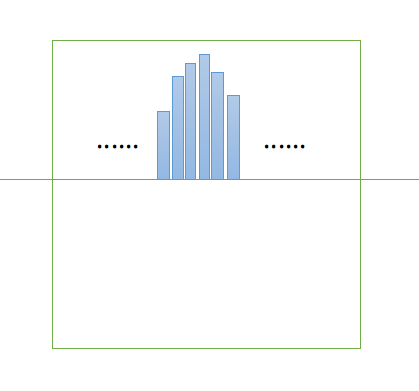
每一列在這條分割線以上有多少連續的F，可以在每次下移分割線時順便用O(m)掃一遍維護。（如果這一格為F，那麼連續F為之前這列的連續F加1;否則為0）

然後我們按照每一列的F高度排序，每次把F最高的取出來。

如果它左邊一列被取過了，我們就把當前列和它左邊一列並起來;如果右邊一列被取過，就把這一列和右邊一列並起來。

最後詢問一下這一列的祖先有多少個子節點，也就是這一列以它的高度往左右最多能擴充套件的寬度。

原理：在當前列之前被併入這個祖先的列的長度一定大於等於當前列的長度，並且這些列互相相鄰。

然後當前列的高度，乘上它往左右最多能擴充套件的寬度，就是取這一列，且高度等於這一列的最大矩形面積了。(就算還有相同高度的沒有處理，之後做那一列的時候也會得到最優解)

實現的時候只需要把兩個需要合併的列的祖先節點$fa[v]=u,siz[u]+=siz[v]$就可以了，因為只有祖先節點的siz是有意義的。

因為懶所以直接用了優先佇列，並查集只路徑壓縮也是$O(mlogm)$的時間，總複雜度$O(nmlogm)$

 1 /*
 2     qwerta
 3     P4147 玉蟾宮
 4     Accepted
 5     100
 6     程式碼 C++，1.14KB
 7     提交時間 2018-10-14 22:07:46
 8     耗時/記憶體
 9     1724ms, 916KB
10 */
11 #include<iostream>
12 #include<cstdio>
13 #include<queue>
14 using namespace std;
15 int s[1003];//記錄每列往上F的高度
16 int fa[1003],siz[1003];//並查集
17 bool sf[1003];//標記每一列是否被用過
18 struct emm{
19     int nod,v;
20 };
21 struct cmp{
22     bool operator()(emm qaq,emm qwq){
23         return qaq.v<qwq.v;
24     }
25 };//過載()運算子（用來給優先佇列排序
26 priority_queue<emm,vector<emm>,cmp>q;
27 int fifa(int x)
28 {
29     if(fa[x]==x)return x;
30     return fa[x]=fifa(fa[x]);
31 }
32 void con(int x,int y)//把x列和y列並起來
33 {
34     int u=fifa(x),v=fifa(y);
35     fa[v]=u;
36     siz[u]+=siz[v];
37     return;
38 }
39 int main()
40 {
41     //freopen("a.in","r",stdin);
42     ios::sync_with_stdio(false);
43     cin.tie(false),cout.tie(false);//關閉同步流（讓cin變快
44     int n,m;
45     cin>>n>>m;
46     int ans=0;
47     for(int c=1;c<=n;++c)//從上往下移分割線
48     {
49         for(int i=1;i<=m;++i)
50         {
51             char ch;
52             cin>>ch;
53             if(ch=='F'){s[i]++;q.push((emm){i,s[i]});}
54             else s[i]=0;
55         }
56         for(int i=1;i<=m;++i)
57         fa[i]=i,siz[i]=1,sf[i]=0;//初始化
58         while(!q.empty())
59         {
60             int i=q.top().nod,x=q.top().v;q.pop();
61             sf[i]=1;//標記這一列取過了
62             if(sf[i-1])con(i-1,i);//如果左邊取過了就並起來
63             if(sf[i+1])con(i,i+1);//如果右邊取過了就並起來
64             int fi=fifa(i);//找祖先節點
65             ans=max(ans,siz[fi]*x);
66         }
67     }
68     cout<<ans*3;//輸出最大矩形面積*3
69     return 0;
70 }