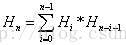(轉)各種排列組合的數的公式和推導
原貼地址:https://blog.csdn.net/qq_36808030/article/details/75045129?utm_source=blogxgwz0
一、排列(在乎順序)
全排列:P(n,n)=n!
n個人都排隊。第一個位置可以選n個,第二位置可以選n-1個,以此類推得: P(n,n)=n*(n-1)*…*3*2*1= n!
部分排列:P(n,m)=n!/(n-m)!
n個人,選m個出來排隊,第一個位置可以選n個,…,最後一個可以選n-m+1個,以此類推得:P(n,m)=n*(n-1)*...*(n-m+1)=n!/(n-m)!。
二、組合(不在乎順序)
n個人,選m個人出來。
因為不在乎順序,所以按排列算的話,每個組合被選到之後還要排列,是被算了m!遍的。即C(n,m)*m!=P(n,m)
故而得:C(n,m)=n!/(m!*(n-m)!)
有兩條性質:
1、C(n,m)=C(n,n-m)。就是說 從n個裡面選m個 跟 從n個裡面選n-m個出來不選它 是一樣的。
2、C(n,m)=C(n-1,m)+C(n-1,m-1)。遞推式..
從n個裡面選m個出來的方案=從n-1個裡面選m個的方案(即不選第n個) + 從n-1個裡面選m-1個的方案(即選第n個)
三、圓排列
圓排:Q(n,n)=(n-1)!
n個人坐成一圈有多少種坐法。
想想坐成一圈後,分別以每個位置為頭斷開,可以排成一個序列,就是將n個人全排列中的一種。這樣可以得到n個序列,但是在圓排中是視為同一種坐法的。所以:Q(n,n)*n=P(n,n),即Q(n,n)=P(n,n)/n=n!/n=(n-1)!
部分圓排:Q(n,m)=P(n,m)/m=n!/(m*(n-m)!)
推導類似
四、重複排列(有限個):n!/(a1!*a2!*…*ak!)
k種不一樣的球,每種球的個數分別是a1,a2,...ak,設n=a1+a2+…+ak,求這n個球的全排列數。
把每種球重複的除掉就好了。假如第一種球有a1個,那麼看成都是不一樣的話就有a1!種排列方法,然而它們都是一樣的,就是說重複了a1!次。其它的一樣,所以重複排列的公式就是n!/(a1!*a2!*…*ak!)
五、重複組合(無限個):C(n+k-1,k)
n種不一樣的球,每種球的個數是無限的,從中選k個出來的方案數。
看了幾種證法,寫兩種吧。
證明1:這個是比較常見的。。然而我不是特別懂為什麼可以。。
給這n個球編號為1~n,選出來k個。
設為1≤a1≤a2≤a3≤...≤ak≤n,因為是組合,排下序也沒什麼關係。
可能重複,所以有等號。但是普通的組合是沒有等號的,所以要把等號想辦法去掉。
於是設bi=ai+i-1。[為什麼可以加,這樣還表示編號嗎?
這樣就保證了{b}都是不一樣的。
故得1<b1<b2<...<bk<n+k-1
即相當於從n+k-1個球中選k個出來,為C(n+k-1,k).
證明2:轉化為隔板法啊很機智!看這個看懂了!
選出來了k個球,我們就設本來就有n+k個,而這n+k個球只有n種不同的種類,就=把這n+k個球分進不同的n個盒子裡,但保證每個盒子不為空=把n+k個數分成不為空的n塊=在n+k-1個間隔中放n-1個隔板(來分)。即C(n+k-1,n-1)=C(n+k-1,k),(根據性質1。
六、不相鄰組合:C(n-k+1,k)
1~n這n個自然數中選k個,這k個數中任何兩個數不相鄰數的組合有多少種。
好像可以跟上面證明1的證法一樣來證,但是我並不會= =。
所以下面的證明是來自hyc大學霸的:
一開始先假設選出來的k個數沒有取到1和n,那麼就相當於把n-k個數分成了k+1份(因為要求要不相鄰~)。但是我們是可以選1和n的,所以給兩邊各補上一位(隨便補啦,按順序的話就是0跟n+1咯),這樣選出來的k個數都在1~n中,就相當於把n-k+2個數分成了k+1份。即在(n-k+2)-1個間隔中放k個隔板!就是C(n-k+1,k)。
七、錯排(錯位排列):dn=(n-1)*(dn-1 + dn-2),n≥3
↑是個遞推式。我只會遞推式,,好像也只有遞推式。。
(同時也有,dn=n*dn-1 + (-1)^n。沒深入探討和背過這個orz
問題相當於,有n個人編號為1~n,住在1~n號房間,要求每個人的編號與其房間號不同,問有多少種排列方法。
於是這個怎麼推導的呢?先寫成:dn=(n-1)*dn-1 + (n-1)*dn-2。
假如說一開始第i個人住在第i號房間。
①令n-1個人錯排後,第n個人與其中的一個i互換房間,即n住在i錯排後住的房間,i去住第n號房間。滿足要求啊。因為n可以和n-1個人換房間,所以有(n-1)*dn-1種方法。
②n選擇跟一個人換房間,即n住第i號房,i住第n號房,讓剩下的n-2個人自己去搞一次錯排。同樣的,n可以有n-1種選擇,這就有(n-1)*dn-2種方法。跟上一種方式是不一樣的哦!
故遞推關係就是dn=(n-1)*(dn-1 + dn-2)
錯位排列數列為 0,1,2,9,44,265,……
八、stirling數(斯特林數)
第一類stirling數:S(n,m)=S(n-1,m-1)+(n-1)*S(n-1,m).
n個不同元素構成m個圓排列
①n-1個元素構成了m-1個圓排,第n個單獨成一個圓排:S(n-1,m-1)。
②n-1個元素構成m個圓排,將第n個元素插在任一個元素的左邊:(n-1)*S(n-1,m)。
故遞推關係就是S(n,m)=S(n-1,m-1)+(n-1)*S(n-1,m)。
第二類stirling數:S(n,m)=S(n-1,m-1)+m*S(n-1,m).
n個不同元素構成m個非空的(無差別)集合
①n-1個元素構成了m-1個集合,第n個單獨成一個集合:S(n-1,m-1)。
②n-1個元素構成m個集合,第n個放進任一個集合裡:m*S(n-1,m)。
故遞推關係就是S(n,m)=S(n-1,m-1)+m*S(n-1,m)。
有些性質啊S(n,0)、S(n,1)、S(n,n)等等為一些常數的,可以自己想到的!
九、Catalan數(卡特蘭數)
通項式:Hn=C(2n,n)/(n+1)=(2n)!/( (n+1)!*n!)
組合公式:Hn=C(2n,n)-C(2n,n-1)
遞迴公式:
這個有很多人寫我就不詳細寫啦~
有很多很有用的應用!而那些應用為什麼可以用卡特蘭數來解跟這些↑式子有很大聯絡。
放些感覺比較全&有點證明/推導的連結(可能他們也是轉的orz):
http://www.360doc.com/content/14/1001/00/9482_413586206.shtml