Cohen-Sutherland直線裁剪演算法
阿新 • • 發佈:2018-11-11
在二維觀察中,需要在觀察座標系下根據視窗大小對二維圖形進行裁剪(clipping),只將位於視窗內的圖形變換到視區輸出。直線段裁剪是二維圖形裁剪的基礎,裁剪的實質是判斷直線段是否與視窗相交,如相交則進一步確定直線段上位於視窗內的部分。
編碼原理
Cohen-Sutherland直線段裁剪演算法是最早流行的編碼演算法。每段直線的端點都被賦予一組四位二進位制程式碼,稱為區域編碼(region code,RC),用來標識直線段端點相對於視窗邊界及其延長線的位置。
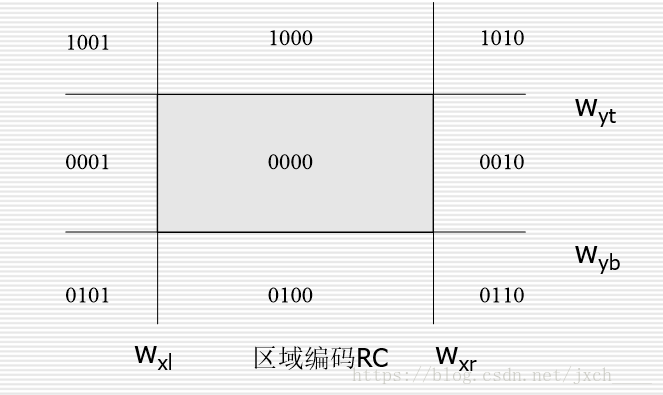
假設視窗是標準矩形,由上、下、左、右4條邊界組成,延長視窗的4條邊界形成9個區域。這樣根據直線段的任一端點P(x,y)所處的視窗區域位置,可以賦予一組4位二進位制編碼,稱為區域碼RC=C3C2C1C0。C0代表左邊界, C1代表右邊界, C2代表下邊界, C3代表上邊界。
為了保證視窗內及視窗邊界上直線段端點的編碼為零,定義規則如下:
C0:若端點的 x < wxl,則C0=1,否則C0=0。
C1:若端點的x > wxr,則C1=1,否則C1=0。
C2:若端點的y < wyb,則C2=1,否則C2=0。
C3:若端點的y > wyt,則C3=1,否則C3=0。
裁剪步驟
- 若直線段的兩個端點的區域編碼都為0,有RC0|RC1=0(二者按位相或的結果為零,即RC0=0且RC1=0),說明直線段的兩個端點都在視窗內,應“簡取”之(trivally accepted)。
- 若直線段的兩個端點的區域編碼都不為0,且RC0&RC1≠0(二者按位相與的結果不為零,即RC0≠0且RC1≠0),說明直線段位於窗外的同一側,或左方、或右方、或上方、或下方,應“簡棄”之(trivally rejected) 。
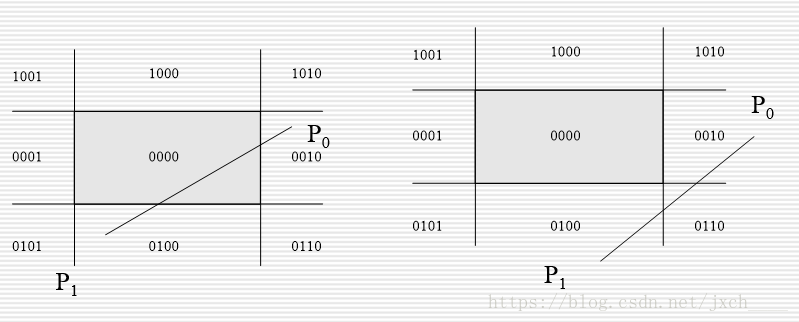
- 若直線段既不滿足“簡取”也不滿足“簡棄”的條件,則需要與視窗進行“求交”判斷。這時,直線段必然與視窗邊界或視窗邊界的延長線相交,分兩種情況處理。
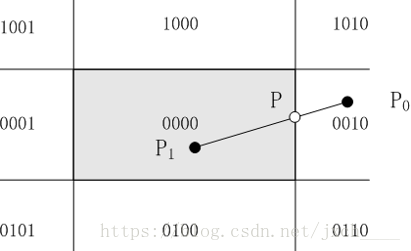
P0點的編碼為0010。P1點編碼為0000。交點P在視窗邊界上,編碼為0000。 根據編碼判斷PP1被簡取。
Cohen-sutherland演算法的關鍵技術:在於總是要讓直線段的一個頂點處於視窗之外,例如P0點。這樣P0點到交點P的直線段必然不可見,故可以直接拋棄。
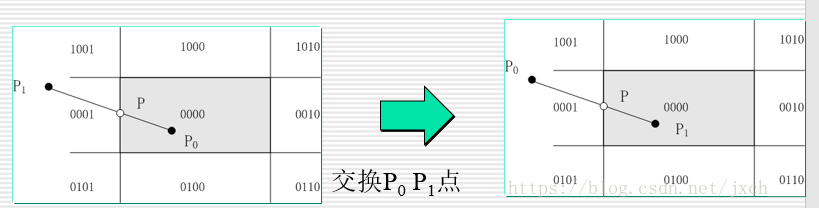
直線段必然與視窗邊界或視窗邊界的延長線相交,分兩種情況處理。
裁剪直線段時,一般按固定順序左(x=wxl),右(x=wxr)、下(y=wyb)、上(y=wyt)求解視窗邊界與直線段的交點。
交點計算公式
對於端點座標為P0(x0,y0)和P1(x1,y1)的直線段,
與視窗左邊界(x=wxl)或右邊界(x=wxr)交點的y座標的計算公式為
與視窗上邊界(y=wyt)或下邊界(y=wyb)交點的x座標的計算公式為
其中,