題意自己看題目吧，挺短的。

思考過程：昨天感覺一天不做題很對不起自己，於是晚上跑到實驗室開啟別人樹形dp的部落格做了上面最後一個HDU的題，也是個多校題。。一開始沒有頭緒了很久，因為起點不固定，所以這1e5的資料要跑的話就有很多很多轉移，但是狀態又不可能定義得很複雜。。然後後來就想到和葉子有關係。就這樣停滯不前了很久。半夜看別人部落格感覺看懂了，其實也沒比沒看部落格前多懂多少。我只想到了肯定是一個葉子到另一個葉子然後跳一下到另一個葉子然後繼續這樣做。今天中午又想了很久。首先畫樣例是關鍵，學了別人的dp寫法後來發現自己樣例都不能過。

圖一如既往的醜。

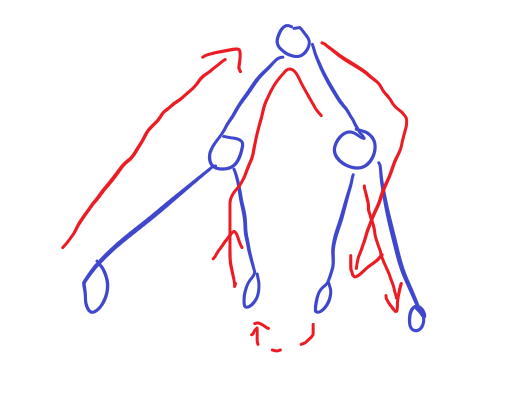
反正這個二叉樹這樣走是8的，然後只跳了一次，並不是網上別人說的什麼（葉子+1）/2。。但是確實是葉子和葉子匹配。

我們不難發現有些邊走了兩次有些邊走了一次。而dp的過程也是基於此。首先因為核心在於葉子，所以要以一個非葉子節點開始dfs。

我們考慮一個點u,他的某個兒子v，如果v有偶數個葉子，那麼u->v這條邊對答案的貢獻是2，若為奇數則為1。因為一個有偶數個葉子的兒子肯定是其中某兩個葉子去和v的祖先節點或者兄弟節點的葉子匹配最優（所花費的跳最少）。而奇數個時只有一個點需要這樣。這個不懂的自己畫一畫，我也畫了很久，太菜了。

如果總共有偶數個葉子，那麼顯然兩兩匹配，這就是答案。而若有奇數個葉子節點，就有一個點無法匹配，那麼dfs列舉一下就好了。用dp做法就是找一條只有一個葉子的最長鏈。。不是特別懂。

直接放看得懂的連結吧，喜歡dp寫法的自己百度，第一篇就是。

https://www.cnblogs.com/zufezzt/p/5796175.html

#include<bits/stdc++.h>
#define ll long long
#define pb push_back
#define _mp make_pair
#define db double
#define eps 1e-9
#define inf 1e9
using namespace std;
const int maxn=1e5+7;
inline ll read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int cnt;
int n,m;
int root;
int fir[maxn],nxt[maxn*2],to[maxn*2];
int du[maxn],siz[maxn];
int dp[maxn][2];
void add_e(int x,int y)
{
    ++cnt;nxt[cnt]=fir[x];fir[x]=cnt;to[cnt]=y;
}
void dfs1(int x,int fa)
{
    dp[x][0]=0;dp[x][1]=inf;
    siz[x]=0;
    int ts=0;
    for(int i=fir[x];i;i=nxt[i])
    {
        if(to[i]==fa)continue;
        dfs1(to[i],x);
        siz[x]+=siz[to[i]];
        int d;
        ts++;
        if(siz[to[i]]%2==0)d=2;
        else d=1;
        dp[x][0]+=dp[to[i]][0]+d;
    }
    for(int i=fir[x];i;i=nxt[i])
    {
        if(to[i]==fa)continue;
        if(siz[to[i]]==1&&ts>1)dp[x][1]=min(dp[x][1],dp[x][0]);
        if(dp[to[i]][1]>=inf)continue;
        int k=((siz[to[i]]&1)?1:-1);
        dp[x][1]=min(dp[x][1],dp[x][0]-dp[to[i]][0]+dp[to[i]][1]+k);
    }
    if(ts==0)siz[x]=1;

}
void init()
{
    memset(fir,0,sizeof(fir));
    cnt=0;
    memset(du,0,sizeof(du));
}
int main()
{
    int T;
    T=read();
    while(T--)
    {
        init();
        n=read();
        int p,q;
        for(int i=1;i<n;i++)
        {
            p=read();q=read();
            add_e(p,q);add_e(q,p);
            du[p]++;du[q]++;
        }
        int ss=0;
        root=0;
        for(int i=1;i<=n;i++)
        {
            if(du[i]!=1)root=i;
            else ss++;
        }
        dfs1(root,0);
        if(n==2)cout<<"1\n";
        else cout<<dp[root][ss&1]<<"\n";
    }
}