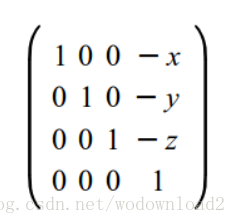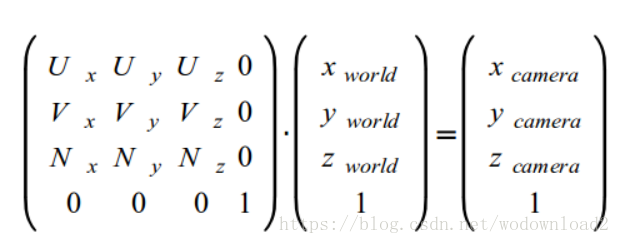OGL(教程13)——攝像機空間
原文地址:http://ogldev.atspace.co.uk/www/tutorial13/tutorial13.html
背景知識:
在前面的幾個章節中,我麼能看到兩種型別的變換。第一種型別的變換是改變位置(平移變換),方向變換(旋轉變換),大小(縮放)變換。這些變換允許我們把物體放在3D世界中的任一個位置。第二種型別的變換就是透視變換,這個是3D世界中的點透視到2D空間中去。一旦座標是2D世界中了,就很容易把他們對映到螢幕空間座標中去。
到目前所缺失謎題就是攝像機的位置。在之前的章節中,我們假設相機就是簡單的放在3D空間的原點位置。事實上,我們想自由的控制攝像機的位置,我們想把它放在3D空間的任意位置,然後把它看到的頂點對映到2D空間。這個會直觀的展示攝像機和螢幕上的物體。
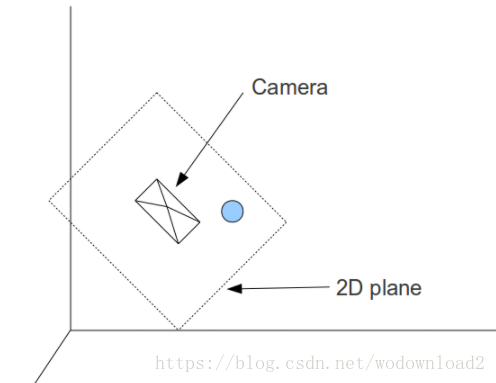
下圖我們可以看到攝像機的背面。這裡有一個虛擬的2D平面在它之前,然後這個球被對映到了平面上。由於我們是從攝像機看世界,所以看到的世界和攝像機的張角有關係。超出邊界的會被裁剪掉。把看到的四邊形對映到螢幕是我們的目標。
理論上來說,把攝像機之前的任何物體,通過變換都可以從3D對映到2D。但是,數學變換要很複雜,如前所見。如果把攝像機放在3D世界的原點,並且它是看著z軸方向,這個變換就容易的多了。比如,如果物體放在(0,0,5),攝像機在(0,0,1),朝向z軸方向。如果我們移動攝像機和物體,朝著原點方向移動一個單位,相對距離和朝向保持不變,只是攝像機放在了原點。如果用同樣的方式移動所有的物體,我們可以按照之前的方法渲染場景。
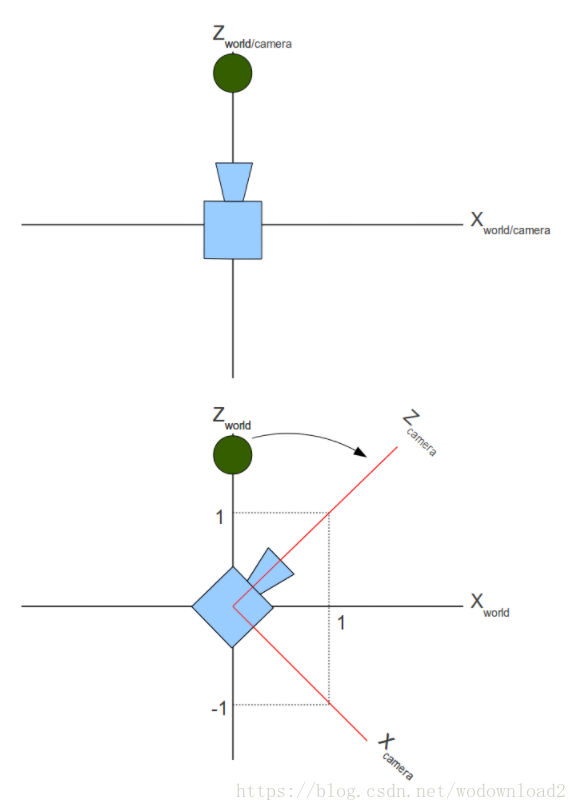
上面的例子很簡單,因為攝像機已經朝向z軸,並且是放在原點位置。但是如果攝像機的是看著其他方式呢?比如下圖:
攝像機有朝著z,然後順時針旋轉了45度。如你看到的,攝像機定義了自己的座標系統,和世界座標系一樣。所以事實上有兩個獨立的座標系統。其中一個叫做世界座標系,另外一個就是視口座標系。
綠色的球放在(0,y,z)世界座標內。而在攝像機空間此球則處在左邊位置,它有負的x和正的z。我們需要找到攝像機空間中這個球的位置。這樣我們就可以忘記世界空間,只使用相機空間。在相機空間,相機處在原點,朝著z軸看。哪些以攝像機定義的相對位置可以使用之前的公式進行渲染。
如果說攝像機順時針旋轉了45度,也就是說球逆時針旋轉了45度。物體的移動和攝像機的移動是相反的。所以通常,我們需要增加兩個新的變換,然後把他們插入到管線中。我們需要移動物體,保持它距離攝像機的距離和攝像機距離原點的距離相同。我們還需要移動物體,和攝像機的移動相反的方向移動。
移動攝像機很簡單。如果攝像機處在(x,y,z),那麼平移變換則為(-x,-y,-z)。這樣變換矩陣就為:
接下來一步是把攝像機轉換到某個目標,此目標是在世界空間。我們想找到新座標系統下的頂點的位置。所以問題實質為:我們如何把一個點從一個座標系統轉換到另外一個系統?
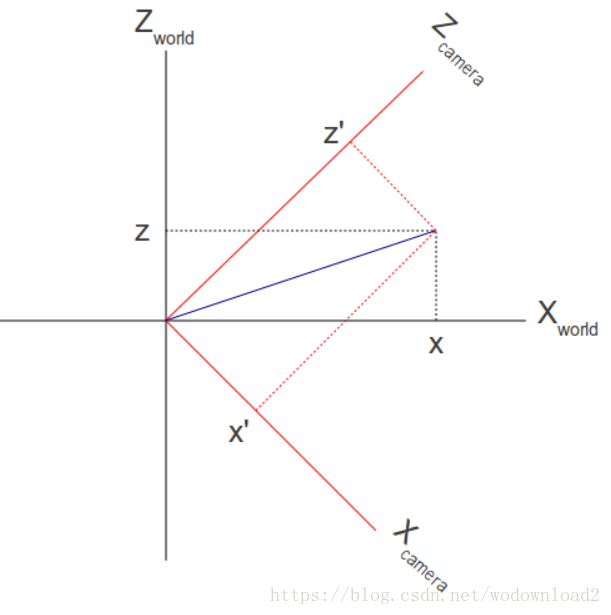
看上面的圖,我們的世界空間座標系為:(1,0,0),(0,1,0),(0,0,1)。線性無圖指的是,我們可以找不到xyz,使得x*(1,0,0)+y*(0,1,0)+z*(0,0,1)=(0,0,0)。從幾何術語來說 ,任意一個向量,和另外兩個向量構成的螢幕是垂直的。很容易得到上面的攝像機系統為(1,0,-1),(0,1,0),(1,0,1),經過標準化之後,我們得到(0.7071,0,-0.7071), (0,1,0) ,(0.7071,0,0.7071)。
下面的圖展示了兩個座標系統的軸資訊:
我們知道如何得到單位向量,它代表了相機的座標軸(而且是在世界空間內),而且我們知道世界空間的位置(x,y,z)。我麼所要找到的是向量(x’,y’,z’)。我們利用點乘的操作,稱之為標量透視。標量透視的結構是任意向量A和單位向量B。A在B上的投影。上面的例子中,我們將(x,y,z)和單位向量相乘得到的是X對應x’。同樣的方法y對應y’,z得到z’,(x’,y’,z’)就是(x,y,z)在攝像機空間的位置。
我們把這個知識用於解決攝像機的朝向問題。這個方法是uvn攝像機,它是定義攝像機朝向的一種方法。此方法的定義方式如下:
- N——攝像機到目標的向量。這個在3D中叫做朝向,這個向量和Z軸相關。
- V——如果是垂直站立的,這個向量就是頭朝向天空的向量。如果你寫的是一個飛機模擬器,那麼這個方向就是朝著地面的。此向量和Y軸相關。
- U——這個向量指向的是攝像機的右側,和X軸相關。
為了把世界座標系點轉換到攝像機空間(uvn向量),具體如下:
本節教程的程式碼中,全域性變數gWorld變為了gWVP。這個變化代表了一系列的變換。WVP代表了World-View-Position。
程式碼註釋:
本節,我們需要做些變換,然後把基礎的矩陣操作從Pipeline類中移動到Matrix4f類中。Pipeline告訴Matrix4f,如何初始化自己,然後連線一些矩陣建立最終的變換矩陣。
(pipelin.h:85)
struct {
Vector3f Pos;
Vector3f Target;
Vector3f Up;
} m_camera;
Pipeline類中包含了幾個方法用來儲存攝像機的引數。注意到指向攝像機右側的丟失了,變為了u。它是通過目標和向上向量叉乘得到。除此之外還有一個SetCamera方法,用來傳遞這些值。
(math3d.h:21)
Vector3f Vector3f::Cross(const Vector3f& v) const
{
const float _x = y * v.z - z * v.y;
const float _y = z * v.x - x * v.z;
const float _z = x * v.y - y * v.x;
return Vector3f(_x, _y, _z);
}
Vector3f有一個新的方法,叉乘的方法。兩個向量的叉乘,得到是一個垂直這兩個向量的向量。所有向量只有方向有意義,起點沒有意義。
(math3d.h:30)
Vector3f& Vector3f::Normalize()
{
const float Length = sqrtf(x * x + y * y + z * z);
x /= Length;
y /= Length;
z /= Length;
return *this;
}
為了得到uvn矩陣,我們需要把向量單位化,上面的函式就是單位化函式。
(math3d.cpp:84)
void Matrix4f::InitCameraTransform(const Vector3f& Target, const Vector3f& Up)
{
Vector3f N = Target;
N.Normalize();
Vector3f U = Up;
U = U.Cross(Target);
U.Normalize();
Vector3f V = N.Cross(U);
m[0][0] = U.x; m[0][1] = U.y; m[0][2] = U.z; m[0][3] = 0.0f;
m[1][0] = V.x; m[1][1] = V.y; m[1][2] = V.z; m[1][3] = 0.0f;
m[2][0] = N.x; m[2][1] = N.y; m[2][2] = N.z; m[2][3] = 0.0f;
m[3][0] = 0.0f; m[3][1] = 0.0f; m[3][2] = 0.0f; m[3][3] = 1.0f;
}
上面的函式得到的攝像機變換矩陣,供後面的管線類使用。uvn向量,在矩陣中用行展示。由於頂點位置是在右邊相乘。
(pipeline.cpp:22)
const Matrix4f* Pipeline::GetTrans()
{
Matrix4f ScaleTrans, RotateTrans, TranslationTrans, CameraTranslationTrans, CameraRotateTrans, PersProjTrans;
ScaleTrans.InitScaleTransform(m_scale.x, m_scale.y, m_scale.z);
RotateTrans.InitRotateTransform(m_rotateInfo.x, m_rotateInfo.y, m_rotateInfo.z);
TranslationTrans.InitTranslationTransform(m_worldPos.x, m_worldPos.y, m_worldPos.z);
CameraTranslationTrans.InitTranslationTransform(-m_camera.Pos.x, -m_camera.Pos.y, -m_camera.Pos.z);
CameraRotateTrans.InitCameraTransform(m_camera.Target, m_camera.Up);
PersProjTrans.InitPersProjTransform(m_persProj.FOV, m_persProj.Width, m_persProj.Height, m_persProj.zNear, m_persProj.zFar);
m_transformation = PersProjTrans * CameraRotateTrans * CameraTranslationTrans * TranslationTrans * RotateTrans * ScaleTrans;
return &m_transformation;
}