【6年人工智慧開發】簡述卷積神經網路(CNN)
在百度做了6年人工智慧方面的程式設計開發,也有很多這方面的經驗吧,從古至今,機器人一直承載著人類巨大的夢想。隨著各類感測器、語音互動、機器識別、SLAM等技術的蓬勃發展,機器人開始從科幻作品中走出,走進人們的生活。下面給大家簡述一下深度學習方面的卷積神經網路。
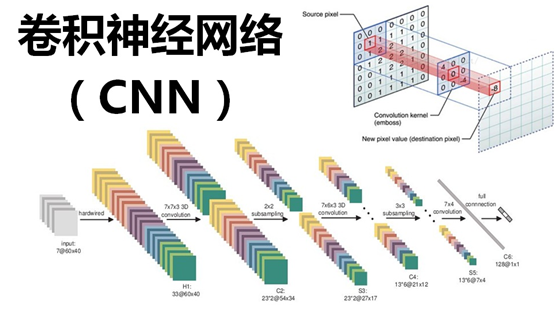
這幾年深度學習快速發展,在影象識別、語音識別、物體識別等各種場景上取得了巨大的成功,例如AlphaGo擊敗世界圍棋冠軍,iPhone X內建了人臉識別解鎖功能等等,很多AI產品在世界上引起了很大的轟動。在這場深度學習革命中,卷積神經網路(Convolutional Neural Networks,簡稱CNN)是推動這一切爆發的主力,在目前人工智慧的發展中有著非常重要的地位。
【問題來了】那什麼是卷積神經網路(CNN)呢?
1、小白一下,什麼是神經網路?
這裡的神經網路,也指人工神經網路(Artificial Neural Networks,簡稱ANNs),是一種模仿生物神經網路行為特徵的演算法數學模型,由神經元、節點與節點之間的連線(突觸)所構成,如下圖: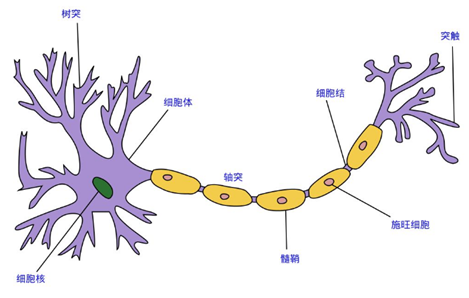
每個神經網路單元抽象出來的數學模型如下,也叫感知器,它接收多個輸入(x1,x2,x3...),產生一個輸出,這就好比是神經末梢感受各種外部環境的變化(外部刺激),然後產生電訊號,以便於轉導到神經細胞(又叫神經元)。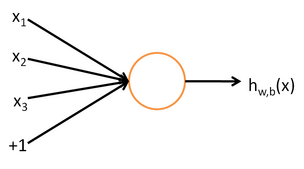
單個的感知器就構成了一個簡單的模型,但在現實世界中,實際的決策模型則要複雜得多,往往是由多個感知器組成的多層網路,如下圖所示,這也是經典的神經網路模型,由輸入層、隱含層、輸出層構成。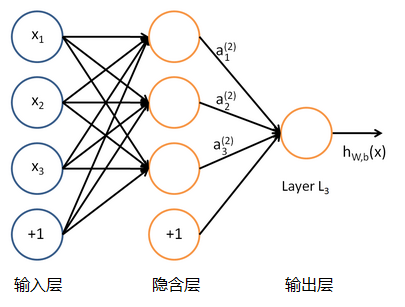
人工神經網路可以對映任意複雜的非線性關係,具有很強的魯棒性、記憶能力、自學習等能力,在分類、預測、模式識別等方面有著廣泛的應用。
2、重點來了,什麼是卷積神經網路?
卷積神經網路在影象識別中大放異彩,達到了前所未有的準確度,有著廣泛的應用。接下來將以影象識別為例子,來介紹卷積神經網路的原理。
(1)案例
假設給定一張圖(可能是字母X或者字母O),通過CNN即可識別出是X還是O,如下圖所示,那怎麼做到的呢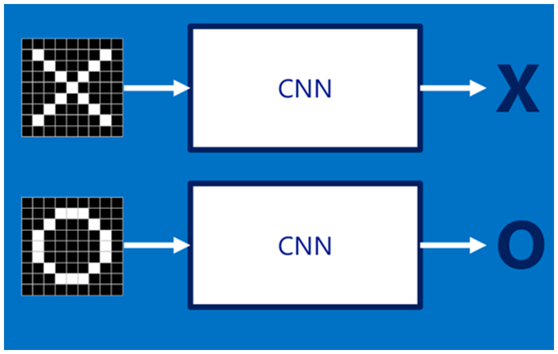
(2)影象輸入
如果採用經典的神經網路模型,則需要讀取整幅影象作為神經網路模型的輸入(即全連線的方式),當影象的尺寸越大時,其連線的引數將變得很多,從而導致計算量非常大。
而我們人類對外界的認知一般是從區域性到全域性,先對區域性有感知的認識,再逐步對全體有認知,這是人類的認識模式。在影象中的空間聯絡也是類似,區域性範圍內的畫素之間聯絡較為緊密,而距離較遠的畫素則相關性較弱。因而,每個神經元其實沒有必要對全域性影象進行感知,只需要對區域性進行感知,然後在更高層將區域性的資訊綜合起來就得到了全域性的資訊。這種模式就是卷積神經網路中降低引數數目的重要神器:區域性感受野。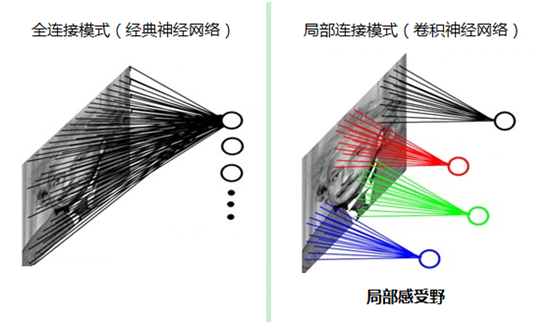
(3)提取特徵
如果字母X、字母O是固定不變的,那麼最簡單的方式就是影象之間的畫素一一比對就行,但在現實生活中,字型都有著各個形態上的變化(例如手寫文字識別),例如平移、縮放、旋轉、微變形等等,如下圖所示:
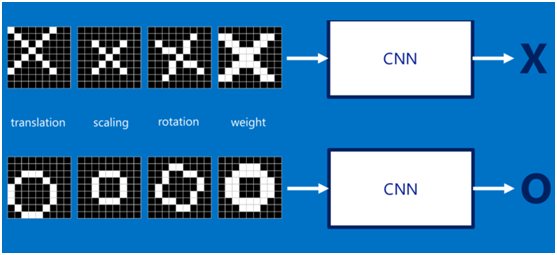
我們的目標是對於各種形態變化的X和O,都能通過CNN準確地識別出來,這就涉及到應該如何有效地提取特徵,作為識別的關鍵因子。
回想前面講到的“區域性感受野”模式,對於CNN來說,它是一小塊一小塊地來進行比對,在兩幅影象中大致相同的位置找到一些粗糙的特徵(小塊影象)進行匹配,相比起傳統的整幅圖逐一比對的方式,CNN的這種小塊匹配方式能夠更好的比較兩幅影象之間的相似性。如下圖:
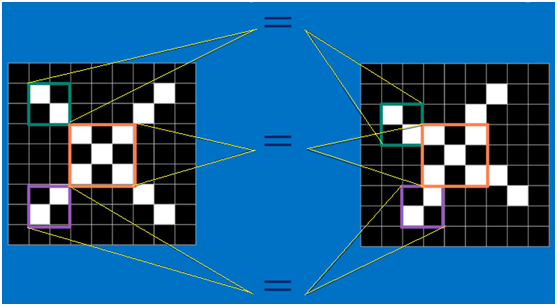
以字母X為例,可以提取出三個重要特徵(兩個交叉線、一個對角線),如下圖所示:
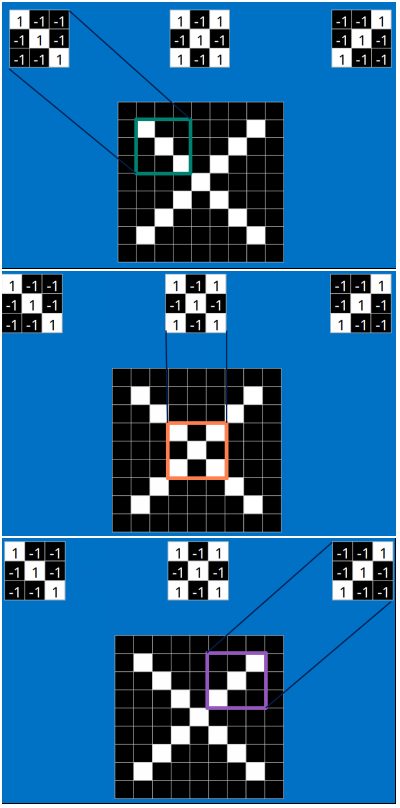
假如以畫素值"1"代表白色,畫素值"-1"代表黑色,則字母X的三個重要特徵如下:

那麼這些特徵又是怎麼進行匹配計算呢?(不要跟我說是畫素進行一一匹配的,汗!)
(4)卷積(Convolution)
這時就要請出今天的重要嘉賓:卷積。那什麼是卷積呢,不急,下面慢慢道來。
當給定一張新圖時,CNN並不能準確地知道這些特徵到底要匹配原圖的哪些部分,所以它會在原圖中把每一個可能的位置都進行嘗試,相當於把這個feature(特徵)變成了一個過濾器。這個用來匹配的過程就被稱為卷積操作,這也是卷積神經網路名字的由來。
卷積的操作如下圖所示:
是不是很像把毛巾沿著對角捲起來,下圖形象地說明了為什麼叫「卷」積

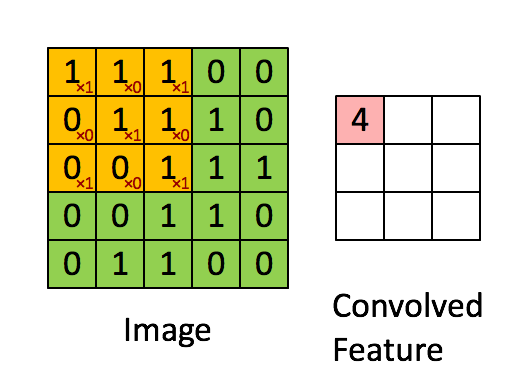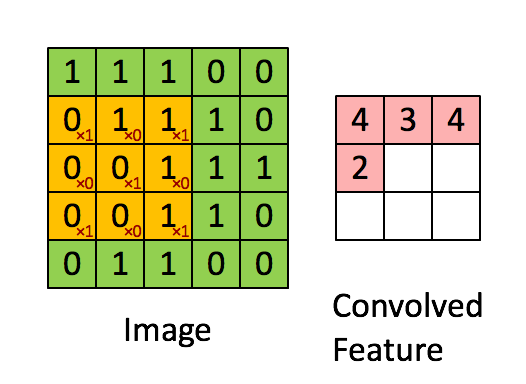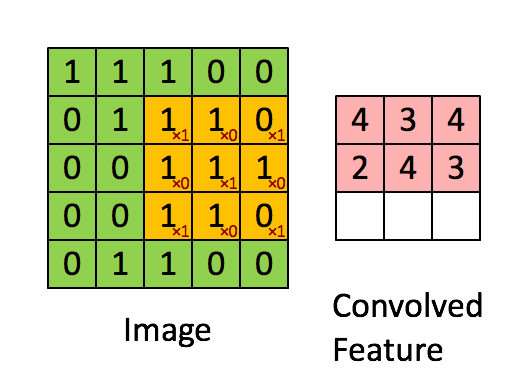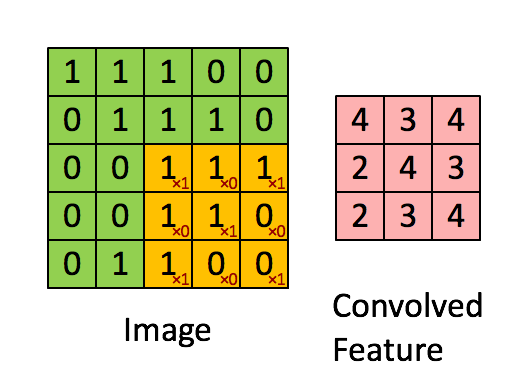
在本案例中,要計算一個feature(特徵)和其在原圖上對應的某一小塊的結果,只需將兩個小塊內對應位置的畫素值進行乘法運算,然後將整個小塊內乘法運算的結果累加起來,最後再除以小塊內畫素點總個數即可(注:也可不除以總個數的)。
如果兩個畫素點都是白色(值均為1),那麼1*1 = 1,如果均為黑色,那麼(-1)*(-1) = 1,也就是說,每一對能夠匹配上的畫素,其相乘結果為1。類似地,任何不匹配的畫素相乘結果為-1。具體過程如下(第一個、第二個……、最後一個畫素的匹配結果):
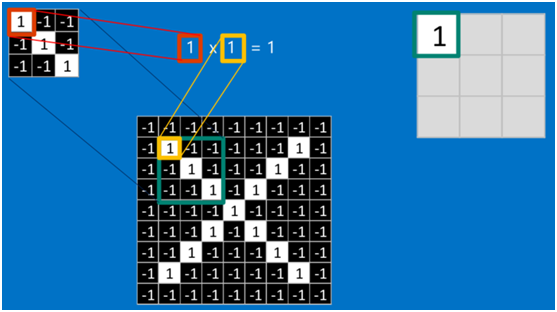
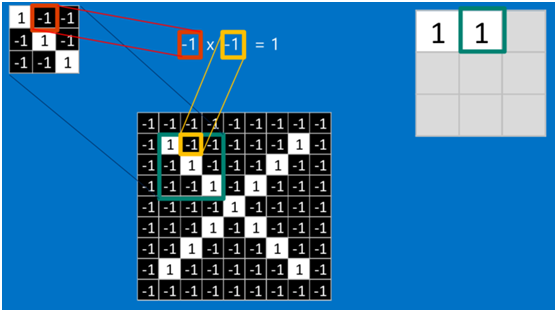
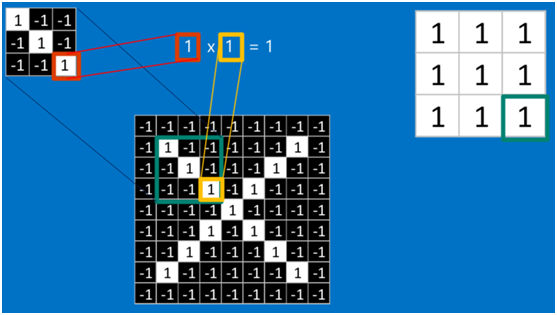
根據卷積的計算方式,第一塊特徵匹配後的卷積計算如下,結果為1
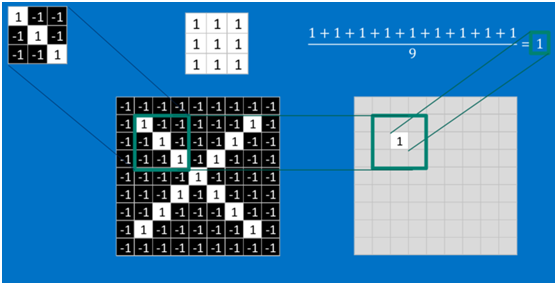
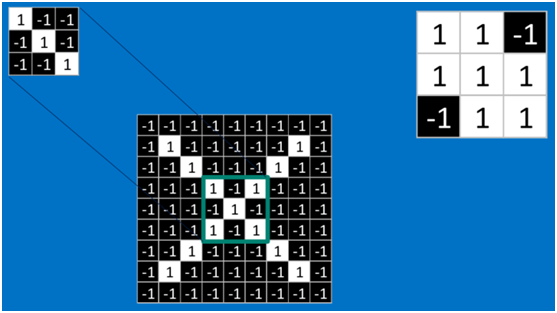
對於其它位置的匹配,也是類似(例如中間部分的匹配)
計算之後的卷積如下
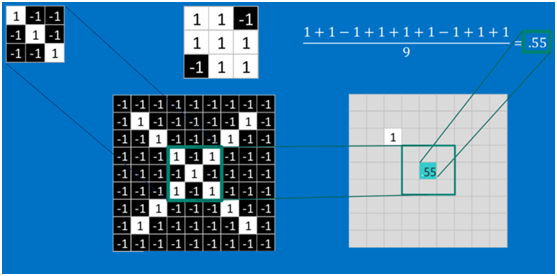
以此類推,對三個特徵影象不斷地重複著上述過程,通過每一個feature(特徵)的卷積操作,會得到一個新的二維陣列,稱之為feature map。其中的值,越接近1表示對應位置和feature的匹配越完整,越是接近-1,表示對應位置和feature的反面匹配越完整,而值接近0的表示對應位置沒有任何匹配或者說沒有什麼關聯。如下圖所示:

可以看出,當影象尺寸增大時,其內部的加法、乘法和除法操作的次數會增加得很快,每一個filter的大小和filter的數目呈線性增長。由於有這麼多因素的影響,很容易使得計算量變得相當龐大。
(5)池化(Pooling)
為了有效地減少計算量,CNN使用的另一個有效的工具被稱為“池化(Pooling)”。池化就是將輸入影象進行縮小,減少畫素資訊,只保留重要資訊。
池化的操作也很簡單,通常情況下,池化區域是2*2大小,然後按一定規則轉換成相應的值,例如取這個池化區域內的最大值(max-pooling)、平均值(mean-pooling)等,以這個值作為結果的畫素值。
下圖顯示了左上角2*2池化區域的max-pooling結果,取該區域的最大值max(0.77,-0.11,-0.11,1.00),作為池化後的結果,如下圖:
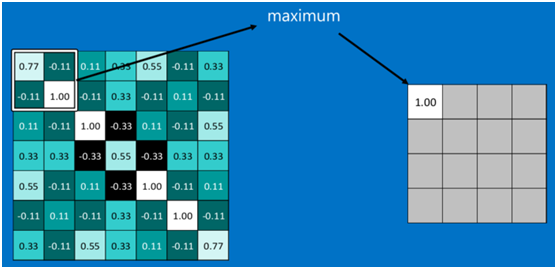
池化區域往左,第二小塊取大值max(0.11,0.33,-0.11,0.33),作為池化後的結果,如下圖:
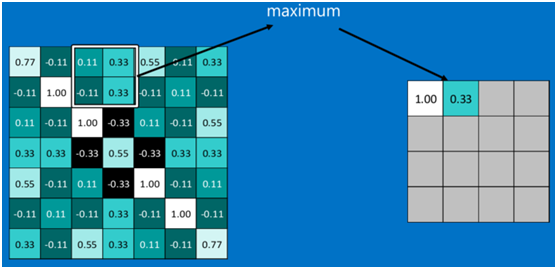
其它區域也是類似,取區域內的最大值作為池化後的結果,最後經過池化後,結果如下:
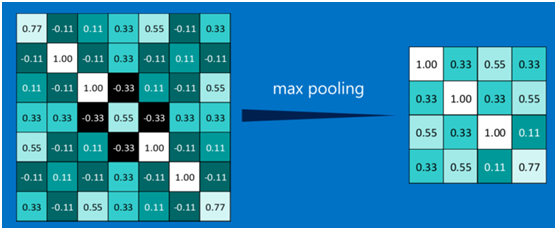
對所有的feature map執行同樣的操作,結果如下:

最大池化(max-pooling)保留了每一小塊內的最大值,也就是相當於保留了這一塊最佳的匹配結果(因為值越接近1表示匹配越好)。也就是說,它不會具體關注視窗內到底是哪一個地方匹配了,而只關注是不是有某個地方匹配上了。
通過加入池化層,影象縮小了,能很大程度上減少計算量,降低機器負載。
(6)啟用函式ReLU (Rectified Linear Units)
常用的啟用函式有sigmoid、tanh、relu等等,前兩者sigmoid/tanh比較常見於全連線層,後者ReLU常見於卷積層。
回顧一下前面講的感知機,感知機在接收到各個輸入,然後進行求和,再經過啟用函式後輸出。啟用函式的作用是用來加入非線性因素,把卷積層輸出結果做非線性對映。
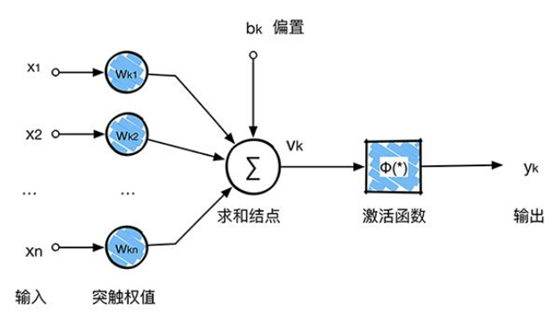
在卷積神經網路中,啟用函式一般使用ReLU(The Rectified Linear Unit,修正線性單元),它的特點是收斂快,求梯度簡單。計算公式也很簡單,max(0,T),即對於輸入的負值,輸出全為0,對於正值,則原樣輸出。
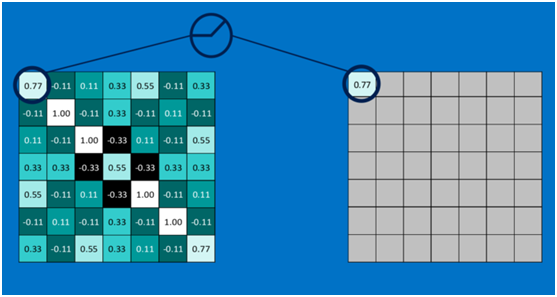
下面看一下本案例的ReLU啟用函式操作過程:
第一個值,取max(0,0.77),結果為0.77,如下圖
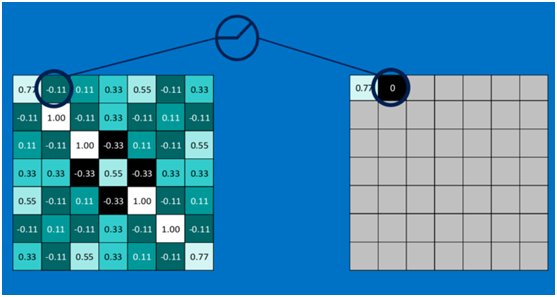
第二個值,取max(0,-0.11),結果為0,如下圖
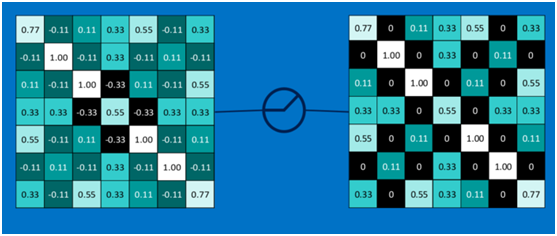
以此類推,經過ReLU啟用函式後,結果如下:
對所有的feature map執行ReLU啟用函式操作,結果如下:

(7)深度神經網路
通過將上面所提到的卷積、啟用函式、池化組合在一起,就變成下圖:
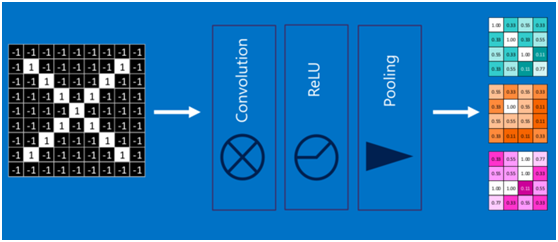
通過加大網路的深度,增加更多的層,就得到了深度神經網路,如下圖:
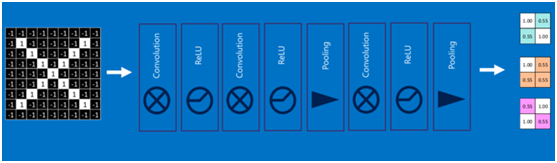
(8)全連線層(Fully connected layers)
全連線層在整個卷積神經網路中起到“分類器”的作用,即通過卷積、啟用函式、池化等深度網路後,再經過全連線層對結果進行識別分類。
首先將經過卷積、啟用函式、池化的深度網路後的結果串起來,如下圖所示:
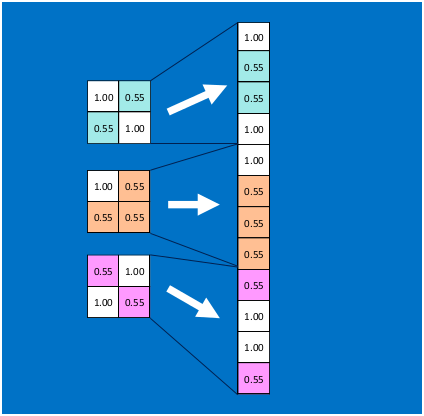
由於神經網路是屬於監督學習,在模型訓練時,根據訓練樣本對模型進行訓練,從而得到全連線層的權重(如預測字母X的所有連線的權重)

在利用該模型進行結果識別時,根據剛才提到的模型訓練得出來的權重,以及經過前面的卷積、啟用函式、池化等深度網路計算出來的結果,進行加權求和,得到各個結果的預測值,然後取值最大的作為識別的結果(如下圖,最後計算出來字母X的識別值為0.92,字母O的識別值為0.51,則結果判定為X)
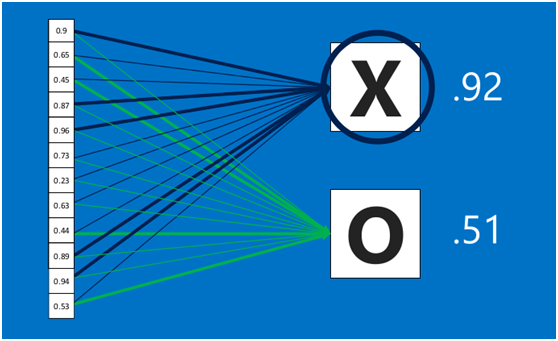
上述這個過程定義的操作為”全連線層“(Fully connected layers),全連線層也可以有多個,如下圖:
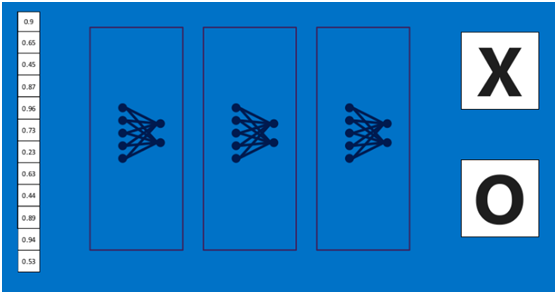
(9)卷積神經網路(Convolutional Neural Networks)
將以上所有結果串起來後,就形成了一個“卷積神經網路”(CNN)結構,如下圖所示:
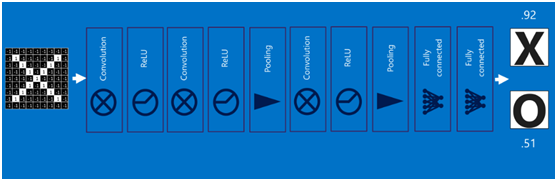
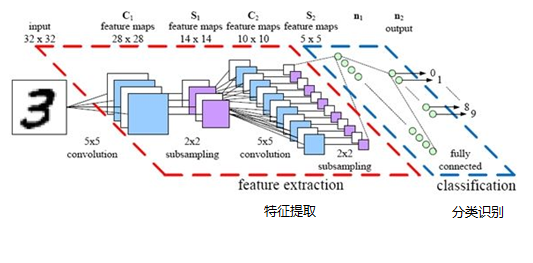
最後,再回顧總結一下,卷積神經網路主要由兩部分組成,一部分是特徵提取(卷積、啟用函式、池化),另一部分是分類識別(全連線層),下圖便是著名的手寫文字識別卷積神經網路結構圖:(原文出處:https://blog.csdn.net/Stephen_shijun/article/details/83109282)