神經網路概述

神經元模型

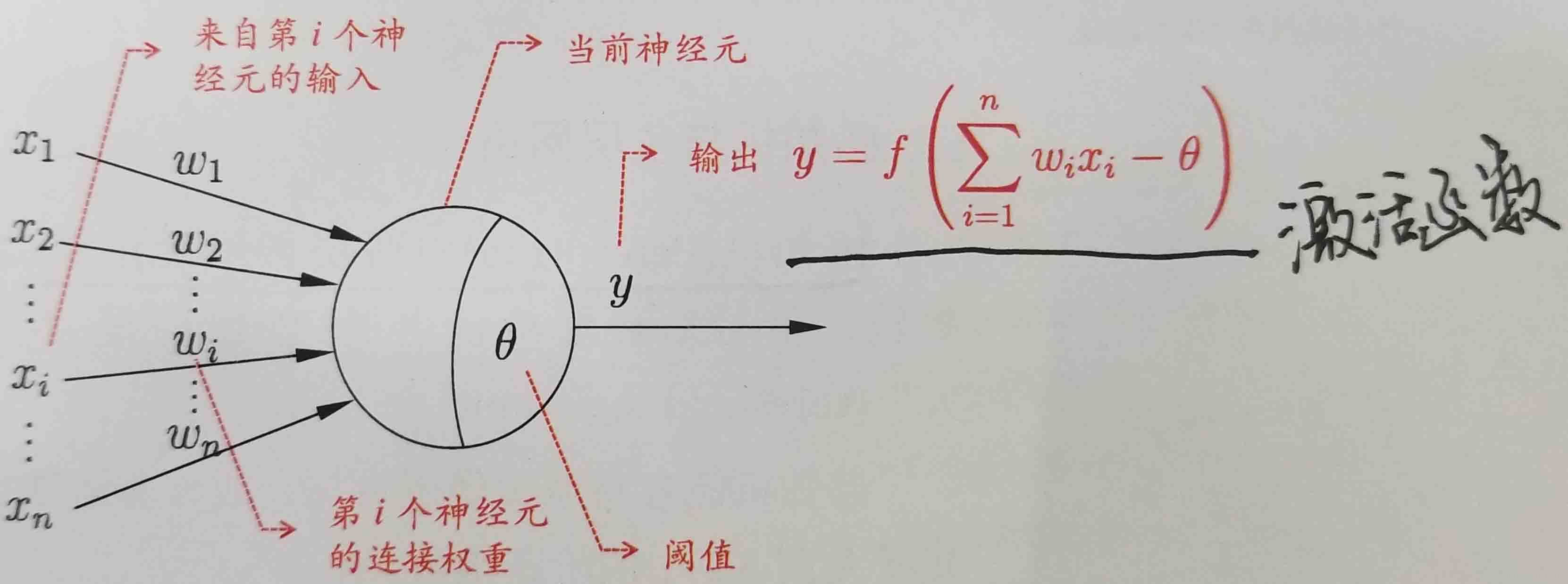
以上就是經典的“M-P神經元模型”。在這個模型中，神經元接收來自n個其他神經元傳遞過來的輸入訊號，這些輸入訊號通過帶權重的連線進行傳遞，神經元接收到的總輸入值將於神經元的閾值進行比較，然後通過“啟用函式”處理以產生神經元的輸出。

感知機

感知機（Perceptron）是由兩層神經元組成，輸入層接收外界輸出訊號後傳遞給輸出層，輸出層是M-P神經元，也稱為“閾值邏輯單元”。

感知機能夠很容易的實現邏輯與、或、非運算，但是由於其只有輸出層神經元進行啟用函式處理，即只擁有一層功能神經元，所以學習能力非常有限。此時就產生了多層感知機（MLP）來處理這些更加複雜的運算。

對於以上的感知機，我們可以建立模型：

f(x)=act(θT+b)
其中啟用函式 act 可以使用{sign, sigmoid, tanh}之一，個人感覺這種建模方式就是將每個神經元的輸入作為笛卡爾座標系中的x軸的值，對應的輸出值作為y軸上的值，通過這些已知的訓練集合中的值來進行擬合，根據訓練集在座標系中的分佈特徵來選擇不同的啟用函式，也即是擬合方式的不同，就比如下面的線性迴歸，邏輯迴歸以及softmax迴歸。

• 啟用函式使用符號函式 sign ，可求解損失函式最小化問題，通過梯度下降確定引數
• 啟用函式若使用一次多項式進行擬合，就成為了線性迴歸，但是一般不用此種迴歸方法來擬合。
• 啟用函式使用 sigmoid （或者 tanh ），即解決的問題為二分問題，則分類器事實上成為Logistic Regression，可通過梯度上升極大化似然函式，或者梯度下降極小化損失函式，來確定引數。
• 如果需要多分類，則事實上成為Softmax Regression。
• 如要需要分離超平面恰好位於正例和負例的正中央，則成為支援向量機（SVM）。

多層感知機

感知機存在的問題是，對線性可分資料工作良好，如果設定迭代次數上限，則也能一定程度上處理近似線性可分資料。但是對於非線性可分的資料，比如最簡單的異或問題，感知器就無能為力了。這時候就需要引入多層感知器這個大殺器。

多層感知器的思路是，儘管原始資料是非線性可分的，但是可以通過某種方法將其對映到一個線性可分的高維空間中，從而使用線性分類器完成分類。下面卷積神經網路概述神經網路的大體結構圖中，從X到O這幾層，正展示了多層感知器的一個典型結構，即輸入層-隱層-輸出層。

輸入層-隱層
是一個全連線的網路，即每個輸入節點都連線到所有的隱層節點上。更詳細地說，可以把輸入層視為一個向量 x ，而隱層節點 j有一個權值向量θj以及偏置bj，啟用函式使用 sigmoid 或 tanh ，那麼這個隱層節點的輸出應該是

fj(x)=act(θTjx+bj)
也就是每個隱層節點都相當於一個感知器。每個隱層節點產生一個輸出，那麼隱層所有節點的輸出就成為一個向量，即
f(x)=act(Θx+b)
若輸入層有m個節點，隱層有n個節點，那麼Θ=[θT]為n×m的矩陣，x為長為m的向量，b為長為n的向量，啟用函式作用在向量的每個分量上， f(x)返回一個向量。

隱層-輸出層
可以視為級聯在隱層上的一個感知器。若為二分類，則常用Logistic Regression；若為多分類，則常用Softmax Regression。

解決非線性最優問題的常見演算法

為討論下面幾種演算法，採用最簡單的線性迴歸作為例子。相關的引數如下（一般機器學習中都相關問題都是採用下列的引數）：
n：訓練集合的特徵數量，例如房價預測中的房子的大小和臥室的數量
m：訓練樣本的數量
x：輸入變數/特徵
y：輸出變數/特徵
(x,y)：訓練樣例
ith：訓練樣例的組數，表示為：(x(i),y(i))
h(x)：擬合函式
J(x)：損失函式

（此處注意上面推出的這個迭代式，下面要與邏輯迴歸中推出的迭代式進行比較）
（3）隨機梯度下降法（stochastic gradient descent，SGD）
SGD是最速梯度下降法的變種。
使用最速梯度下降法，將進行N次迭代，直到目標函式收斂，或者到達某個既定的收斂界限。每次迭代都將對m個樣本進行計算，計算量大。
為了簡便計算，SGD每次迭代僅對一個樣本計算梯度，直到收斂。虛擬碼如下（以下僅為一個loop，實際上可以有多個這樣的loop，直到收斂）：

1、由於SGD每次迭代只使用一個訓練樣本，因此這種方法也可用作online learning。
2、每次只使用一個樣本迭代，若遇上噪聲則容易陷入區域性最優解。
（4）牛頓法

（5）高斯牛頓法
以上兩種方法的詳細數學推導http://blog.csdn.net/jinshengtao/article/details/51615162

線性迴歸和邏輯迴歸

線性迴歸的一個具體實現可以從上面解決非線性最優問題的常見演算法的例子裡學習，下面首先給出一個對於線性迴歸的一個可能的解釋。

Probabilistic Interpretation

區域性加權迴歸（Locally weight regression，Loess/Lowess）

邏輯迴歸（Logistic Regression）

誤差逆傳播（BP）演算法

通過以上的介紹我們弄清楚了神經網路的結構，常見的神經網路有多層前饋網路（每層神經元與下一層神經元全連線，神經元之間不存在同層連線，也不存在跨層連線），下面就是介紹訓練類似的多層網路（即估計權重和閾值這些引數）的方法了。對於一般的問題，可以通過求解損失函式極小化問題來進行引數估計。但是對於多層感知器中的隱層，因為無法直接得到其輸出值，當然不能夠直接使用到其損失了。這時，就需要將損失從頂層反向傳播（Back Propagate）到隱層，來完成引數估計的目標。

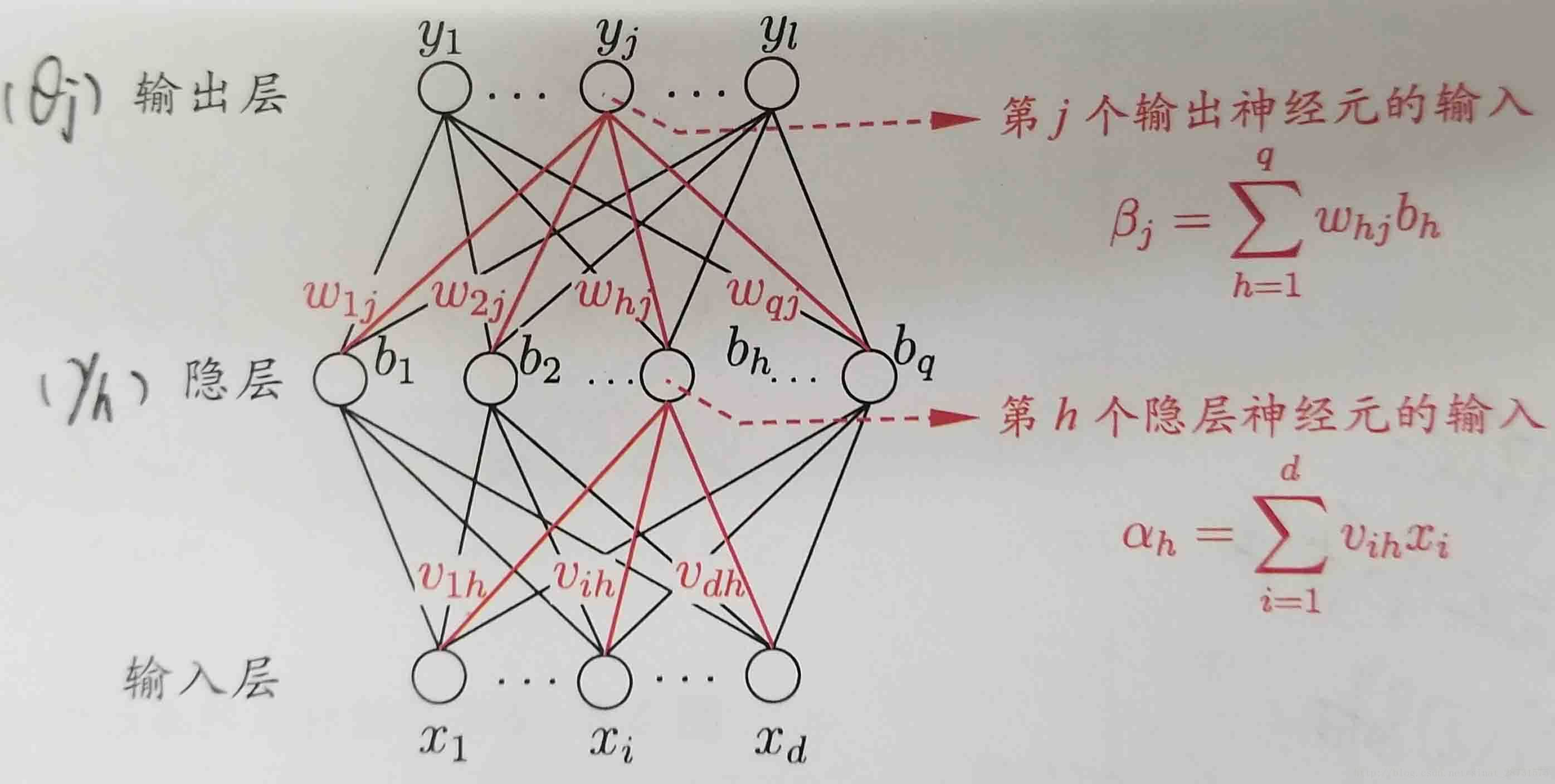
首先，我們給出下面的BP網路（用BP演算法訓練的多層前饋神經網路）：

給定訓練集D=(x1,y1),(x2,y2),……,(xm,ym),xi∈Rd,yi∈Rl，即輸入示例由d個屬性描述，輸出l維實值向量。為了便於討論，上圖給出了一個擁有d個神經元、l個輸出神經元、q個隱層神經元的多層前饋網路結構，其中輸出層第j個神經元的閾值用θj表示，隱層第h個神經元的閾值用γh表示。輸出層第i個神經元與隱層第h個神經元之間的連線權為νih，隱層第h個神經元與輸出層第j個神經元之間的連線權為ωhj。記隱層第h個神經元接收到的輸入為αh=∑i=1dνihxi,輸出層第j個神經元接收到的輸入為βj=∑qh=1ωhjbh，其中