\(\hspace{2em}\)關於判斷函式的單調性問題，教材上所舉例子是從數的角度求解導函式的正負，從而判斷原函式的單調性，所以學生就依葫蘆畫瓢，碰到這類問題都這樣做，但是他會發現在高三中的大多這類題目都不能，這當碰到不能從數的角度求解的題目時思路自然會受阻而放棄，其實只需要老師做引導，如果從數的角度不能突破，可以考慮從形的角度入手分析，這類題目反倒會順利求解。

一、用導函式的影象判斷原函式的單調性

【例1】已知函式\(f(x)=2x^3+ax^2+bx+1\)的導函式為\(f'(x)\)，若函式\(y=f'(x)\)的對稱軸是\(x=-\cfrac{1}{2}\)，且\(f'(1)=0\)

(1).求\(a，b\)的值。

(2).判斷函式的單調性，並求函式的極值。

【分析】(1)通過導函式方程和二次函式對稱軸方程建立方程組，即可解得a、b，

(2)數字係數的三次多項式函式求極值，用常規的思路和步驟求解即可。

【解答】(1)由於\(f'(x)=6x^2+2ax+b\)，且對稱軸為\(x=-\cfrac{1}{2}\)，

則有\(-\cfrac{a}{6}=-\cfrac{1}{2}\)，則\(a=3\)，

又由於\(f'(1)=0\)，則\(6+2a+b=0\)，解得\(b=-12\)，

所以\(a=3，b=-12\)。

(2)因為\(f(x)=2x^3+3x^2-12x+1\)，\(f'(x)=6x^2+6x-12=6(x^2+x-2)\)

輔助影象

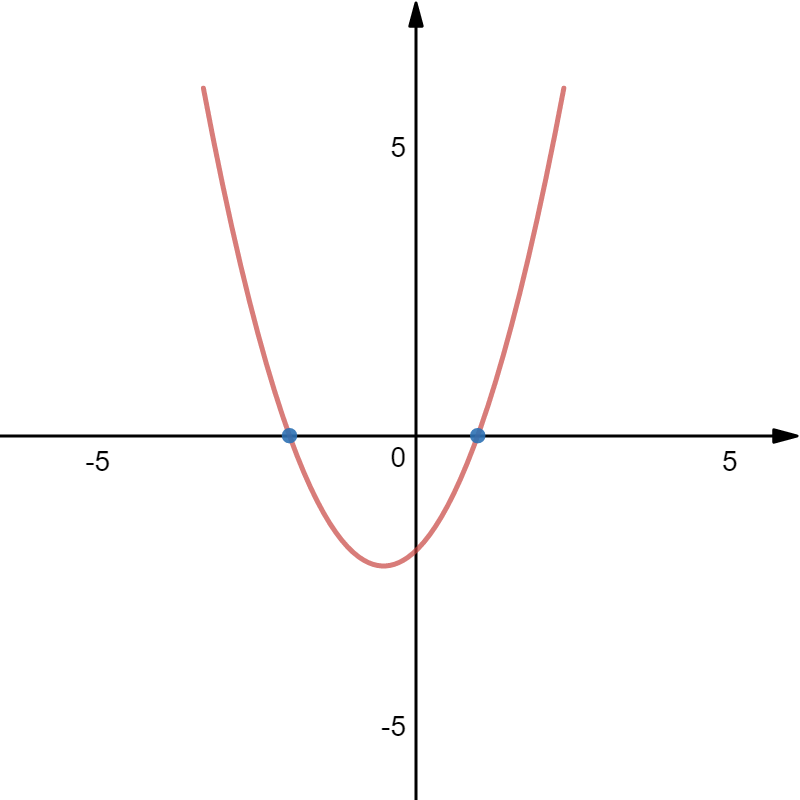
常規的解法這樣寫道：
令\(f'(x)≥0\)，即\(x^2+x-2≥0\)，解得\(x≥1\)或\(x≤-2\)，

令\(f'(x) ≤0\)，即\(x^2+x-2 ≤0\)，解得$ -2≤x ≤1$，

有了輔助影象後，我們這些寫：

當\(x< -2\)時，\(f'(x)>0\)，\(f(x)\)單調遞增；

當\(-2<x<1\)時，\(f'(x)<0\)，\(f(x)\)單調遞減；

當\(x>1\)時，\(f'(x)>0\)，\(f(x)\)單調遞增；

然後做總結：

所以函式\(f(x)\)在\((-2，1)\)上單調遞減，在\((-\infty，-2)\)

當\(x=-2\)時，\(f(x)\)取得極大值，為\(f(-2)=21\)，

當\(x=1\)時，\(f(x)\)取得極小值，為\(f(1)=-6\)。

二、用導函式的分子影象判斷原函式的單調性

已知函式\(f(x)=x^2+2mlnx-(m+4)x+lnm+2\)．（Ⅱ）當\(m＞0\)時，試討論函式\(f(x)\)的單調性；

【分析】（Ⅱ）藉助導函式的分子函式的動態影象，即可判斷導函式的正負，從而判斷原函式的單調性。

【解答】輔助影象

（Ⅱ）\(f'(x)=2x+\cfrac{2m}{x}-(m+4)=\cfrac{2x^2-(m+4)x+2m}{x}=\cfrac{(x-2)(2x-m)}{x}\)，

令\(f'(x)=0\)，得到\(x=2\)或\(x=\cfrac{m}{2}>0\)，只需要藉助分子函式的影象，即可判斷導函式的正負，

當\(0<\cfrac{m}{2}<2\)時，即\(0<m<4\)時， \(x\in (0，\cfrac{m}{2})\)時，\(f'(x)>0\)，\(f(x)\)單調遞增，

\(x\in (\cfrac{m}{2}，2)\)時，\(f'(x)<0\)，\(f(x)\)單調遞減，\(x\in (2，+\infty)\)時，\(f'(x)>0\)，\(f(x)\)單調遞增，

當\(\cfrac{m}{2}=2\)時，即\(m=4\)時，此時\(f'(x)\ge 0\)恆成立，

當且僅當\(x=2\)時取得等號，故\(f(x)\)在\((0，+\infty)\)上單調遞增，

當\(\cfrac{m}{2}>2\)時，即\(m>4\)時， \(x\in (0，2)\)時，\(f'(x)>0\)，\(f(x)\)單調遞增，

\(x\in (2，\cfrac{m}{2})\)時，\(f'(x)<0\)，\(f(x)\)單調遞減， \(x\in (\cfrac{m}{2}，+\infty)\)時，\(f'(x)>0\)，\(f(x)\)單調遞增，

綜上所述，

當\(0<m<4\)時， \(x\in (0，\cfrac{m}{2})\)時，\(f(x)\)單調遞增，

\(x\in (\cfrac{m}{2}，2)\)時，\(f(x)\)單調遞減，

\(x\in (2，+\infty)\)時，\(f(x)\)單調遞增，

當\(m=4\)時，\(f(x)\)在\((0，+\infty)\)上單調遞增，

當\(m>4\)時， \(x\in (0，2)\)時，\(f(x)\)單調遞增，

\(x\in (2，\cfrac{m}{2})\)時，\(f(x)\)單調遞減，

\(x\in (\cfrac{m}{2}，+\infty)\)時，\(f(x)\)單調遞增，

三、用導函式中的一部分函式影象判斷原函式的單調性

已知函式\(f(x)=x^2+(m+2)x+1(m為常數)\)．（Ⅰ）討論函式\(g(x)=e^xf(x)\)的單調性；

【分析】（Ⅰ）求導後藉助導函式的部分函式\(y=(x+1)(x+m+3)\)的影象，

利用兩根的大小關係分類討論，可以輕鬆判斷其單調性；

【解答】（Ⅰ）\(g(x)=e^x[x^2+(m+2)x+1]\)，定義域為\(R\)，

則\(g'(x)=e^x\cdot [x^2+(m+2)x+1]+e^x\cdot (2x+m+2)\)

\(=e^x[x^2+(m+4)x+m+3]=e^x(x+1)[x+(m+3)]\)

令\(g'(x)=0\)，得到\(x=-1\)或\(x=-(m+3)\)，由於\(e^x>0\)恆成立，

故藉助開口向上的二次函式\(y=(x+1)[x+(m+3)]\)的影象求解如下：

①當\(-(m+3)<-1\)時，即\(m>-2\)時，

\(x\in (-\infty，-m-3)\)時，\(g'(x)>0\)，\(g(x)\)單調遞增，

\(x\in (-m-3，-1)\)時，\(g'(x)<0\)，\(g(x)\)單調遞減，

\(x\in (-1，+\infty)\)時，\(g'(x)>0\)，\(g(x)\)單調遞增，

②當\(-(m+3)=-1\)時，即\(m=-2\)時，\(g'(x)\ge 0\)恆成立，

當且僅當\(x=-1\)時取得等號，故\(g(x)\)在R上單調遞增；

③當\(-(m+3)>-1\)時，即\(m<-2\)時，

\(x\in (-\infty，-1)\)時，\(g'(x)>0\)，\(g(x)\)單調遞增，

\(x\in (-1，-m-3)\)時，\(g'(x)<0\)，\(g(x)\)單調遞減，

\(x\in (-m-3，+\infty)\)時，\(g'(x)>0\)，\(g(x)\)單調遞增，

綜上所述：

當\(m<-2\)時，函式\(g(x)\)的單增區間為\((-\infty，-1)\)和\((-m-3，+\infty)\)，單減區間為$ (-1，-m-3)$;

當\(m=-2\)時，函式\(g(x)\)只有單增區間為\((-\infty，+\infty)\)；

當\(m>-2\)時，函式\(g(x)\)的單增區間為\((-\infty，-m-3)\)和\((-1，+\infty)\)，單減區間為$ (-m-3，-1)$;

四、用導函式的幾個因子函式的影象和符號法則判斷導函式的正負

已知函式\(f(x)=(x-2)e^x+a(x-1)^2\)．討論\(f(x)\)的單調性．

【分析】利用導函式分解因式後的兩個因式函式的影象和符號法則判斷導函式的正負，

從而判斷原函式的單調性。

【解答】定義域為\(R\)，\(f'(x)=1\cdot e^x+(x-2)\cdot e^x+2a(x-1)=e^x(x-1)+2a(x-1)=(x-1)(e^x+2a)\)，

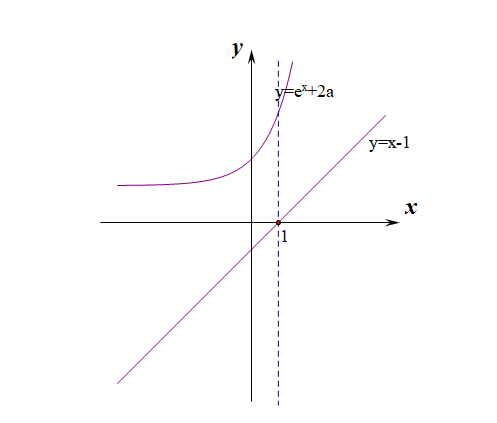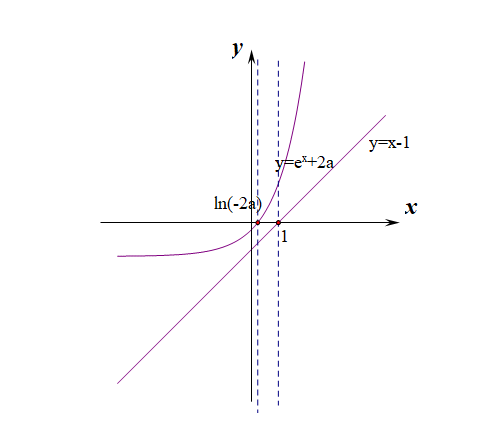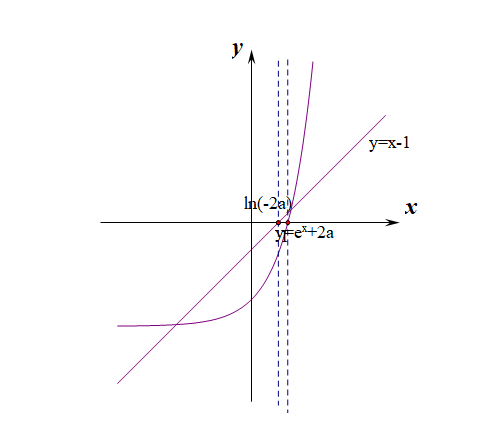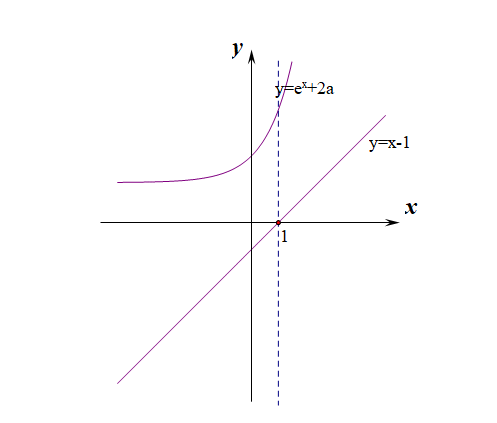
在同一個座標系中做出函式\(y=x-1\)(定圖)和函式\(y=e^x+2a\)(動圖)的影象，

根據動圖\(y=e^x+2a\)是否與\(x\)軸有交點分類討論如下：

①當\(2a\ge 0\)時，即\(a\ge 0\)時，恆有\(e^x+2a>0\)，

當\(x\in (-\infty，1)\)上時，\(x-1<0\) ，則\(f'(x)=(e^x+2a)(x-1)<0\)，故\(f(x)\)單調遞減，

當\(x\in (1，+\infty)\)上時，\(x-1>0\) ，則\(f'(x)=(e^x+2a)(x-1)>0\)，故\(f(x)\)單調遞增，

當\(2a<0\)時，即\(a<0\)時，\(y=e^x+2a\)與\(x\)軸有交點，令\(e^x+2a=0\)，解得\(x=ln(-2a)\)，

然後針對\(ln(-2a)\)與\(1\)的大小關係繼續細分如下

②當\(ln(-2a)<1\)時，即\(-\cfrac{e}{2}<a<0\)時，

當\(x\in(-\infty，ln(-2a))\)時，\(e^x+2a<0\)，\(x-1<0\)，則\(f'(x)>0\)，\(f(x)\)單調遞增；

當\(x\in(ln(-2a)，1)\)時，\(e^x+2a>0\)，\(x-1<0\)，則\(f'(x)<0\)，\(f(x)\)單調遞減；

當\(x\in(1，+\infty)\)時，\(e^x+2a>0\)，\(x-1>0\)，則\(f'(x)>0\)，\(f(x)\)單調遞增；

③當\(ln(-2a)=1\)時，即\(a=-\cfrac{e}{2}\)時，

當\(x\in(-\infty，1)\)時，\(e^x+2a<0\)，\(x-1<0\)，則\(f'(x)>0\)，\(f(x)\)單調遞增；

當\(x\in(1，+\infty)\)時，\(e^x+2a>0\)，\(x-1>0\)，則\(f'(x)>0\)，\(f(x)\)單調遞增；

即\(x\in (-\infty，+\infty)\)時，恆有\(f'(x)\ge 0\)，當且僅當\(x=1\)時取到等號，故\(f(x)\)單調遞增；

④當\(ln(-2a)>1\)時，即\(a<-\cfrac{e}{2}\)時，

當\(x\in(-\infty，1)\)時，\(e^x+2a<0\)，\(x-1<0\)，則\(f'(x)>0\)，\(f(x)\)單調遞增；

當\(x\in(1，ln(-2a))\)時，\(e^x+2a<0\)，\(x-1>0\)，則\(f'(x)<0\)，\(f(x)\)單調遞減；

當\(x\in(ln(-2a)，+\infty)\)時，\(e^x+2a>0\)，\(x-1>0\)，則\(f'(x)>0\)，\(f(x)\)單調遞增；

綜上所述，

當\(a<-\cfrac{e}{2}\)時，單增區間為\((-\infty，1)\)和\((ln(-2a)，+\infty)\)，單減區間為\((1，ln(-2a))\)；

當\(a=-\cfrac{e}{2}\)時，只有單增區間為\((-\infty，+\infty)\)；

當\(-\cfrac{e}{2}<a<0\)時，單增區間為\((-\infty，ln(-2a))\)和\((1，+\infty)\)，單減區間為\((ln(-2a)，1)\)；

當\(a\ge 0\)時，單減區間為\((-\infty，1)\)，單增區間為\((1，+\infty)\)；

【點評】由於教材上所舉例子是從數的角度求解導函式的正負，從而判斷原函式的單調性，

故許多學生碰到這個題目時思路會受阻，需要老師做引導，如果從數的角度不能突破，可以考慮從形的角度入手分析。

五、用二階導判斷一階導的正負

設函式\(f(x)=\cfrac{1}{2}{x^2}+aln(1+x)\)．（Ⅱ）若\(a=1\)，證明：當\(x＞0\)時，\(f(x)＜e^x-1\)．

【分析】（Ⅱ）先轉化為恆成立求最大值問題，先求一階導，此時不好判斷其正負，再求二階導，

由二階導的正負判斷一階導的增減性，進而知道一階導的正負，從而知道原函式的單調性。

【解答】（Ⅱ）當\(a=1\)時，\(f(x)=\cfrac{1}{2}{x^2}+ln(x+1)\)，欲證明\(x >0\) 時，\(f(x)<e^x-1\)，

即證明x>0時，\(\cfrac{1}{2}{x^2}+ln(x+1)-e^x+1<0\)恆成立。

令\(g(x)=\cfrac{1}{2}{x^2}+ln(x+1)-e^x+1\)，只需要證明\(g(x)_{max}<0\)即可。

\(g'(x)=x+\cfrac{1}{x+1}-e^x\)，令\(h(x)=x+\cfrac{1}{x+1}-e^x\)，

則\(h'(x)=1-e^x-\cfrac{1}{(1+x)^2}\)，當\(x>0\)時，\(h'(x)<0\)恆成立，

故函式\(g'(x)\)單調遞減，則有\(g'(x)<g'(0)=0\)，即有\(x >0\)時，\(g'(x)<0\)恆成立，

則\(x>0\)時，函式\(g(x)\)單調遞減，即有\(g(x)<g(0)=0\)恆成立，

即證明了\(x>0\)時，\(f(x)<e^x-1\)。

（Ⅱ）用導數證明不等式時，有一個很常用的思路是作差構造新函式，轉而求新函式的最值或最值的極限大於小於0。

還有一個常用思路是連求兩次導數，用二階導的正負先判斷一階導的增減，再利用一階導的增減在端點處的值再判斷一階導的正負，從而知道原函式的增減性。

六、含有\(e^x\)和\(lnx\)的導函式尋找分界點判斷導函式的正負

已知函式\(f(x)=e^x-ax-1(a∈R)\)，\(g(x)=lnx\)．（I）若不等式\(f(x)≥g(x)\)對任意的\(x∈(0，+\infty)\)恆成立，求實數a的取值範圍；

【解答】（I）由題目可知，\(e^x-ax-1\ge lnx\)對任意的\(x∈(0，+\infty)\)恆成立，

分離引數得到，\(a\leq \cfrac{e^x-1-lnx}{x}(x>0)\)；

令\(h(x)= \cfrac{e^x-1-lnx}{x}\)，需要求\(h(x)_{min}\)，

\(h'(x)=\cfrac{(e^x-\frac{1}{x})\cdot x-(e^x-1-lnx)\cdot 1}{x^2}\)

\(=\cfrac{xe^x-1-e^x+1+lnx}{x^2}\)

\(=\cfrac{(x-1)e^x+lnx}{x^2}\)

觀察分子的結構，可以發現兩部分\((x-1)e^x\)和\(lnx\)的零點都是\(x=1\)，故有

當\(x\in(0，1)\)時，\(x-1<0\)，\(lnx<0\)，則\(h'(x)<0\)，\(h(x)\)單調遞減；

當\(x\in(1，+\infty)\)時，\(x-1>0\)，\(lnx>0\)，則\(h'(x)>0\)，\(h(x)\)單調遞增；

故\(h(x)_{min}=h(1)=e-1\)，

即\(a\leq e-1\).