在白書上學到的有趣的知識。

單峰函式

即 先嚴格遞增再嚴格遞減 或 先遞減再遞增的函式

三分法：

取區間[L,R]兩個三分點m1,m2.
比較兩處的函式值，縮小範圍，繼續三分直到找出優解。
如下圖所示：

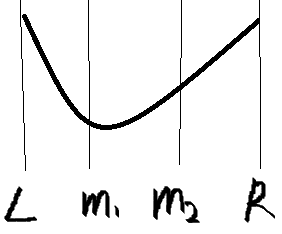
這是一個下凸的函式，我們要找最小值
很明顯m1的函式值要比m2小
這時我們就可以保證最小值在[L,m2]處取到。
繼續遞迴下去，就可找到滿意的解。
同理，上凸也如此。

讓我們看一道例題：

白書P164:
已知n條二次曲線Si，告訴二次項、一次項、常數項的值，定義F(x)=max(Si(x)),求出F(x)在[0,1000]的最小值。(保證a>0)
解題：
嘗試模擬就會發現所畫出的影象都是下凸的。
——>然而證明的想法並不是很成熟。。
恩，知道上面的以後我們就明白是求單峰函式的最小值了。
於是利用上面的三分法求解。
程式碼（其實我是抄的劉汝佳的♪(^∇^*)）：

#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn=10000+10;
int n,a[maxn],b[maxn],c[maxn];

double F(double x){
    double ans=a[0]*x*x+b[0]*x+c[0];
    for(int i=1;i<n;i++)
        ans=max(ans,a[i]*x*x+b[i]*x+c[i]);
    return ans;
}
int main(){
    int T;
    scanf
 
("%d",&T);
    while(T--){
        scanf("%d",&n);
        for(int i=0;i<n;i++)scanf("%d%d%d",&a[i],&b[i],&c[i]);
        double L=0.0,R=1000.0;
        for(int i=0;i<100;i++){
            double m1=L+(R-L)/3;
            double m2=R-(R-L)/3;
            if(F(m1)<F(m2))R=m2;else L=m1;
        }
        printf
 
("%.4\n",F(L));
    }
    return 0;
}

其實有人已將發現題目中就是求最大值最小，所以經典的思路二分應該也是可以求解的。（然而我並不會，會的大神快來教導我(～ o ～)~）

參考文獻：《演算法競賽入門經典訓練指南》