機器學習基石 作業0

• 1 Probability and Statistics
• 2 Linear Algebra
• 3 Caculus

1 Probability and Statistics

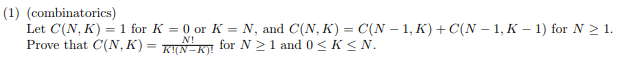
用數學歸納法。N=1時滿足，假定N=n滿足，當N=n+1同樣滿足。得證。

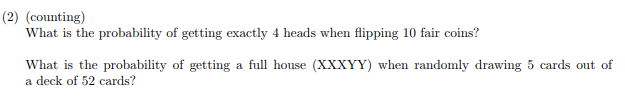
10個挑4個正面 $C_{10}^{}$

假設已知第一次正面，那麼三次都是正面的概率是1/4。而提供的是有一個已知正面，那麼三次裡每一次都有可能。即 $3*1/3*1/4 = 1/4$。

$p(x=-1| |x|=1) = \dfrac{p(x=-1)}{p(|x|=1)} = \dfrac{1/2*1/4}{1/2*1/4+1/2*1/8} = 2/3$

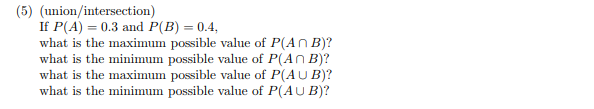
0.3 0 0.7 0.4

2 Linear Algebra

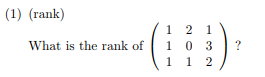
秩為2

$\begin{pmatrix} 1/8 & -5/8 & 3/4 \\ -1/4 & 1/4 & -1/2 \\ 3/8 & -3/8 & 1/4 \end{pmatrix}$

$\lambda_{1} = 4 \ \ \ \ \ \ \ \lambda_{2}=\lambda_{3}=2$
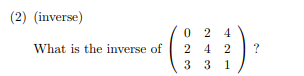
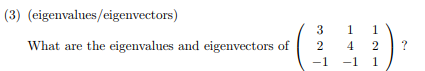
對應特徵向量 $v_{1}= [1\ 2 \ -1] \ \ v_{2}=v_{3} = [1 \ 1 \ -2]$ $v_{2}$和 $v_{3}$只要滿足元素和為0即可，也不用相等

(a) svd分解中 $U$和 $V$都是正交矩陣，直接乘即可。
(b)兩個矩陣相乘得單位陣

(a) $x^{T}ZZ^{T}x$ = $(Z^{T}x)*{Z^{T}x}$ 結果的每個元素都非負，得證
(b)對稱矩陣可以用標準正交陣進行分解，在特徵值都為正時結果的每個元素為正。

$\dfrac{x^{T}x}{|x|}$ $\dfrac{x}{|x|}$
$\dfrac{-x^{T}x}{|x|}$ $\dfrac{-x}{|x|}$
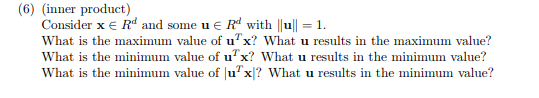
0 當u與x垂直時

3 Caculus

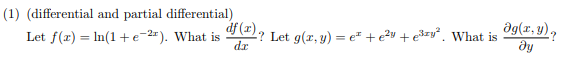
普通求導

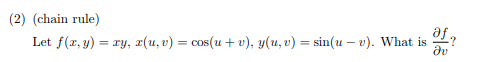
鏈式法則普通求導

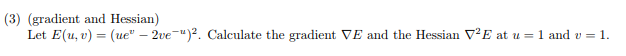
普通求梯度和黑塞矩陣

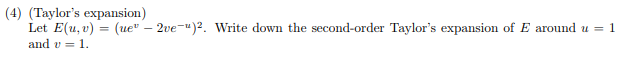
二元泰勒展開 https://zhuanlan.zhihu.com/p/33316479
可以用上(3)中的梯度和黑塞矩陣的結果

求導為0的地方是最小值。因為只有一個矩陣為0的位置，而正無窮與負無窮兩頭對應的結果都是無窮大且值一直大於0。

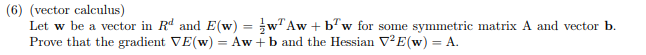
應該是按矩陣乘法裡的每個分量進行求導然後寫會矩陣形式。略難寫。