機器學習基石 作業二

1. 計算一下本來預測對與預測錯時加上噪音導致的錯誤率然後相加即可。
2. 選擇一個 $\lambda$的值讓 $\mu$
   的係數為0。
3. 根據VC bound 公式帶入計算即可，N=46000的時候error最接近0.05。下面的程式碼可以計算不同的N與目標error之間的差距。

def compute(N,err):
    delta = 0.05
    dvc = 10
    res = np.sqrt(8/N*np.log(4*pow(2*N,dvc)/delta))
    return res-err

4. 程式設計計算這幾個不等式的上限。感覺不是很有意思。將N=10000和N=5的時候分別帶入看哪個最小即可。有兩個隱函式需要使用sympy.solve來當做等式解方程。程式碼如下：

dvc = 50
delta = 0.05
N = 5

def origiVC():
    return np.sqrt(8/N*np.log(4*pow(2*N,dvc)/delta))

def rpVC():
    r1 = np.sqrt(2*np.log(2.0*N*pow(N,dvc))/N)
    r2 = np.sqrt(2/N*np.log(1/delta))
    return  r1+r2+1/N

def pvVC():
    epsilon = sympy.symbols('epsilon')
    r1 = sympy.solve(epsilon-sympy.sqrt(1/N*sympy.log(6*((2*N)**dvc)/delta)),epsilon)
    return r1

def dVC():
    epsilon = sympy.symbols('epsilon')
    r1 = sympy.solve(epsilon-sympy.sqrt(0.5/N*(4*epsilon*(1+epsilon) + np.log(4)+dvc*sympy.log(N**2.0)-np.log(delta))),epsilon)
    return r1

def vVC():
    return np.sqrt(16/N*(np.log(2)+dvc*np.log(N*1.0)-np.log(np.sqrt(delta))))

if __name__ == '__main__':
    print(origiVC())
    print(rpVC())
    print(pvVC())
    print(dVC())
    print(vVC())
 

5. 
6. 做錯了。看到個別人的一個解釋。

https://blog.csdn.net/zyghs/article/details/78762070 這個老哥的部落格裡有這題稍微詳細的解釋。還是找規律寫出通式，高中數學真重要.jpg

7. 根據公式，VC維是3
8. 還是將N=1開始慢慢找，發現N=3時能shatter的也是7種。因此得到答案。這相當於是一個二維的positive interval的題目。可以看ppt上關於Positive interval的假設，N個點，可以選擇N+1個位置作為interval的起點或終點。每次的interval需要一個終點一個起點，也就是 $C_{}^{}$
   N + 1 2 C_{N+1}^{2} ，或者起點終點都在最邊上，這兩種是一種情況，都分為全負因此再加一。
   
9. 跟視訊裡講的一樣，d維感知機。答案是d+1。
   
10. 這個題目主要是理解題目意思比較費勁。s是一個d維向量的集合，而且每個d維向量對應一個+1或一個-1。因此無論N多大，能夠將樣例最多分類為 $2^{2^{d}}$種結果，也就是VC維是 $2^{d}$。
11. 三角波調節上下平移取絕對值之後的正負號。好像對於所有N都能夠將其完全shatter。因此事無窮大。
12. 選項1：可以無限遞迴至N=1，顯然不對。 選項2：是個常數不對。選項3：應該是個[ $m_{H}(N),2^{N}$]之間的數，所以可以。選項4：指數是 $d_{vc}/2$，不能保證是上界。
13. 其它選項都沒有疑問。第二個選項確實不太懂。不過第五題引用的部落格裡那個老哥說可能是因為這個函式是跳躍式地增長的。而一個growth函式應該是連續增長的（只要VC維不是0），應該是排列組合的一個性質。我覺得老哥說得對。
14. 交集的部分可能是空，最好的情況也就是等於VC維最小的一個假設集合。不是很好解釋，自行體會。
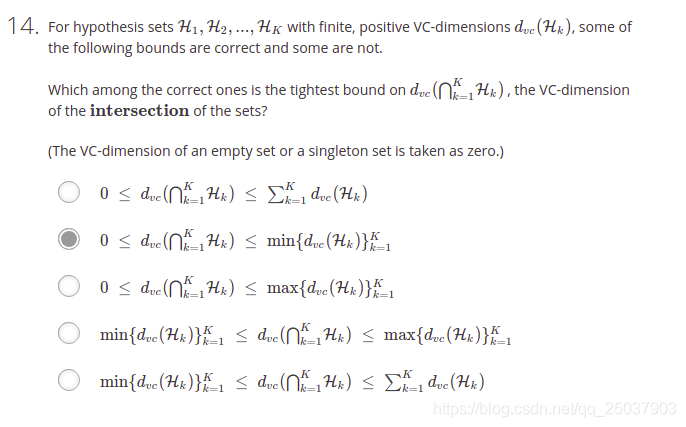
15. 這個並集的下界很好理解，最小也是所有假設集合裡VC維最大的那個的值。而稍微難以解釋。如果每一個假設集合都沒有交集，因此顯然他們的並集的vc維上界需要將所有的vc維都加起來，但是這樣還不夠。因為並集了以後不同的假設集合之間的組合也會帶來一些新的“自由度”。所以應該還有一項。至於為啥是K-1不是非常明確。
16. 將s是正號以及負號， $\theta$大於0還是小於0的情況進行組合一下，簡單計算得出結果。後面幾題需要理解演算法流程進而實現。
    17-18 結果分別是0.15 0.25。需要理解演算法的具體實現。這個演算法主要是選擇正負號s和分隔點 $\theta$。而分隔點可以直接根據每一個數據點 $x$的位置進行選擇。比如題目裡有20個數據，那麼將這20個數據排序好，之後將每一個點的座標作為 $\theta$來比較 $E_{in}$選出最優結果。程式碼如下：

import numpy as np 
import random


def genData(N,noise):
    x = []
    y = []
    for i in range(N):
        x1 = random.uniform(-1,1)
        prob = random.uniform(0,1)
        if prob < noise:
            y1 = -sign(x1,True)
        else:
            y1 = sign(x1,True)
        x.append(x1)
        y.append(y1)
    return np.array(x),np.array(y)

def errorRate(x,y,s,theta,h):
    errorNum = 0
    for i in range(len(x)):
        if y[i] != h(x[i],s,theta):
            errorNum += 1
    return errorNum/len(x)

def hFunc(x,s,theta):
    if s:
        return sign(x-theta,s)
    else:
        return -sign(x-theta,s)

def sign(v,s):
    if v == 0:
        return s
    elif v < 0:
        return -1
    else:
        return 1

def trainDecisionStump(N,noise):
    x,y = genData(N,noise) #N=20,noise=0.2
    E_in = 1
    best_s = True
    best_theta = 0
    thetas = np.sort(x) #排序x用來作為備選的theta
    ss = [True,False] #先遍歷s是正的時候
    for theta in thetas:
        for s in ss:
            E = errorRate(x,y,s,theta,hFunc)
            if E < E_in:
                E_in = E
                best_s = s
                best_theta = theta
    index, = np.where(thetas == best_theta)
    if index[0] == 0:
        best_theta = (-1+best_theta)/2
    else:
        best_theta = (thetas[index[0]-1]+best_theta)/2
    E_out = computeEout(best_s,best_theta)
    return E_in,E_out

def computeEout(s,theta):
    if s:
        return 0.5+0.3*(np.abs(theta)-1)
    else:
        return 0.5-0.3*(np.abs(theta)-1)

def main():
    iteration = 5000
    N = 20
    noise = 0.2
    err_in_sum = 0
    err_out_sum = 0
    for i in range(iteration):
        err_in, err_out = trainDecisionStump(N,noise)
        err_in_sum += err_in
        err_out_sum += err_out 
        if i%100 == 99:
            print("iteration: ",i+1)
    print("total errorRate in sample is",err_in_sum/iteration)
    print("total errorRate out of sample is",err_out_sum/iteration)

if __name__ == '__main__':
    main()

19-20 多維形式的演算法。需要理解多維演算法的流程。每一維度上都選擇一個最好的函式。而最終在這些不同維度最好的函式裡面選擇一個最好的，並且以這個作為最終的多維函式。也就是說最終只選擇某個維度作為分類維度，其它維度都捨棄掉了。最終結果是0.25,0.35。程式碼如下：

import numpy as np 
import random
import requests


def getData(url):
    content = requests.get(url).content
    content = content.decode('utf-8')
    x = []
    y = []
    content = content.split('\n')
    for line in content[:-1]:
        data = line.split(' ')
        y.append(int(data[-1]))
        x1 = data[1:-1]
        for i in range(len(x1)):
            x1[i] = float(x1[i])
        x.append(x1)
    x = np.array(x)
    y = np.array(y)
    return x,y


def errorRate(x,y,s,theta,h,dimension):
    errorNum = 0
    for i in range(len(x)):
        if y[i] != h(x[i][dimension],s,theta):
            errorNum += 1
    return errorNum/len(x)

def hFunc(x,s,theta):
    if s:
        return sign(x-theta,s)
    else:
        return -sign(x-theta,s)

def sign(v,s):
    if v == 0:
        return s
    elif v < 0:
        return -1
    else:
        return 1

def trainDecisionStump(x,y):
    dimensions = len(x[0])
    E_in = 1
    best_s = True
    best_theta = 0
    best_dim = 0
    for dim in range(dimensions):
        thetas = np.sort(x[:,dim]) #排序x用來作為備選的theta
        ss = [True,False] #先遍歷s是正的時候
        for theta in thetas:
            for s in ss:
                E = errorRate(x,y,s,theta,hFunc,dim)
                if E < E_in:
                    E_in = E
                    best_s = s
                    best_theta = theta
                    best_dim = dim
    return best_s,best_theta,best_dim,E_in

def main():
    trainUrl = 'https://www.csie.ntu.edu.tw/~htlin/mooc/datasets/mlfound_math/hw2_train.dat'
    testUrl = 'https://www.csie.ntu.edu.tw/~htlin/mooc/datasets/mlfound_math/hw2_test.dat'
    trainX,trainY = getData(trainUrl)
    testX,testY = getData(testUrl)
    s,theta,dim,err_in = trainDecisionStump(trainX,trainY)
    err_out = errorRate(testX,testY,s,theta,hFunc,dim)
    print("total errorRate in sample is",err_in)
    print("total errorRate out of sample is",err_out)

if __name__ == '__main__':
    main()