機器學習基石 作業三
阿新 • • 發佈:2018-12-06
機器學習基石 作業三
- 代入計算

- 線性迴歸得到的對映函式
的性質問題。顯然對映多次與對映一次效果一樣。其它的可以根據
的性質,秩為d+1,顯然不可逆。特徵值的部分不是非常清楚,大概是根據 的跡等於 得到的。

3. PLA的error的上限。計算一下就知道結果。

4. 可微,顯然。

5. 使用SGD法能夠得到PLA的error。SGD法更新公式
。可以算出其中一個能夠得出
的更新結果。做的時候思路不是很清晰,error與error的梯度有點混。

7. 6-10除了第9題之外都是程式設計題,程式碼如下:
import numpy as np
def E(u,v):
return np.exp(u)+np.exp(2*v)+np.exp(u*v)+u*u-2*u*v+2*v*v-3*u-2*v
def gradU(func,u,v):
return (func(u+0.0001,v)-func(u-0.0001,v))/0.0002
def gradV(func,u,v):
return (func(u,v+0.0001)-func(u,v-0.0001))/0.0002
def update(N):
u,v = 0,0
for i in range(N):
gu = gradU(E,u,v)
gv = gradV(E,u,v)
u = u-0.01*gu
v = v-0.01*gv
return u,v
def newtonUpdate(N):
u,v = 0,0
for i in range(N):
gu = gradU(E,u,v)
gv = gradV(E,u,v)
guu = gradU(lambda u,v:gradU(E,u,v),u,v)
guv = gradU(lambda u,v:gradV(E,u,v),u,v)
gvu = gradV(lambda u,v:gradU(E,u,v),u,v)
gvv = gradV(lambda u,v:gradV(E,u,v),u,v)
hession = np.mat([[guu,guv],[guv,gvv]])
grad = np.array([[gu],[gv]])
delta = hession.I * grad
delta = delta.tolist()
u = u-delta[0][0]
v = v-delta[1][0]
return u,v
def main6():
gu = gradU(E,0,0)
gv = gradV(E,0,0)
print(gu,gv)
def main7():
u,v = update(5)
print(E(u,v))
def main8():
u = 0
v = 0
b = E(u,v)
gu = gradU(E,u,v)
gv = gradV(E,u,v)
guu = gradU(lambda u,v:gradU(E,u,v),u,v)
guv = gradU(lambda u,v:gradV(E,u,v),u,v)
gvu = gradV(lambda u,v:gradU(E,u,v),u,v)
gvv = gradV(lambda u,v:gradV(E,u,v),u,v)
print(guu/2,gvv/2,guv,gu,gv,b)
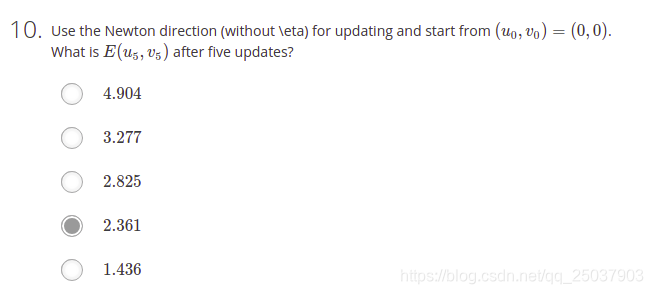
def main10():
u,v = 0,0
u,v = newtonUpdate(5)
print(E(u,v))
if __name__ == '__main__':
main6()
main7()
main8()
main10()


- 這題需要注意,對應的係數不是直接等於求導的結果,二次項有一個0.5的係數,而uv有兩項,加起來是1。emm這題卡了好久,懷疑人生。

9. 牛頓法的下降方向,不太懂,不過貌似是個基礎問題,找了個連結。梯度下降法、牛頓法和擬牛頓法 
10. 
11. 有兩個變數,它的2階非線性對映之後的VC維是
,因此對於6個點的情況是可以shatter的。不過稍微有點疑問,VC維是指最多可能shatter的點的數量,雖然是7但是不知道如何證明能夠shatter這6個給定的點。線性的好說可以眼看,二次的不太明白怎麼證明。

12. 這題比較有意思。把訓練集對映到一個N維的0/1向量。也就是one-hot的形式。因此對於訓練集之外的點對映後的x都是全0的向量,於是結果都是1,又因為實際的分佈中有30%的結果是1,因此
是沒問題的。其他的選項,N個數據就映射了N維,很顯然線性可分(每一維的係數等於對應結果+1或-1即可),因此其它選項都明白了。

13. 程式設計求解。直接使用numpy裡的偽逆方法。程式碼如下:
import numpy as np
import random
def sign(v):
if v > 0:
return +1
else:
return -1
def targetFunc(x1,x2):
r = x1*x1+x2*x2-0.6
return sign(r)
def genData(N):
xs = []
ys = []
for i in range(N):
x1 = random.uniform(-1,1)
x2 = random.uniform(-1,1)
y = targetFunc(x1,x2)
prob = random.uniform(0,1)
if prob < 0.1:
y = -y
xs.append([1,x1,x2])
ys.append([y])
return np.mat(xs), np.array(ys)
def trainLR(x,y):
pseu_inv = np.linalg.pinv(x)
w = pseu_inv*y
return np.array(w)
def errorRate(w,x,y):
yHat = np.array(x*w)
yHat = list(map(sign,yHat))
y = list(map(lambda x: x[0],y))
errorNum = np.sum(np.array(yHat) != np.array(y))
return errorNum/len(y)
def main():
N = 1000
errorSum = 0
for i in range(N):
x,y = genData(1000)
w = trainLR(x,y)
errorSum += errorRate(w,x,y)
print("error in sample is",errorSum/N)
if __name__ == '__main__':
main()
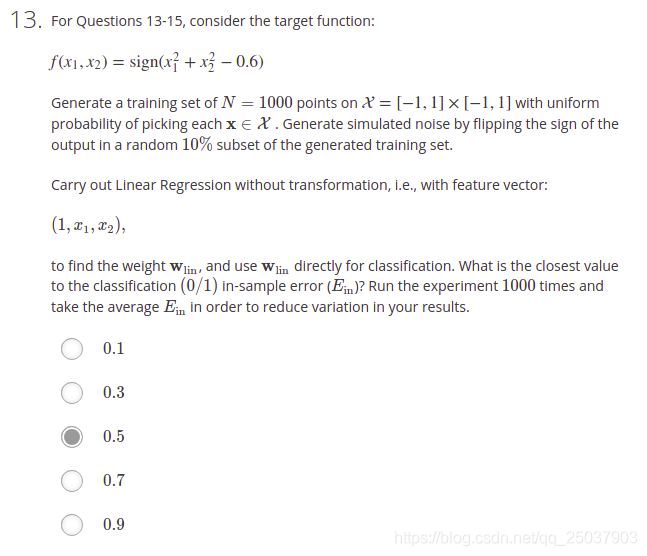
- 先算出使用線性迴歸的結果,然後將題目中的係數代入資料集進行驗證錯誤率最接近的即可。程式碼如下(程式碼是平均了線性迴歸結果的係數肉眼看最接近的,不嚴謹):
import numpy as np
import random
def sign(v):
if v > 0:
return +1
else:
return -1
def targetFunc(x1,x2):
r = x1*x1+x2*x2-0.6
return sign(r)
def genData(N):
xs = []
ys = []
for i in range(N):
x1 = random.uniform(-1,1)
x2 = random.uniform(-1,1)
y = targetFunc(x1,x2)
prob = random.uniform(0,1)
if prob < 0.1:
y = -y
xs.append([1,x1,x2,x1*x2,x1*x1,x2*x2])
ys.append([y])
return np.mat(xs), np.array(ys)
def trainLR(x,y):
pseu_inv = np.linalg.pinv(x)
w = pseu_inv*y
return np.array(w)
def errorRate(w,x,y):
yHat = np.array(x*w)
yHat = list(map(sign,yHat))
y = list(map(lambda x: x[0],y))
errorNum = np.sum(np.array(yHat) != np.array(y))
return errorNum/len(y)
def main():
N = 1000
# errorSum = 0
# wsum = None
# for i in range(N):
# x,y = genData(1000)
# w = trainLR(x,y)
# if wsum is None:
# wsum = w
# else:
# wsum += w
# errorSum += errorRate(w,x,y)
# if i%100 == 0:
# print("iteration:",i+1)
# print("error in sample is",errorSum/N)
# print(wsum/N)
errorSum = 0
w = np.array([[-1],[-0.05],[0.08],[0.13],[1.5],[1.5]])
print(w.shape)
for i in range(N):
x,y = genData(1000)
errorSum += errorRate(w,x,y)
if i%100 == 0:
print("iteration:",i+1)
print("error out of sample is",errorSum/N)
if __name__ == '__main__':
main()

- 程式碼也在上面,代入檢驗即可。

- 跟ppt一樣,寫下來假設函式產生資料集的聯合概率,然後取ln加負號。

17. 上題結果求導即可。

18. 實現邏輯迴歸演算法然後使用測試集進行檢測即可。主要是numpy的使用,程式碼如下(程式碼已經是SGD的演算法,對應更新的地方改一下就行):
import numpy as np
import requests
import random
def getData(url):
content = requests.get(url).content
content = content.decode('utf-8')
x = []
y = []
content = content.split('\n')
for line in content[:-1]:
data = line.split(' ')
y.append(int(data[-1]))
x1 = data[1:-1]
for i in range(len(x1)):
x1[i] = float(x1[i])
x.append([1]+x1)
x = np.mat(x)
y = np.array(y)
return x,y
def sigmoid(s):
return 1/(1+np.exp(-s))
def hypo(w,x):
return sigmoid(x*w)
def gradientOne(w,x,y,i):
res = hypo(w,-y[i]*x[i]).item()*(-y[i]*x[i].T)
return np.array(res.tolist())
def gradient(w,x,y):
N = len(y)
gSum = None
for i in range(N):
if gSum is None:
gSum = gradientOne(w,x,y,i)
else:
gSum += gradientOne(w,x,y,i)
return gSum/N
def logisticRegression(w,x,y):
T = 2000
eta = 0.001
for i in range(T):
#for index in range(len(x)):
g = gradientOne(w,x,y,i%len(y))
w = w - eta*g
if i%100 == 0:
print("iteration",i)
return w
def sign(v):
if v >= 0.5:
return 1
else:
return -1
def errorRate(w,x,y):
yHat = hypo(w,x).tolist()
yHat = list(map(lambda x:sign(x[0]),yHat))
errorNum = np.sum(np.array(yHat) != np.array(y))
return errorNum/len(y)
def main():
trainUrl = 'https://www.csie.ntu.edu.tw/~htlin/mooc/datasets/mlfound_algo/hw3_train.dat'
testUrl = 'https://www.csie.ntu.edu.tw/~htlin/mooc/datasets/mlfound_algo/hw3_test.dat'
trainX,trainY = getData(trainUrl)
testX,testY = getData(testUrl)
w0 = np.array([0]*trainX[0].size)
w0 = w0.reshape(-1,1)
w = logisticRegression(w0,trainX,trainY)
print(w)
errR = errorRate(w,testX,testY)
print("out of sample error rate is",errR)
if __name__ == '__main__':
main()

- 執行即可。

20.

