前言

回溯法 1-求n個元素的集合的冪集中狀態變化樹是一棵滿二叉樹：樹中每個葉子結點的狀態都是求解過程中可能出現的狀態（即問題的解）。
【然而】很多問題用回溯和試探求解時，描述求解過程的狀態樹不是一棵滿的多叉樹

【非滿多叉樹】不是滿的多叉樹：當試探過程中出現的狀態和問題所求解產生矛盾時，不再繼續試探下去，這時出現的葉子結點不是問題的解的終結狀態
此類問題的求解過程可看成是在約束條件下進行先序（根）遍歷，並在遍歷過程中剪去那些不滿足條件的分支

問題

求4皇后問題的所有合法佈局（作為例子，把八皇后問題簡化為4皇后問題）

思路

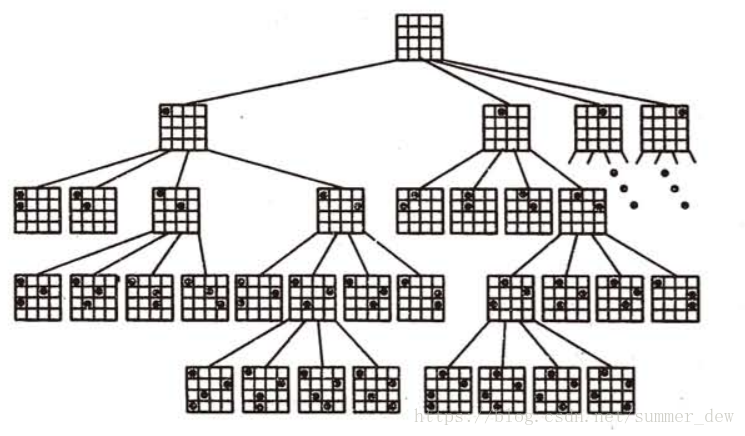
四皇后問題的棋盤狀態樹：

這是一棵四叉樹，樹上每個結點表示一個區域性佈局或一個完整的佈局

【根結點】棋盤的初始狀態，棋盤上無任何棋子
【規則】每個棋子都有4個可選擇的位置
但在任何時刻，棋盤的合法佈局都必須滿足3個約束條件，即任何兩個棋子都不佔據棋盤的同一行、或者同一列、或者同一對角線

求所有合法佈局的過程即為在上述約束條件先根遍歷圖中的狀態樹的過程

做法

遍歷中訪問結點的操作為：判別棋盤上是否已得到一個完整的佈局（即棋盤上是否已擺上4個棋子）

1. 是：輸出該佈局
2. 否：依次先根遍歷滿足約束條件的各棵子樹，即首先判斷該子樹根的佈局是否合法
   1. 合法：先根遍歷該子樹
   2. 否則：剪去該子樹分支

void Trial(int i, int n) {
	// 進入本函式時，在n×n棋盤前i-1行已放置了互不攻擊的i-1個棋子
	// 現從第i行起繼續為後續棋子選擇合適位置
	// 當i>n時，求得一個合法的佈局，輸出之
	if (i>n) 輸出棋盤的當前佈局； //n為4時，即4皇后問題
	else {
		for (j=1; j<=n; j++) {
			在第i行第j列放置一個棋子；
			if (當前佈局合法)
				Trial(i+1, n);
			移走第i行第j列的棋子；
		}
	}
}
 

該演算法可作為回溯法求解的一般模式，類似問題有騎士遊歷、迷宮問題、選最優解問題等