編輯距離演算法詳解:Levenshtein Distance演算法——動態規劃問題
目錄
背景:

我們在使用詞典app時,有沒有發現即使輸錯幾個字母,app依然能給我們推薦出想要的單詞,非常智慧。它是怎麼找出我們想要的單詞的呢?這裡就需要BK樹來解決這個問題了。在使用BK樹之前我們要先明白一個概念,叫編輯距離,也叫Levenshtein距離。詞典app是怎麼判斷哪些單詞和我們輸入的單詞很相似的呢?我們需要知道兩個單詞有多像,換句話說就是兩個單詞相似度是多少。1965年,俄國科學家Vladimir Levenshtein給字串相似度做出了一個明確的定義叫做Levenshtein距離,我們通常叫它“編輯距離”。字串A到B的編輯距離是指,只用插入、刪除和替換三種操作,最少需要多少步可以把A變成B。例如,從aware到award需要一步(一次替換),從has到have則需要兩步(替換s為v和再加上e)。Levenshtein給出了編輯距離的一般求法,就是大家都非常熟悉的經典動態規劃
- d(x,y) = 0 當且僅當 x=y (Levenshtein距離為0 <==> 字串相等)
- d(x,y) = d(y,x) (從x變到y的最少步數就是從y變到x的最少步數)
- d(x,y) + d(y,z) >= d(x,z) (從x變到z所需的步數不會超過x先變成y再變成z的步數) 最後這一個性質叫做三角形不等式。就好像一個三角形一樣,兩邊之和必然大於第三邊。
在自然語言處理中,這個概念非常重要,比如在詞典app中:如果使用者馬虎輸錯了單詞,則可以列出字典裡與它的Levenshtein距離小於某個數n的單詞,讓使用者選擇正確的那一個。n通常取到2或者3,或者更好地,取該單詞長度的1/4等等。這裡主要講編輯距離如何求?至於怎麼實現列出詞典中相似的單詞,詳見寫檢查程式設計題詳解-BK樹演算法。
求編輯距離演算法:
這裡需要有動態規劃的思想,如果之前沒有聽過動態規劃演算法,請參考最少錢幣數(湊硬幣)詳解-2-動態規劃演算法(初窺)。動態規劃演算法通常基於一個遞推公式及一個或多個初始狀態。 當前子問題的解將由上一次子問題的解推出。所以我們首要目標是找到某個狀態和一個地推公式。假設我們可以使用d[ x,y ]個步驟(可以使用一個二維陣列儲存這個值),表示將串x[1...i]轉換為 串y [ 1…j ]所需最少步驟數。
在最簡單的情況下,即在i=0時,也就是說串x為空,那麼對應的d[0,j] 就是x增加j個字元,即需要j步,使得x轉化為y;在j等於0時,也就是說串y為空,那麼對應的d[i,0] 就是x減少 i個字元,即需要i步,使得x轉化為y。這是需要的最少步驟數了。
然後我們再進一步,如果我們想要將x[1...i]經過最少次數的增、刪、改 操作轉換為y[1...j],可以考慮三種情況:
1)假設我們可以在最少a步內將x[1...i]轉換為y[1...j-1],這時我們只需要將x[1...i]加上y[j]就可以完成將x[1...i]轉化為y[1...j],這樣x轉換為y就需要a+1步。
2)假設我們可以在最少b步內將x[1...i-1]轉換位y[1...j],這時我們只需要將x[i]刪除就可以完成將x[1...i]轉換為y[1...j],這樣x轉換為y就需要b+1步。
3)假設我們可以在最少k步內將x[1...i-1]轉換為y[1...j-1],這時我們就需要判斷x[i]和y[j]是否相等,如果相等,那麼我們只需要k步就可以完成將x[1...i]轉換為y[1...j];如果x[i]和y[j]不相等,那麼我們需要將x[i]替換為y[j],這樣需要k+1步就可以將x[1...i]轉換為y[1...j]。
這三種情況是在前一個狀態可以以最少次數的增加,刪除或者替換操作,使得現在串x和串y只需要再做一次操作或者不做就可以完成x[1..i]到y[1..j]的轉換。最後,我們為了保證目前這個狀態(x[1..i]轉換為y[1..j])下所需的步驟最少,我們需要從上面三種情況中選擇步驟最少的一種作為將x[1...i]轉換為y[1...j]所需的最少步驟數。即min(a+1,b+1,k+eq),其中x[i]和y[j]相等,則eq=0,否則eq=1。
具體演算法步驟如下(可以結合者下邊的圖來理解):
1、構造 行數為m+1 列數為 n+1 的陣列,用來儲存完成某個字串轉換所需最少步數,將串x[1..m] 轉換到 串y[1…n] 所需要最少步數為levenST[m][n]的值;
2、初始化levenST第0行為0到n,第0列為0到m。
levenST[0][j]表示第0行第j-1列的值,這個值表示將串x[1…0]轉換為y[1..j]所需最少步數,很顯然將一個空串轉換為一個長度為j的串,只需要j次的add操作,所以levenST[0][j]的值應該是j,其他的值類似。這是最簡單的情形。
3、然後我們考慮一般的情況,如果我們想要將x[1...i]經過最少次數的增、刪、改 操作轉換為y[1...j],就需要將串x和串y的每一個字元兩兩進行比較,如果相等,則eq=0,如果不等,則eq=1。例如,我們可以從x的第一個字母x[0]開始依次和y中的字母(y[0],y[1],y[2],......y[n])進行比較,然後得出相應位置(levenST[1][j])上的最少轉換步驟數。需要考慮三種情況(也就是三個初始的狀態):
- 1)這時levenST[i][j-1]的值a的含義就是最少a步將x[1...i]轉換為y[1...j-1],這時我們只需要將x[1...i]加上y[j]就可以完成將x[1...i]轉化為y[1...j],這樣x轉換為y就需要a+1步。
- 2)levenST[i-1][j]的值b的含義就是在最少b步內將x[1...i-1]轉換為y[1...j],這時我們只需要將x[i]刪除就可以完成將x[1...i]轉換為y[1...j],這樣x轉換為y就需要b+1步。
- 3)而levenS[i-1][j-1]的值k的含義就是在最少k步內將x[1...i-1]轉換為y[1...j-1],這時我們就需要判斷x[i]和y[j]是否相等,如果相等,那麼我們只需要k步就可以完成將x[1...i]轉換為y[1...j];如果x[i]和y[j]不相等,那麼我們需要將x[i]替換為y[j],這樣需要k+1步就可以將x[1...i]轉換為y[1...j]。
最後,我們為了保證目前這個狀態(x[1..i]轉換為y[1..j])下所需的步驟最少,我們需要從上面三種狀態中選擇步驟最少的一種作為將x[1...i]轉換為y[1...j]所需的最少步驟數。即min( levenST[i-1][j] + 1, levenST[i][j-1] + 1, levenST[i-1][j-1] + eq ),其中x[i]和y[j]相等,則eq=0,否則eq=1。
於是我們就可以得出遞推公式:
levenST[i][j] = minOfTreeNum( levenST[i-1][j] + 1, levenST[i][j-1] + 1, levenST[i-1][j-1] + eq );
(遞推公式需要三個初始狀態,即 levenST[i-1][j], levenST[i][j-1]和 levenST[i-1][j-1] ,所以我們需要對陣列 levenST[][] 事先進行初始化,先求出最簡單的狀態下的levenshtein距離)
最後,我們將兩個字串中所有字母都遍歷對比完成之後,將x轉換為y所需最少步驟數就是levenST[m][n]。其中m為字串x的長度,n為字串y的長度。
圖解過程:
1、構造初始化二維陣列levenST[4][5]
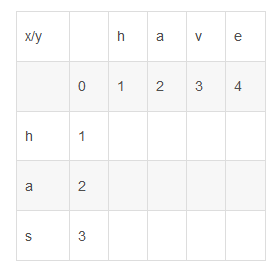
2、從字串has第一個字母開始,依次和y中的字母(y[1...j])進行比較,然後得出相應位置(levenST[1,j])上的最少轉換步驟數。

如果兩個字母相等,則在從此位置的左+1,上+1,左上+0三個數中獲取最小的值存入;若不等,則在從此位置的左,上,左上三個位置中獲取最小的值再加上1。如下圖,首先對比字串x中第一個字母h和字串y中第一個字母h,發現兩個字母相等,所以對比左、上、左上三個位置得出最小值0存入levenST[1][1],接著依次對比‘h''a',‘h'
'v',‘h'
'e'。得出h字串和h,ha,hav,have四個字串的編輯距離。
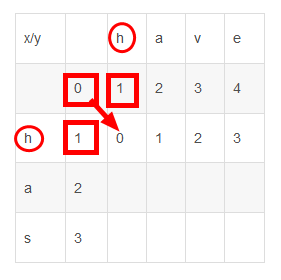
3、接著將字母a依次和have中字母對比,得出ha字串和h,ha,hav,have四個字串的編輯距離。

4、接著將字母s依次和have中字母h,a,v,e對比,得出has字串和h,ha,hav,have四個字串的編輯距離。

最後一個即為單詞has和have的編輯距離,
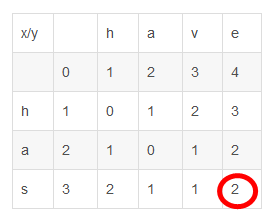
求出編輯距離,就可以得到兩個字串的相似度 Similarity = (Max(x,y) - Levenshtein)/Max(x,y),其中 x,y 為源串和目標串的長度。
| x/y | h | a | v | e | |
| 0 | 1 | 2 | 3 | 4 | |
| h | 1 | 0 | 1 | 2 | 3 |
| a | 2 | 1 | 0 | 1 | 2 |
| s | 3 | 2 | 1 | 1 | 2 |
C++程式碼如下:
#include <iostream>
#include <string>
using namespace std;
int minOfTreeNum(int a, int b, int c) //返回a,b,c三個數中最小值
{
int minNum = a;
if(minNum > b )
{
minNum = b;
}
if(minNum > c )
{
minNum = c;
}
return minNum;
}
int levenSTDistance(string x, string y) //計算字串x和字串y的levenshtein距離
{
int lenx = x.length();
int leny = y.length();
int levenST[lenx+1][leny+1]; //申請一個二維陣列存放編輯距離
int eq = 0; //存放兩個字母是否相等
int i,j;
//初始化二維陣列,也就是將最簡單情形的levenshtein距離寫入
for(i=0; i <= lenx; i++)
{
levenST[i][0] = i;
}
for(j=0; j <= leny; j++)
{
levenST[0][j] = j;
}
//將串x和串y中的字母兩兩進行比較,得出相應字串的編輯距離
for(i=1; i <= lenx; i++ )
{
for(j=1; j <= leny; j++)
{
if(x[i-1] == y[j-1])
{
eq = 0;
}else{
eq = 1;
}
levenST[i][j] = minOfTreeNum(levenST[i-1][j] + 1, levenST[i][j-1] + 1, levenST[i-1][j-1] + eq);
}
}
return levenST[lenx][leny];
}
int main()
{
string a,b;
int levenDistance;
cin >> a;
cin >> b;
levenDistance = levenSTDistance(a,b);
cout << "Levenshtein Distance:" << levenDistance << endl;
return 0;
}
總結:
動態規劃演算法通常基於一個遞推公式及一個或多個初始狀態。 當前子問題的解將由上一次子問題的解推出。關鍵是找到這個遞推公式。需要多加練習。
參考資料: (這是java版程式碼) 編輯距離演算法詳解:Levenshtein Distance演算法
