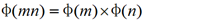概述

  本文旨在說明RSA加密演算法的原理及實現，而其相關的數學部分的證明則不是本文內容。

版權說明

著作權歸作者所有。

商業轉載請聯絡作者獲得授權，非商業轉載請註明出處。

發表日期： 2016年2月29日

來源：CSDN

RSA簡介

  1977年，三位數學家Rivest、Shamir 和 Adleman 設計了一種演算法，可以實現非對稱加密。這種演算法用他們三個人的名字命名，叫做RSA演算法。從那時直到現在，RSA演算法一直是最廣為使用的"非對稱加密演算法"。毫不誇張地說，只要有計算機網路的地方，就有RSA演算法。

                                                                                   -- 摘自網路

數學背景

  此部分旨在補充本文的完整性。如果說你已經瞭解，或是不想了解此部分內容。那麼可以直接跳過此部分的閱讀。

  雖說只是補充說明（只能是補充的原因是因為博主的數學也是比較差的-_-!!!），但是此部分的內容卻是相當重要的。博主還是希望可以重新閱讀一下此部分。

1.互質

  從小學開始，我們就瞭解了什麼是質數。互質是針對多個數字而言的，如果兩個正整數，除了1以外，沒有其他公因子，那麼就稱這兩個數是互質關係（注意，這裡並沒有說這兩個數一定是質數或有一個為質數。比如15跟4就是互質關係）。以下有一些關於質數與互質的性質：

• 質數只能被1和它自身整除
• 任意兩個質數都是互質關係
• 如果兩個數之中，較大的那個數是質數，則兩者構成互質關係
  
• 如果兩個數之中，較小的那個數是質數，且較大數不為較小數的整數倍，則兩者構成互質關係
  
• 1和任意一個自然數是都是互質關係
  
• p是大於1的整數，則p和p-1構成互質關係
  
• p是大於1的奇數，則p和p-2構成互質關係
  

2.尤拉函式

  尤拉函式是求小於x並且和x互質的數的個數。其通式為：φ(x) = x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn)。

  其中p1, p2……pn為x的所有質因數，x是不為0的整數。看到這裡是不是有一些頭疼，太理論的東西的確不夠具象。我們且不去理會後面公式計算與論證，因為已經超出本文的範圍了。就前一句來說說吧，尤拉函式是求小於x並且和x互質的數的個數。這裡我可以列舉一個例子：

  令x = 16，那麼x的所有質因數為：φ(16) = 16 * (1 - 1/2) = 8

  我們也可以枚舉出所有比16小，且與16互質的數：1, 3, 5, 7, 9, 11, 13, 15

  現在也給出部分尤拉函式的性質：

• 若n是素數p的k次冪，，因為除了p的倍數外，其他數都跟n互質
  
• 尤拉函式是積性函式——若m,n互質，
  
• 當n為奇數時，
  
• p是素數，，φ(p)稱為p的尤拉值
  

  尤拉函式更多參考請見這裡的連結。

3.模反元素

定義：如果兩個正整數a和n互質，那麼一定可以找到整數b，使得 ab-1 被n整除，或者說ab被n除的餘數是1。

關於模反元素的求解，使用的是樸素的解法。如果讀者想要更進一步瞭解的話，請自行搜尋其他解法（比如：輾轉相除法、歐幾里德演算法）。

RSA原理

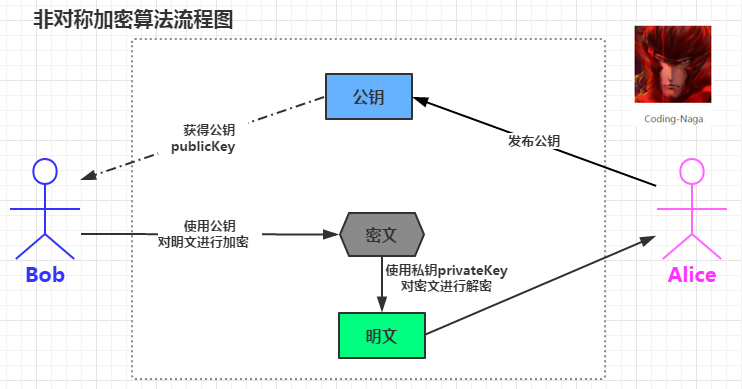
  在RSA原理之前，我想還是有必要了解一下非對稱加密演算法的加密跟解密過程。下面就是一幅非稱加密演算法的流程圖。

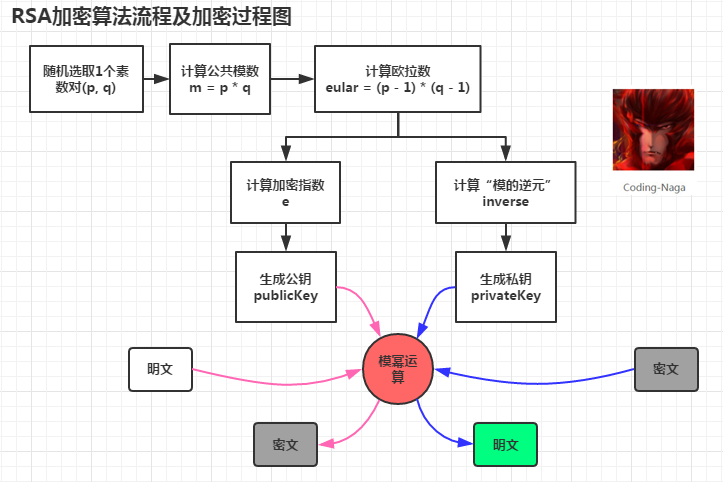
  在此可以看到，非對稱加密是通過兩個金鑰（公鑰-私鑰）來實現對資料的加密和解密的。公鑰用於加密，私鑰用於解密。對於非對稱的加密和解密為什麼可以使用不同的金鑰來進行，這些都是數學上的問題了。不同的非對稱加密演算法也會應用到不同的數學知識。上面也對RSA中使用的數學問題做了一個小小的介紹。現在就來看看RSA演算法是怎麼來對資料進行加密的吧，如下是一幅RSA加密演算法流程及加密過程圖。

RSA應用

1. 例項模型

  就以上圖中的Bob和Alice來舉例吧。

  現在Alice通過金鑰生成器生成了一對金鑰（公鑰-私鑰）。只把公鑰對外公開了。並說，你有什麼要跟我說的，就用模冪運算和公鑰加密後發給我吧。

  此時，Bob已經獲得了Alice釋出的公鑰。使用模冪運算對明文進行了加密，就把加密後的密文傳送給了Alice。

  Alice獲得Bob發來的密文並沒有使用公鑰對密文進行解密，並獲得了明文。因為解密過程需要使用的金鑰是私鑰。

2. RSA演算法實現

  下面的程式碼只是根據RSA演算法的定義，使用Java開發語言實現。且這裡只是展示了一些關鍵步驟，完整過程可以參見下面的原始碼下載文件。

public class RSA {    
    /**
     * 獲得(公/私)金鑰
     */
    public final Map<String, RSAKey> getCipherKeys() {
        ...
        int[] primes = getRandomPrimes(2);
        int modulus = modulus(primes[0], primes[1]);
        int euler = euler(primes[0], primes[1]);
        int e = cipherExponent(euler);
        int inverse = inverse(euler, e);
        publicKey.setExponent(e);
        publicKey.setModulus(modulus);
        privateKey.setExponent(inverse);
        privateKey.setModulus(modulus);
        ...
    }
    
    /**
     * 加密
     */
    public int encode(int plaintext, RSAPublicKey key) {
        return modularPower2(plaintext, key.getExponent(), key.getModulus());
    }
    
    /**
     * 解密
     */
    public int decode(int chipertext, RSAPrivateKey key) {
        return modularPower2(chipertext, key.getExponent(), key.getModulus());
    }

    // 隨機生成count個素數
    private final int[] getRandomPrimes(int count) {
        ...
        try {
            primeLabels = FileReadUtils.readLines("./data/prime_table");
        } catch (IOException e) {
            e.printStackTrace();
        }
        for (int i = 0; i < primes.length; i++) {
            primes[i] = Integer.parseInt(primeLabels.get(indexs.get(i)));
        }

        return primes;
    }

    // 計算公共模數
    private final int modulus(int p, int q) {
        return p * q;
    }

    // 計算尤拉數
    private final int euler(int p, int q) {
        return (p - 1) * (q - 1);
    }

    // 計算加密指數
    private final int cipherExponent(int euler) {
        Random random = new Random();

        int e = 7;
        do {
            e = random.nextInt(euler - 1);
        } while (!isCoprime(e, euler) || e <= 1);

        return e;
    }

    // 判斷兩個數互素
    private final boolean isCoprime(int number1, int number2) {

        int sqrt = (int) Math.sqrt(Math.max(number1, number2));
        for (int i = 2; i <= sqrt; i++) {
            if (number1 % i == 0 && number2 % 2 == 0) {
                return false;
            }
        }

        return true;
    }

    // 計算“模的逆元”
    // (d * e) ≡ 1 mod euler
    private final int inverse(int euler, int e) {
        ...
        while (flag) {
            q = m[2] / n[2];
            for (int i = 0; i < 3; i++) {
                temp[i] = m[i] - q * n[i];
                m[i] = n[i];
                n[i] = temp[i];
            }
            if (n[2] == 1) {
                if (n[1] < 0) {
                    n[1] = n[1] + euler;
                }
                return n[1];
            }
            if (n[2] == 0) {
                flag = false;
            }
        }
        return 0;
    }
    
    // 模冪運算
    private final int modularPower(int base, int e, int modular) {
        int result = 1;
        do {
            if (isOdd(e)) {
                result = (result * (base % modular)) % modular;
                e -= 1;
            } else {
                base = (base * base) % modular;
                e /= 2;
            }
        } while (e > 0);
        
        result %= modular;
        
        return result;
    }
}

RSA演算法判別

RSA演算法優點

1. 不需要進行金鑰傳遞，提高了安全性
2. 可以進行數字簽名認證

RSA演算法缺點

1. 加密解密效率不高，一般只適用於處理小量資料（如：金鑰）
2. 容易遭受小指數攻擊

Ref

原始碼下載