最近在回顧PCA方面的知識，發現對於之前的很多東西有了新的理解，下面和大家分享下我的一些個人的理解

1.我們為什麼要用PCA，它能解決我什麼問題？

　　PCA（Principal Component Analysis），主成成分分析，常用於高維資料的降維。在企業級環境中，最終用於模型訓練的資料集往往維度很高，佔用記憶體空間更大。PCA的出現，能保證儘量保留資料更完整資訊的同時，將資料降低到更低的維度，這樣不僅佔用記憶體空間更小，模型訓練速度也明顯加快！ （這裡的模型訓練的速度的加快是   降維之前訓練所用的時間  對比 降維所用的時間 + 降維之後訓練所用的時間

2.PCA的理論分析

　　PCA的目標:

　　　　　　　　2.1：將原始資料集通過降維的方式，在新的座標系下表示，新的座標系的維度遠低於原始維度。

　　　　　　　　2.2：在新的座標系下的表示應儘量保留相對完整的資訊。

　　對於2.2我們知道，完整的資訊指的是資料間的差異。例如我們在做模型訓練的時候，往往希望訓練資料的分佈是涵蓋了所有的情況一樣。我們用方差來衡量資料間的離散程度，這也是新座標下的衡量指標，我們要找到這樣的一組座標系，使得原始資料在新座標系下的方差最大。

3.準備工作

　　進行降維之前，讓我們來做些準備工作。首先對資料進行0均值歸一化，之後再做標準化處理。使得所有資料在同一量綱。

4.數學推導

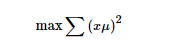
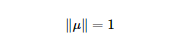
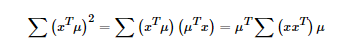
                上式中的μ為空間中的一個向量，x為經過特徵工程處理過後的矩陣。第一個式子為我們的目標函式，第二個為最優解的約束，問題為在約束空間內求最優解的問題，用拉格朗日乘子來求解。

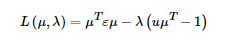　　　　得到下面的結果：

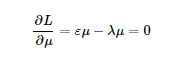
　　　　其中我們使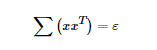，為協方差矩陣。所以我們知道μ就是e的主特徵向量。（關於特徵向量和特徵值的一些概念，可以參靠一些資料來複習下）

　　　　我們的原始問題在此刻即轉變為求e矩陣的TOPk個特徵值對應的k個特徵向量的問題

5.選幾個？

              對應最終的特徵向量，我們選取幾個，最終資料降低到幾維度，那麼，我們要怎麼選取？

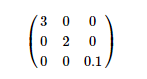
　　　　假設上式為降維後對應的特徵向量，那麼根據特徵值佔比來選擇最終保留的維度，即如果降低到1維  此時的特徵值佔比為(3/3+2+0.1)，如果降低到二維度，此時的特徵值佔比為(3+2/3+2+0.1)

　　　　如果要求資訊量保留95%，那麼根據特徵值佔比與目標值做比較，達到要求即可。

（有一些問題沒有討論，後續完善！之後會上程式碼做比較！）

參考資料：吳恩達機器學習公開課

　　　　　馬同學高等數學公眾號