前言

在用資料對模型進行訓練時，通常會遇到維度過高，也就是資料的特徵太多的問題，有時特徵之間還存在一定的相關性，這時如果還使用原資料訓練模型，模型的精度會大大下降，因此要降低資料的維度，同時新資料的特徵之間還要保持線性無關，這樣的方法稱為主成分分析（Principal component analysis，PCA），新資料的特徵稱為主成分，得到主成分的方法有兩種：直接對協方差矩陣進行特徵值分解和對資料矩陣進行奇異值分解（SVD）。

一、主成分分析基本思想

  資料X由n個特徵降維到k個特徵，這k個特徵保留最大資訊（方差）。對原座標系中的資料進行主成分分析等價於進行座標系的旋轉變化，將資料投影到新的座標系下，新座標系的第一座標軸表示第一主成分，第二座標軸表示第二主成分，以此類推。資料在每一軸上的座標值的平方表示相應變數的方差，PCA的目標就是方差最大的變數，才能保留儘可能多的資訊，因為方差越大，表示資料分散程度越大，所包含的資訊也就越多。

二、PCA的基本步驟

• step1：對資料進行規範化（也稱為標準化），因為涉及距離計算，因此要消除量綱的影響；
  這裡的資料標準化採用z-score：X = X - mean(X) / std(X)
• step2：對資料X進行旋轉變化（前言提到的兩種方法）

三、數學推導

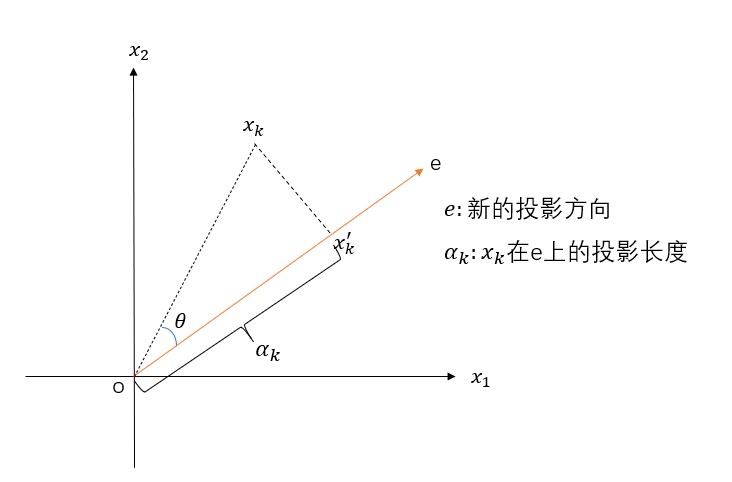
  假設X是m*n的矩陣，\(x_k\)是投影前的資料(k=1,2,…,n)，\(x_k^{'}\)是投影后的資料，e是新的座標軸。投影長度\(α_k=e^tx_k\)，可以將\(e^t\)看成是cosθ，新資料\(x_k^{'}\)在新座標軸e下的座標為\(α_k e\)，表示從原點出發，沿著e方向走了\(α_k\)距離。根據方差最大的原則，即\(α_k\)要最大，由勾股定理\(\alpha_k^2+\left \| x_kx_k{'}\right \|^2=\left\|o x_k\right\|^2\)可知，當\(α_k\)最大時，\(\left\|x_kx_k^{'}\right\|^2\)要最小，因此轉換成求\(\left\|x_kx_k^{'}\right\|^2\)最小，約束條件是\(\left\|e\right\|=1\)，數學表示式為：

\[\begin{cases} min J(e)=\sum_{i=1}^n\left\|x_k^{'}-x_k\right\|^2\\ s.t. \left\|e\right\|=1 \end{cases} \]

1. 完整的數學推導（結合第一部分的圖）

\(min J(e)\\ =\sum_{i=1}^n\left\|x_k^{'}-x_k\right\|^2\\ =\sum_{i=1}^n\left\|\alpha_ke-x_k\right\|^2\\ =\sum_{i=1}^n\alpha_k^2\left\|e\right\|^2 - 2\sum_{i=1}^n\alpha_ke^tx_k + \sum_{i=1}^n\left\|x_k\right\|^2\\ =\sum_{i=1}^n\alpha_k^2-2\sum_{i=1}^n\alpha_k^2+\sum_{i=1}^n\left\|x_k\right\|^2\\ =-\sum_{i=1}^n\alpha_k^2+\sum_{i=1}^n\left\|x_k\right\|^2\\ =-\sum_{i=1}^ne^tx_kx_k^te+\sum_{i=1}^n\left\|x_k\right\|^2\)

要使\(-\sum_{i=1}^ne^tx_kx_k^te+\sum_{i=1}^n\left\|x_k\right\|^2\)最小，由於\(\sum_{i=1}^n\left\|x_k\right\|^2\)不包含e，因為轉換為求\(\sum_{i=1}^ne^tx_kx_k^te\)的最大值，同時記\(S=\sum_{i=1}^nx_kx_k^t\)，實際上，S是協方差X的協方差矩陣，問題可轉化為

\[\begin{cases} max\quad e^tSe\\ s.t. \quad \left\|e\right\|=1 \end{cases} \]

對於上述優化問題，可以用拉格朗日乘子法求解：\(u=e^tSe-\lambda(e^te-1),\frac{\partial u}{\partial e} = 2Se-2\lambda e=0\)，解得：\(Se = \lambda e\)

可以看出，滿足條件的投影方向e(k個)是協方差矩陣S的前k大特徵值對應的特徵向量，因此PCA轉化為求資料X的協方差矩陣的特徵值，將特徵值降序排序，對應的特徵向量構成的矩陣就是所求的旋轉矩陣

2. 求旋轉矩陣

• 基於特徵值求解
• 基於奇異值分解SVD

2.1 基於特徵值求解

  就是一般的矩陣求特徵值和特徵向量的問題，此處不做詳細介紹，需要注意的是，是對資料X的協方差矩陣\(X^TX\)求特徵值和特徵向量，前k個特徵向量構成的矩陣P（此處預設P已經按照特徵值的大小順序進行排列，維度為n*k），那麼新資料\(newX = X*P\),則newX由X的\(m*n\)變成\(m*k(k<n)\)，此時資料已經降低維度了。

2.2 基於SVD求解PCA

三、奇異值分解SVD

3.1 什麼是奇異值分解

  對於任意的矩陣\(A\in\mathbb{R}^{m*n}\)，都可以將A分解成三個矩陣：

\[A=U\sum V^T,U\in\mathbb{R}^{m*m},\sum\in\mathbb{R}^{m*n},V\in\mathbb{R}^{n*n} \]

並且U和V是正交陣，\(\sum\)是對角陣,即

\[UU^T=UU^{-1}=I,VV^T=VV^{-1}=I \]

3.2 奇異值分解的幾何解釋

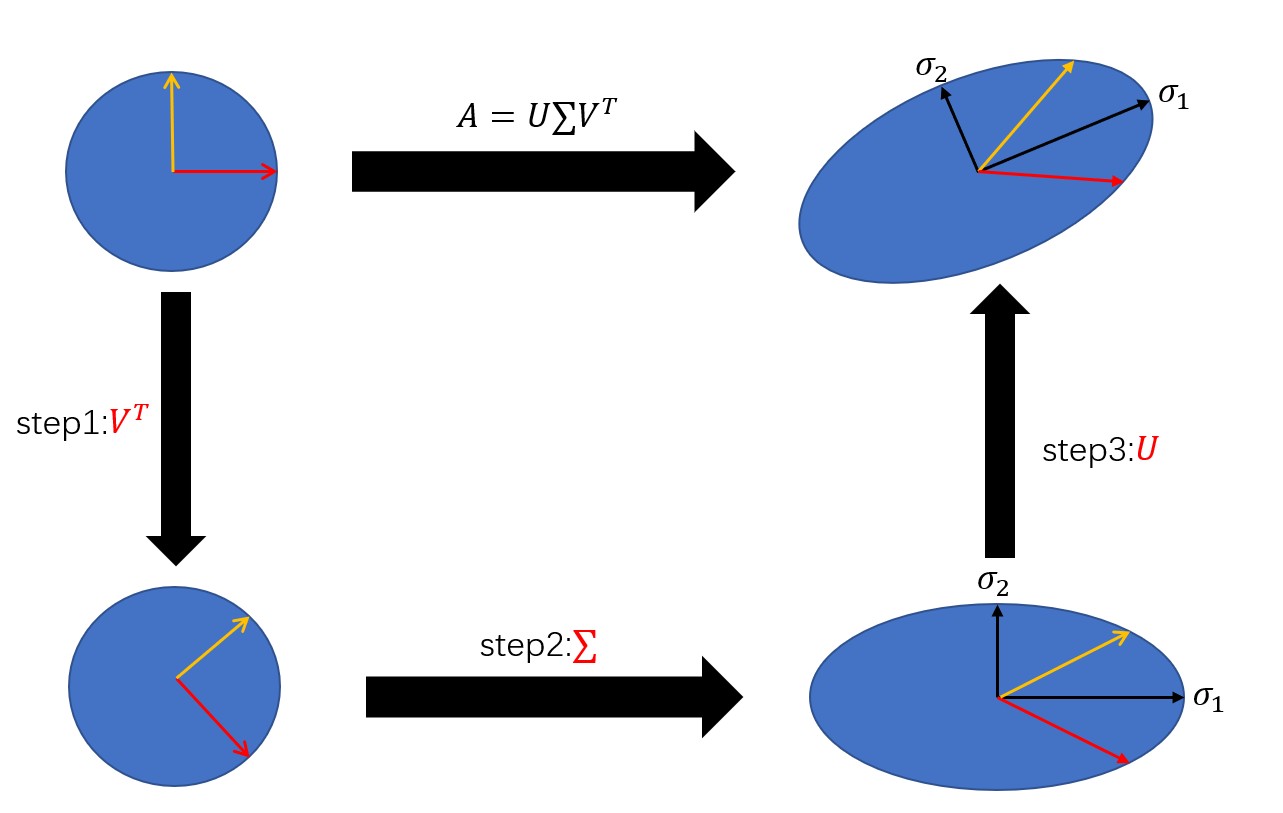
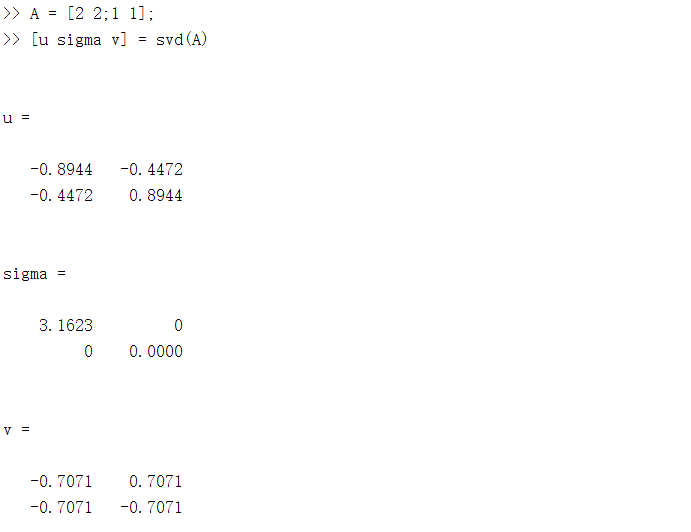
  本質上來說，奇異值分解是一個線性變換，對矩陣A進行奇異值分解可以看成是用一組正交基先進行旋轉\((V^T e)\)，再進行座標縮放\((\sum V^T e)\)，最後再進行座標旋轉\((U\sum V^T e)\)，經過這三步操作，正交基可以變換成A，下面是一個簡單的例子，用MATLAB可以對任意矩陣進行奇異值分解，並且輸出三個矩陣。

3.3 如何求解\(U,\sum,V^T\)

  (以下由於編輯問題，會出現幾個\(\sum^T\)的T出現在\(\sum\)上面)

  對於任意的矩陣都能進行因子分解，這顯然是SVD最大的好處，但關鍵是如何求解三個因子矩陣呢？

3.3.1 求解U

已知\(A=U\sum V^T\),則有

\[AA^T=(U\sum V^T)(U\sum V^T)^T=U\sum V^TV\sum^TU^T=U(\sum\sum^T)U^T \]

又因為U是正交陣，因此有

\[U^T=U^{-1},AA^T=U(\sum\sum^T)U^{-1} \]

左右各乘以\(U^{-1}\)，可以得到

\[AA^TU=U(\sum\sum^T) \]

也就是U是矩陣\(AA^T\)的特徵向量，\((\sum\sum^T)\)是特徵值。

3.3.2 求解V

與求解U類似，通過\(AA^T\)來求解，最終可以得到

\[A^TAV=V(\sum^T\sum) \]

也就是V是矩陣\(A^TA\)的特徵向量，\((\sum^T\sum)\)是特徵值

3.3.3 對角矩陣\(\sum\)

\(\sum\)裡的元素成為奇異值，從3.3.1和3.3.2可以看出，對角矩陣\(\sum\)的奇異值是\(AA^T\)和\(A^TA\)的特徵值的平方根，並且奇異值一定不小於0.以下是簡單的證明：
令\(\lambda\)是\(A^TA\)的一個特徵值，x是對應的特徵向量，則

\[\left\|Ax\right\|^2=x^TA^TAx=\lambda x^Tx=\lambda\left\|x\right\|^2 \]

\[\lambda=\frac{\left\|Ax\right\|^2}{\left\|x\right\|^2}\geq0 \]

而奇異值\(\sigma\)是\(\lambda\)的平方根，因此也大於等於0.

3.3.4 SVD與PCA的關係

PCA的目標是求協方差矩陣\(X^TX\)的特徵向量和特徵值，而協方差矩陣的特徵向量就是矩陣X奇異值分解後的右奇異向量V,用下圖來說明PCA與SVD的關係

因此，經過PCA處理得到的新資料，其實就是對資料X做奇異值分解，然後乘上右奇異矩陣，或者左奇異矩陣乘上對角矩陣！

四、總結

  PCA是一種降維技術，主要用在特徵提取。對於PCA，有兩種方式：直接對資料的協方差矩陣進行特徵向量的求解；對資料進行奇異值分解。實際上，後者會更優於前者。因為求解協方差矩陣的特徵值以及特徵向量時，有時會出現特徵值為虛數，那麼這時候演算法會失效，而SVD求解出來的奇異值一定是非負數。除此之外，其實可以把PCA看做是對SVD的一種包裝，如果實現了SVD，那麼PCA也就實現了，而且更好的是，用SVD可以得到兩個方向的PCA，而直接分解協方差矩陣，只能得到一個方向的PCA