人工智慧和資料分析相關的線性代數知識。比如什麼是向量，什麼是矩陣，矩陣的加減乘除。矩陣對角化，三角化，秩，QR法，最小二法。等等

　　向量：

　　高中數學中都學過複數，負數表示式是：

　　a+bi

　　複數實際上和二維的向量是異性同構的。所謂異性同構，是一個很嚴格的數學定義，這裡不是重點，不做介紹。我們可以近似的把它理解為本質是一樣的，只是外形不同，就如正直的紳士和善良的乞丐那樣。唯一的不同僅僅是外形。回憶下高中我們是如何在一個平面上描述負數的。

　　既然複數和二維向量是一個東西，僅僅是外表不同，那麼向量線上性代數中如何描述呢。

　　座標描述：

　　幾何描述：

　　二維的向量在二維向量空間中和複數在複平面中是一樣的。一個箭頭帶著常常的尾巴，箭頭代表著它的方向，尾巴說明它是有長度的。向量像一支支離弦之箭，在向量空間翱翔。向量空間是一個十分重要的數學概念。它包括很多子空間，你比如歐幾裡向量空間、拓撲向量空間、賦範空間、預希耳伯特空間、酉空間(複數向量空間)。每個空間都有它的特別之處和獨有的操作法則。我們關注的重點是歐幾裡空間，可能以後會稍微提一下賦範空間，其它的這裡不做描述，儘管他們有些十分十分重要，和資料分析也密切相關。比如拓撲向量空間。但是它實在太難了，如果你不打算當數學家的話，還是不要去招惹它。如果你感興趣，我們可以私下聊。

　　我們一直在說二維向量，那麼多維向量又是什麼樣呢。

　　例如座標描述四維向量：

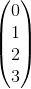
　　幾何描述在有限維度向量空間均和二維空間一樣。

　　和複數中的模類似，在歐幾裡空間中存在範數2，它是由標積派生而出。標積的定義如下：

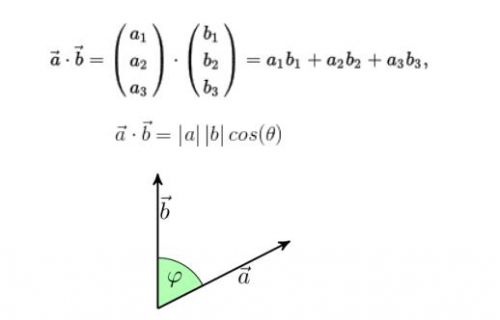
　　當時：

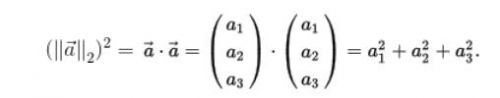
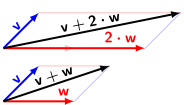
　　向量的加：

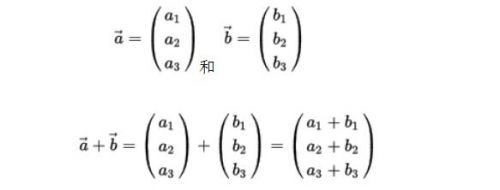
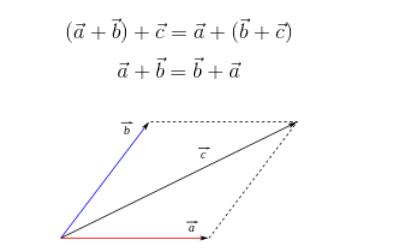
　　向量加法適用結合律和交換律。

　　向量的減：

　　向量的三角不等式：

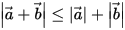
　　此不等式成立的原因，三角形兩邊之和大於第三邊。

　　注：向量可以在歐幾裡空間任意平移，不改變向量本身。

　　向量的除法：

　　目前數學上還沒有這個定義，如果你能定義出向量除法，並且合理。那菲爾茨獎肯定頒發給你。

　　叉積：

　　兩個向量的叉積又是向量，其方向垂直於這兩個向量撐起的平面，其長度為：

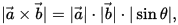
　　這個值恰恰也是上面平面的面積。

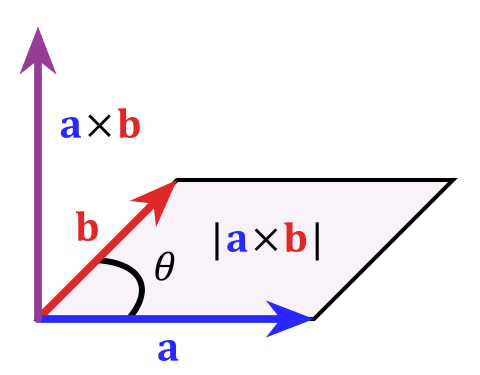
　　在卡迪爾座標下，叉積可表示成：

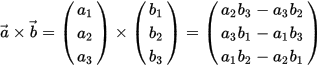
　　叉積滿足負交換律。

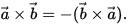
　　交叉乘積：

　　人們通過下面的等式定義交叉乘積：

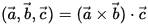
　　它的結果是一個標量。這個標量等於這三個向量撐起平行六面體的體積(作業?)

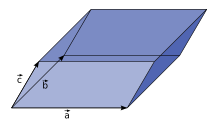
　　如果這三個向量構成右手系統，則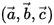是正值，反之，假如構成左手系統。則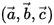是負值。如果這些向量是線性相關。則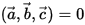

　　向量的歸一化：

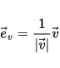
　　(選學)向量的基底變換

　　通常我們遇到向量都是藉助於歐幾裡空間的卡迪爾座標系統標準基底來描述的。什麼是基底呢。

　　基底定義：基底是一個向量空間的子集。這個子集不僅能夠派生出整個向量空間，也就是說任意一個這個向量空間的向量都可以通過這個基底唯一表達。這個我們稱之為派生系統。而且子集中各元素線性不相關。(房子理論)

　　如何派生出整個向量空間?

　　假設V是一個n維向量空間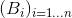，，是一個V的一個基底。那麼我們可以這樣來表達整個V向量空間。

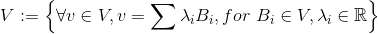
　　線性不相關：

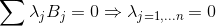
　　現在我們把基底限制到單位卡迪爾座標系統標準基底基底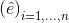，也就是：

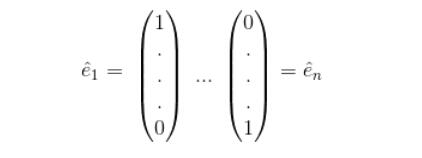
　　例子：假如向量V1=(1,7,9)是關於標準基底的向量，試用基本基底展開這個向量。

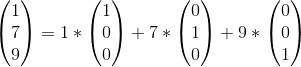
　　我們把上面的例子普通化到n維空間,得到如下公式，

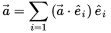
　　如果我們選擇非標準基底，結果會怎樣呢?

　　假如向量V1=(1,7,9)是關於標準基底的向量，現有另一個也是關於標準基底向量空間基底，((1,1,0)，(0,1,0)，(0,0,1)，請嘗試用這個基底來表示V1。

　　辦法：我們嘗試把V1分別分解到這三個向量上;公式如下：

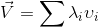
　　這裡向量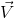是我們的V1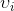，是我們這裡的基底向量中的某一個。由此可得：

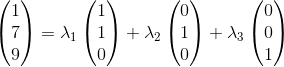
　　求上面等式可得：

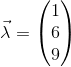
　　這個就是向量V1在新基底下的列矢量表述形式。

　　我們可以看到同一個向量在不同的基底下列的表述完全是不一樣的。這就要求我們，在做向量運算時，一定要注意兩點：

　　1. 這個向量是在哪一個基底下被描述的。

　　2. 各向量之間的運算必須在同一基底下才是正確的。

　　上面所講的內容就是向量的基底變換。它主要應用於一些與向量運算，矩陣運算相關的資料處理，人工智慧問題。通過基底變換很多複雜的矩陣變得十分簡單。節省大量的運算時間。

　　注意：標積中的兩個向量必須關於相同基底，不同基底必須轉化成相同基底才能運算。

　　矩陣

　　(選學)域(體)和環：

　　(代數學)域，有些書也稱作體，是一個帶有‘+’和‘*’操作的特殊集合。並且這個集合裡的任意元素都滿足下列特性。

　　1. 加法特性：

　　A.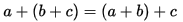結合律

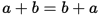　　B.交換律

　　C.中性元素‘0’元素存在且滿足0+a=a(中性元素就是說任何元素與其做+操作結果還是該元素本身)

　　D. 逆元素—a存在，即滿足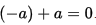(任何元素的逆元素與該元素進行加操作結果都等於中性元素)

　　2. 乘特性

　　A.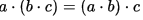結合律

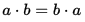　　B.交換律

　　C. 中性元素‘1’元素存在且滿足1*a=a(中性元素就是說任何元素與其做‘*’操作結果還是該元素本身)

　　D. 逆元素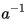存在：對於任意存在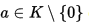且滿足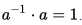：任何元素的逆元素與該元素進行加操作結果都等於中性元素)

　　3. 分配率(‘+’和‘*’操作結合)

　　左分配律：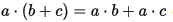

　　右分配律：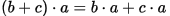

　　實數，有理數，和複數都是典型的域。

　　環，環是另一個代數概念，他的定義與體區別不多，唯一的不同在‘*’操作上。環在乘特性處只滿足結合律，也就是說他沒有乘操作中性元素和逆元素，也不滿足交換律。

　　整數是一個典型的環。

　　線性函式，

　　假設V，W 是兩個關於域K(注：沒有特殊說明本講義的體是實數)的向量空間，一個對映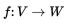叫做線性對映(函式)。如果對於V中任意兩個元素x和y以及K中元素a，f 滿足下列條件：

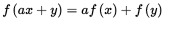
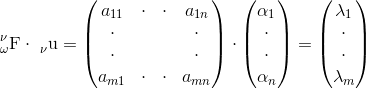
　　矩陣是向量空間的線性對映的一種表現形式。它是向量線性對映最佳表現形式。因此直到現在他還是研究多元性線性問題的一種主要手段。

　　矩陣的書寫：

　　其中(a11 a12 ... a1n)... (am1 am2 ... amn)是行向量,(a11 a21 ... am1) ... (a1n a2n ... amn)列向量。

　　矩陣的加減乘：

　　+：

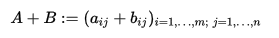
　　例：

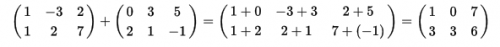
　　例：

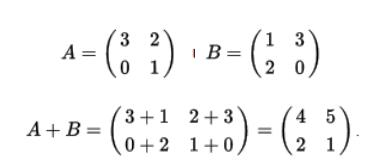
　　減法和加法沒有任何區別。因為A-B=A +(-B)

　　其它矩陣“+”操作：

　　*：

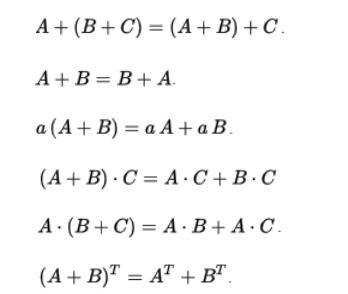
　　1. 與標量相乘

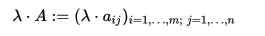
　　例子

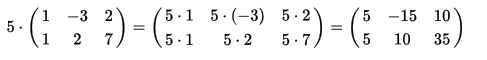
　　2. 矩陣相乘：

　　假設A,B,C是三個矩陣，且A*B=C。則下列等式滿足：

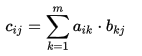
　　通過這個等式我們可以確定整個矩陣C的元素。

　　例：

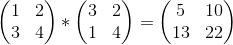
　　例：

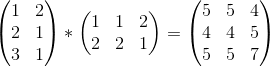
　　通常

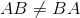
　　常用的乘操作公式：

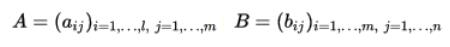以及是三個矩陣，那麼下列等式總是有效。

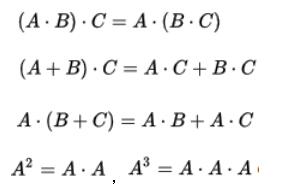
　　矩陣轉置

　　簡單表示法

　　一般表示法：

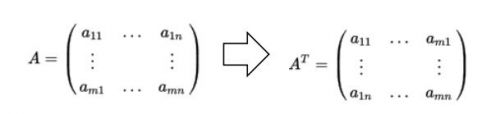
　　其它與轉置矩陣有關的公式：

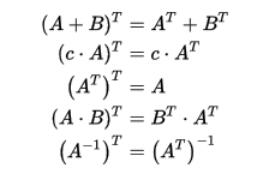
　　逆矩陣

　　一個實數平方矩陣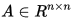叫正則矩陣如果存在一個矩陣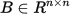滿足下列等式：

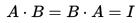
　　其中I是單位矩陣。矩陣B是唯一確定，並被稱為A的逆矩陣。A的逆矩陣通常用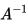來表示。

　　逆矩陣常見的性質：

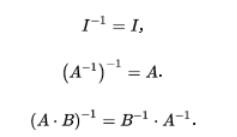
　　(通過這個公式，人們可以把難以求逆的矩陣分解成容易求逆的矩陣)

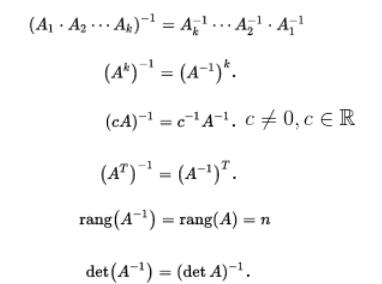
　　逆矩陣的確定：高斯-約旦演算法

　　例子：

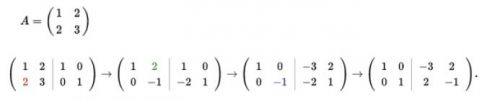
　　例子：

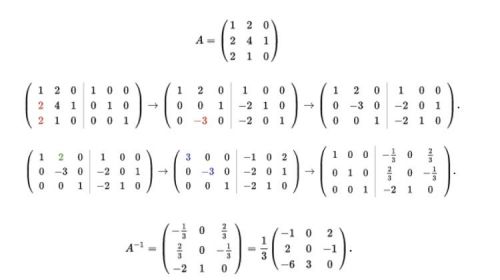
　　逆矩陣的確定：行列式法

　　逆矩陣的確定：特徵多項式法：

　　(選學)矩陣和線性函式的關係

　　假設K是一個域，V 和 W 是兩個有窮維向量空間，分別帶有維數n和m。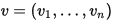和是V和W的基底。這兩個向量空間能分別與標準座標空間Kn和Km同構，這是因為對於任意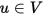都可以用下面唯一的等式表達：

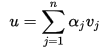
　　等式的右邊可以立馬寫成列座標的形式：

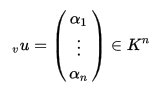
　　通過上面的等式，我們能容易地證明V和W與Kn和Km同構(一一對映並且是線性的)。

　　假設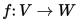是一個線性對映，那麼V的一個基底向量的象可以用下面的等式來表達：

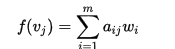
　　同樣等式的右邊也可以寫成座標的形式:

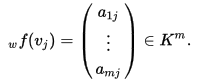
　　我們把每次求出的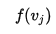排成一排,組成下面的一個矩陣.

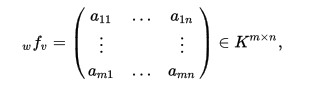
　　我們也叫他對映矩陣.

　　下面我們來證實上面對映矩陣的構成是合理的。

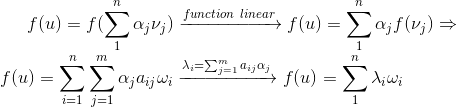
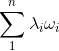　　又可以寫成座標的形式:

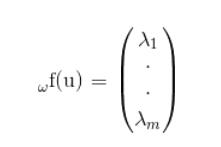
　　觀察(*)等式，我們可以立即把等式寫成矩陣和向量相乘的形式。