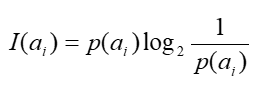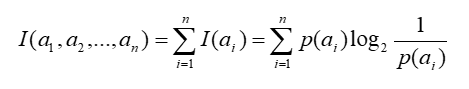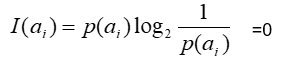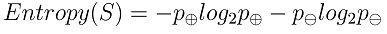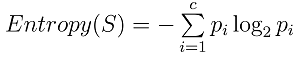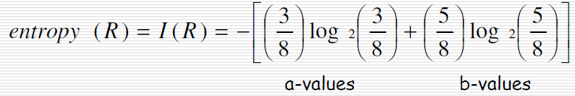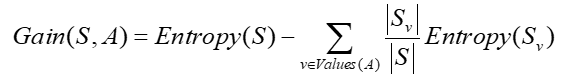分類

分類（Classification）任務就是通過學習獲得一個目標函式（Target Function）f, 將每個屬性集x對映到一個預先定義好的類標號y。

分類任務的輸入資料是記錄的集合，每條記錄也稱為例項或者樣例。用元組(X,y)表示，其中，X 是屬性集合，y是一個特殊的屬性，指出樣例的類標號（也稱為分類屬性或者目標屬性）。

解決分類問題的一般方法

分類技術是一種根據輸入資料集建立分類模型的系統方法。

分類技術一般是用一種學習演算法確定分類模型，該模型可以很好地擬合輸入資料中類標號和屬性集之間的聯絡。學習演算法得到的模型不僅要很好擬合輸入資料，還要能夠正確地預測未知樣本的類標號。因此，訓練演算法的主要目標就是要建立具有很好的泛化能力模型，即建立能夠準確地預測未知樣本類標號的模型。

分類方法的例項包括：決策樹分類法、基於規則的分類法、神經網路、支援向量機、樸素貝葉斯分類方法等。

通過以上對分類問題一般方法的描述，可以看出分類問題一般包括兩個步驟：

1. 模型構建（歸納）
   通過對訓練集合的歸納，建立分類模型。

2. 預測應用（推論）
   根據建立的分類模型，對測試集合進行測試。

決策樹

決策樹是一種典型的分類方法，首先對資料進行處理，利用歸納演算法生成可讀的規則和決策樹，然後使用決策對新資料進行分析。本質上決策樹是通過一系列規則對資料進行分類的過程。

決策樹的優點

1. 推理過程容易理解，決策推理過程可以表示成If Then形式；
2. 推理過程完全依賴於屬性變數的取值特點；
3. 可自動忽略目標變數沒有貢獻的屬性變數，也為判斷屬性變數的重要性，減少變數的數目提供參考。

決策樹演算法

與決策樹相關的重要演算法：CLS, ID3，C4.5，CART

1. Hunt,Marin和Stone 於1966年研製的CLS學習系統，用於學習單個概念。
2. 1979年, J.R. Quinlan 給出ID3演算法，並在1983年和1986年對ID3
   進行了總結和簡化，使其成為決策樹學習演算法的典型。
3. Schlimmer和Fisher於1986年對ID3進行改造，在每個可能的決策樹節點建立緩衝區，使決策樹可以遞增式生成，得到ID4演算法。
4. 1988年，Utgoff 在ID4基礎上提出了ID5學習演算法，進一步提高了效率。 1993年，Quinlan
   進一步發展了ID3演算法，改進成C4.5演算法。
5. 另一類決策樹演算法為CART，與C4.5不同的是，CART的決策樹由二元邏輯問題生成，每個樹節點只有兩個分枝，分別包括學習例項的正例與反例。

決策樹的表示

決策樹的基本組成部分：決策結點、分支和葉子。

決策樹中最上面的結點稱為根結點，是整個決策樹的開始。每個分支是一個新的決策結點，或者是樹的葉子。每個決策結點代表一個問題或者決策.通常對應待分類物件的屬性。每個葉結點代表一種可能的分類結果。

在沿著決策樹從上到下的遍歷過程中，在每個結點都有一個測試。對每個結點上問題的不同測試輸出導致不同的分枝，最後會達到一個葉子結點。這一過程就是利用決策樹進行分類的過程，利用若干個變數來判斷屬性的類別。

ID3

ID3演算法主要針對屬性選擇問題。是決策樹學習方法中最具影響和最為典型的演算法。

該方法使用資訊增益度選擇測試屬性。

• 資訊量大小的度量

Shannon1948年提出的資訊理論理論。事件ai的資訊量I(ai )可如下度量：

其中p(ai)表示事件ai發生的概率。

假設有n個互不相容的事件a1,a2,a3,….,an,它們中有且僅有一個發生，則其平均的資訊量可如下度量：

由上式，對數底數可以為任何數，不同的取值對應了熵的不同單位。

通常取2，並規定當p(ai)=0時：

• 熵

用熵度量樣例的均一性

熵刻畫了任意樣例集合 S 的純度

給定包含關於某個目標概念的正反樣例的樣例集S，那麼 S 相對這個布林型分類（函式）的熵為：

資訊理論中對熵的一種解釋：熵確定了要編碼集合S中任意成員的分類所需要的最少二進位制位數；熵值越大，需要的位數越多。

更一般地，如果目標屬性具有c個不同的值，那麼 S 相對於c個狀態的分類的熵定義為：

例如：求集合R = {a,a,a,b,b,b,b,b}的資訊熵

理解資訊熵：

1. 資訊熵是用來衡量一個隨機變量出現的期望值，一個變數的資訊熵越大，那麼它出現的各種情況也就越多，也就是包含的內容多，我們要描述它就需要付出更多的表達才可以，也就是需要更多的資訊才能確定這個變數。
2. 資訊熵是隨機變數的期望。度量資訊的不確定程度。資訊的熵越大，資訊就越不容易搞清楚（雜亂）。
3. 一個系統越是有序，資訊熵就越低；反之，一個系統越是混亂，資訊熵就越高。資訊熵也可以說是系統有序化程度的一個度量。
4. 資訊熵用以表示一個事物的非確定性，如果該事物的非確定性越高，你的好奇心越重，該事物的資訊熵就越高。
5. 熵是整個系統的平均訊息量。 資訊熵是資訊理論中用於度量資訊量的一個概念。一個系統越是有序，資訊熵就越低；反之，一個系統越是混亂，資訊熵就越高。
6. 處理資訊就是為了把資訊搞清楚，實質上就是要想辦法讓資訊熵變小。

• 資訊增益

用來衡量給定的屬性區分訓練樣例的能力

ID3演算法在生成 樹的每一步使用資訊增益從候選屬性中選擇屬性

用資訊增益度量熵的降低程度

屬性A 的資訊增益，使用屬性A分割樣例集合S 而導致的熵的降低程度

Gain (S, A)是在知道屬性A的值後可以節省的二進位制位數

資訊增益代表了在一個條件下，資訊複雜度（不確定性）減少的程度。

理解資訊增益：

熵：表示隨機變數的不確定性。
條件熵：在一個條件下，隨機變數的不確定性。
資訊增益：熵 - 條件熵。表示在一個條件下，資訊不確定性減少的程度。
例如：
假設X(明天下雨)的資訊熵為2（不確定明天是否下雨），Y(如果是陰天則下雨）的條件熵為0.01（因為如果是陰天就下雨的概率很大，資訊就少了） 資訊增益=2-0.01=1.99。資訊增益很大。說明在獲得陰天這個資訊後，明天是否下雨的資訊不確定性減少了1.99，所以資訊增益大。也就是說陰天這個資訊對下雨來說是很重要的。

ID3 決策樹建立演算法

1. 決定分類屬性
2. 對目前的資料表，建立一個節點N
3. 如果資料庫中的資料都屬於同一個類，N就是樹葉，在樹葉上標出所屬的類
4. 如果資料表中沒有其他屬性可以考慮，則N也是樹葉，按照少數服從多數的原則在樹葉上標出所屬類別
5. 否則，根據平均資訊期望值E或GAIN值選出一個最佳屬性作為節點N的測試屬性
6. 節點屬性選定後，對於該屬性中的每個值：
   從N生成一個分支，並將資料表中與該分支有關的資料收集形成分支節點的資料表，在表中刪除節點屬性那一欄如果分支資料表非空，則運用以上演算法從該節點建立子樹。

小結
ID3演算法是一種經典的決策樹學習演算法，由Quinlan於1979年提出。ID3演算法的基本思想是，以資訊熵為度量，用於決策樹節點的屬性選擇，每次優先選取資訊量最多的屬性，亦即能使熵值變為最小的屬性，以構造一顆熵值下降最快的決策樹，到葉子節點處的熵值為0。此時，每個葉子節點對應的例項集中的例項屬於同一類。

R語言中的決策樹實現

• 安裝資料包

安裝rpart、rpart.plot、rattle三個資料包
rpart:用於分類與迴歸分析
rpart.plot：用於繪製資料模型
rattle:提供R語言資料探勘圖形介面
安裝語句：

rpart:install.packages("rpart")
rpart:install.packages("rpart.plot")
install.packages("rattle")

• 步驟1：生成訓練集和測試集

以iris資料集為例：
訓練集：

iris.train=iris[2*(1:75)-1,] 
返回原資料集1、3、5、7、8、......、149奇數行行所有列的資料

測試集：

iris.test= iris[2*(1:75),] 
返回原資料集2、4、6、8、10、......、150偶數行所有列的資料

• 步驟2：生成決策樹模型

載入rpart包：

> library("rpart")

> model <- rpart(Species ~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, data = iris.train,  method="class")

rpart引數解釋：

rpart(formula, data, method, parms, …)

1. ormula是迴歸方程的形式，y~x1+x2+…，
   iris一共有5個變數，因變數是Species,自變數是其餘四個變數，所以formula可以省略為Species~.
2. data是所要學習的資料集
3. method根據因變數的資料型別有如下幾種選擇：anova（連續型），poisson（計數型），class（離散型），exp（生存型），因為我們的因變數是花的種類，屬於離散型，所以method選擇class
4. parms可以設定純度的度量方法，有gini（預設）和information（資訊增益）兩種。

• 步驟3：繪製決策樹

rpart.plot(model)

或

fancyRpartPlot(model)

• 步驟4：對測試集進行預測

iris.rp3=predict(model, iris.test[,-5], type="class") 

iris.test[,-5]的意思是去掉原測試集第5列後的資料

• 步驟5：檢視預測結果並對結果進行分析，計算出該決策樹的accuracy（分類正確的樣本數除以總樣本數）

table(iris.test[,5],iris.rp3) 

可得accuracy=（25+24+22）/75=94.67%

• 步驟6：生成規則

asRules(model)